Оптимизация документопотоков в АСУ. Применение метода частично-целочисленного линейного программирования(АОИ)

1.Математическая постановка задачи составления титульного списка

Критерий отбора задач:

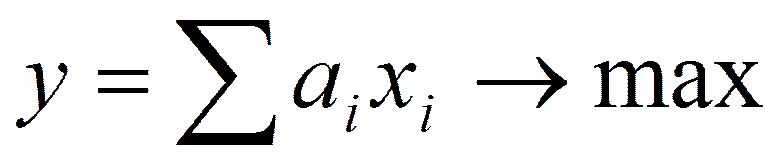
a_i – эффективность применения задачи

x_i = 0 1; 0 – задача не используется, 1 – используется.

Ограничения: 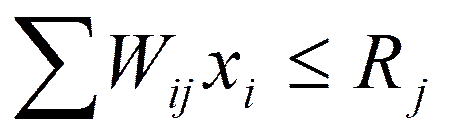, где - j-ый ресурс; 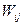- расход j-ого ресурса на i-ую задачу

2. Задача эффективного распределения задач по подсистемам АСУ

Критерий:

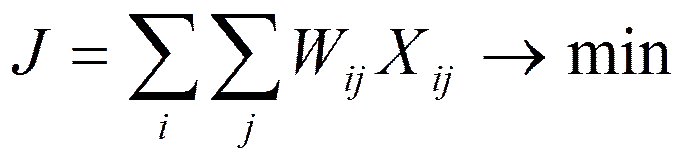, где i – задача, j – подсистема

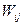- затраты на реализацию i-ой задачи в j-ой подсистеме

Ограничения:

Каждая задача должна решаться только в одной подсистеме

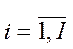, , I – число задач

Ограничение на затраты 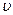- ого ресурса в j-ой подсистеме

,

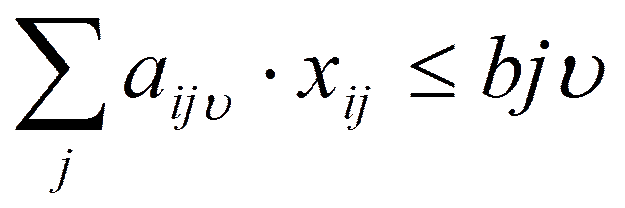3. Оптимизация документопотоков в АСУ

Введем переменные:

- число документов, передаваемых из i-ого подразделения в j-ое, подготовленных k –ым способом и отправленных 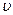-ым способом.

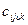- стоимость передачи одного документа.

a_i – число документов, которые должны быть подготовлены в i-ом подразделении.

b_j – число документов, которые должны быть приняты в j-ом подразделении.

c_k – число документов, которые могут быть подготовлены k-ым способом.

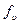- число документов, которые могут быть переданы 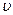-ым способом.

Целевая функция:

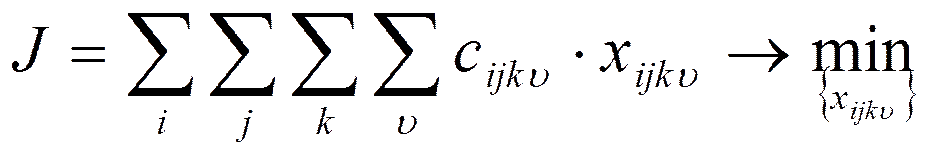
Ограничения:

Сумма документов, которые готовятся в i-ом подразделении, равна a_i

Сумма документов, которые приняты в j-ом подразделении, равна b_j

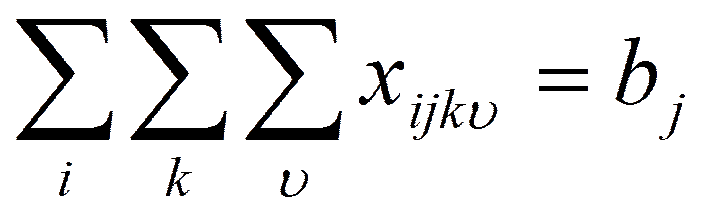
Ограничения на возможность подготовки данных

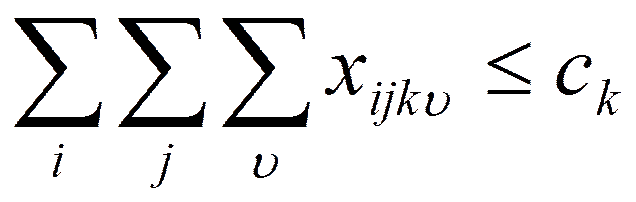
Ограничения по передаче данных

Производственные ограничения

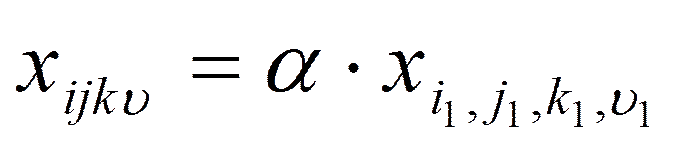
Все эти задачи частично целочисленного линейного программирования, т.к. имеются неравенства

Решение задачи частично (полностью) целочисленного линейного программирования

Метод отсекающих плоскостей Гомори 2-ого рода

Решение исходной задачи без дополнительных условий

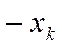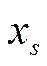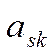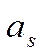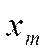z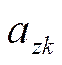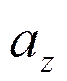

Среди переменных решения 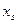, ищем переменную с наибольшей дробной долей. Пусть это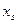

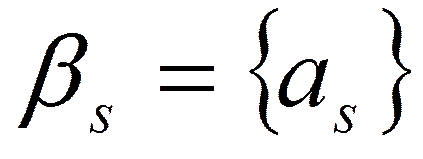
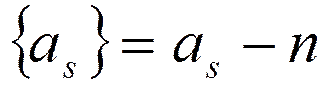- дробная доля, где n – целое число, не превышающее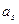

Строим строку отсечения:

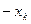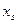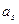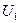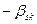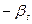z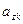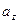

1) Если на переменную 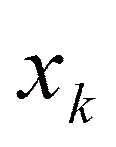не наложено условие целочисленности, то:

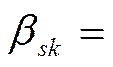
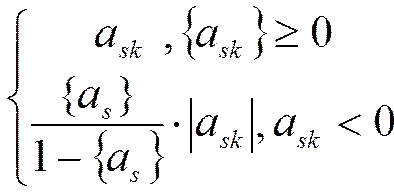
3) На 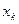наложено условие целочисленности:

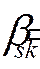
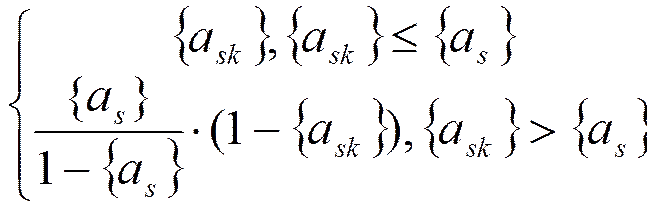
Пример:

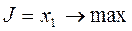
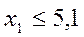
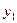		5,1
z	-1

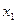		5,1
z		5,1

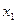		5,1
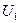	-1	-0,1
z		5,1

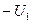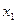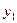	-1	0,1
z

Получаем x₁ = 5 – задача решена

Модификация представления отсечений

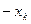		b

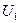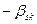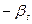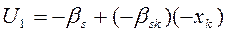
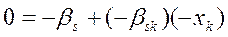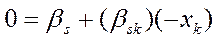-_U1

+U1

Заносим это равенство в Жорданову таблицу:

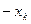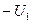			b
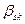		-1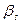

Далее имеем таблицу:

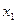		5,1
z		5,1

Строим таблицу отсечений:

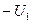		-1	0,1
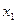			5,1
z			5,1

Переводим нули из базисных в свободные:

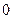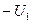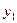		-1	0,1
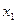z

Задача решена

Особенности решения задачи оптимизации документопотоков

Адаптация алгоритма решения к тождествам

Из-за того, что мы имеем много равенств, нули должны быть переведены из базисных в свободные.

1) В процессе преобразования жордановой таблицы появляются строки, соответствующие равенствам с отрицательными свободными членами, программа симплекс-метода отвечает "решения нет". Хотя достаточно справа и слева это уравнение умножить на (-1).

2) В процессе решения появляется строка, содержащая все нули, соответствующая равенству. Эту строку отбросить и продолжать решение дальше.

Пример:

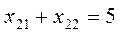
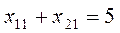
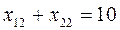
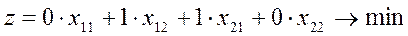
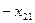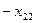					b
z

Переводим нули из базисных в свободные:

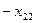		b
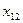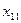	-1
z	-2	-15