Адаптивная обработка данных означает изменение алгоритмов обработки после получения информации об объекте изучения, на основе обработки этих данных или получение новых данных.

Адаптивная обработка данных означает изменение алгоритмов обработки после получения информации об объекте изучения, на основе обработки этих данных или получение новых данных.

В курсе должны быть решены два основных вопроса:

Какую информацию нужно извлечь из данных, чтобы алгоритм обработки стал оптимальным?

2. Формирование минимального объема информации (получение наиболее информативных параметров).

Повышение достоверности контроля состояния объекта управления (определение числа датчиков) на основе формулы Байеса(АОИ)

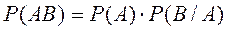P(AB)=P(B)*P(A/B) P(A)*P(B/A)= P(B)*P(A/B)

P(B/A)= {P(B)*P(A/B)} / P(A)

Объект может быть в одном из двух состояний:

Н₁ – объект работоспособен

Н₂ – объект не работоспособен

P(Н₁) = 0,7

P(Н₂) = 0,3

Имеются 2 датчика состояния объекта

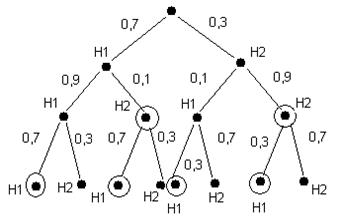
1-ый датчик дает правильные сведения об объекте с вероятностью 0,9, а ошибочные сведения соответственно с вероятностью 0,1

2-ой датчик дает правильные сведения с вероятностью 0,7, а ошибочные с вероятностью 0,3

Сообщение: 1-ый датчик сообщает, что объект не работоспособен, а 2-ой сообщает, что объект работоспособен.

Вероятностная диаграмма:

P(A) = 0,7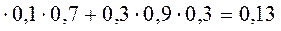

P(H₁/A) = 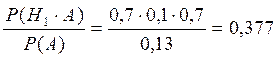- вероятность того, что объект работоспособен

P(H₂/A) = 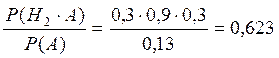- вероятность того, что объект неработоспособен

Прием решения ведется с вероятностью 0,95, поэтому на объект поставлен дополнительный датчик, который дает правильные сведения с вероятностью 0,9 , а ошибочные с вероятностью 0,1.

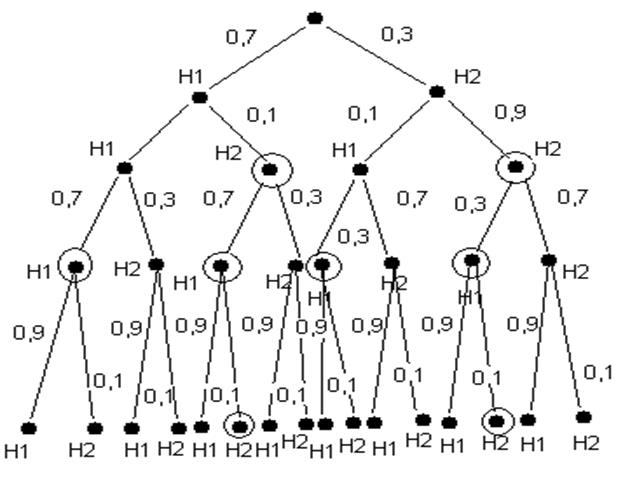Сообщение: 1-ый датчик – объект неработоспособен

2-ой датчик – объект работоспособен 3-ий датчик – объект неработоспособен

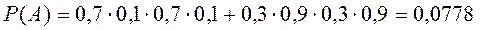
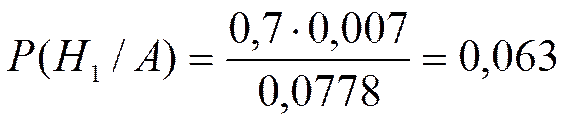
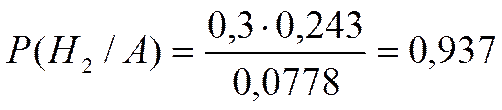
С вероятностью 0,937 можно сделать вывод, что объект неработоспособен

Решение вычислительных задач на однородном вычислительном комплексе

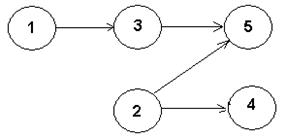
Необходимо решить данный комплекс задач за минимальное время с помощью минимального количества машин.

Имеем длительность каждой работы:

i
ti

Заданный граф превращается в сетевой график:

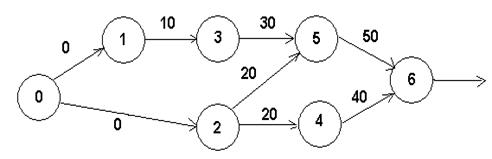
Наименьшее количество машин:

Мкр =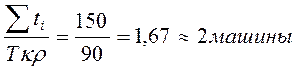

Обозначим t_i – время начала i-ой работы

Тогда система ограничений примет вид:

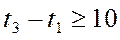
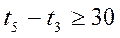
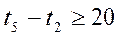
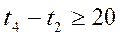
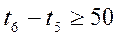
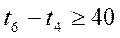
Критерий: J=t₆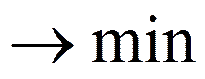

Получим:

t₁ = 0

t₂ = 20

t₃ = 10

t₄ = 50

t₅ = 40

t₆ = 90

Распределение задачи по свободным машинам желательно с учетом их взаимосвязи:

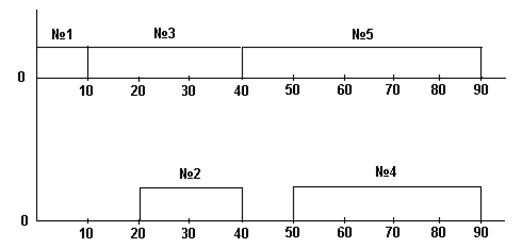
Решение календарных задач на неоднородном комплексе

Имеем детали Д1, Д2, Д3.

	Этапы обработки
Д1	B1	B2	B3
Д2	B4	B5	B6
Д3	B7	B8	B9

	Этапы обработки
Д1	3ст	1ст	5ст
Д2	5ст	4ст	1ст
Д3	1ст	3ст	2ст

Время обработки:

	Этапы обработки
Д1
Д2
Д3

В1 – 1-ая деталь обрабатывается на 3-ем станке.время обработки=5

Граф взаимосвязи работ:

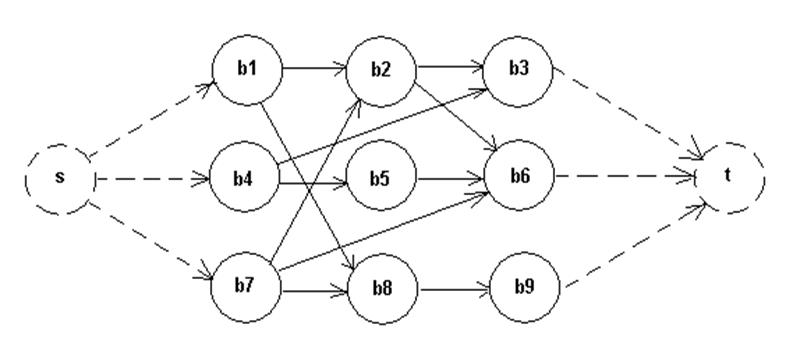
Сложная задача разбивается на части.

Решая задачу без декомпозиции (обычным симплекс методом). Заполняем Жорданову таблицу.

Разрешающие элементы: (2,1); (5,2); (7,3); (10,4); (4,1); (9,3).

Целевая функция: z_max=80.

Здесь происходит 360 вычислений.

Заполняем Жорданову таблицу

Разрешающие элементы: (1,1); (2,4).

Целевая функция: z_max=80

Здесь число вычислений равно 56.

Решение задачи частично (полностью) целочисленного линейного программирования

Задача решена

Особенности решения задачи оптимизации документопотоков

Моменты времени.(АОИ)

Задачи отличаются режимом обслуживания заявок.

Замкнутое СМО.

Дано:

n-кафедр,

m – ЭВМ,

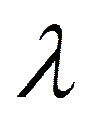- поток заявок,

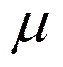- поток решений.

Кафедра, подавшая заявку не обслуживается до тех пор, пока не будет выполнена ее 1-ая заявка.

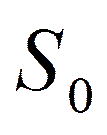- заявок нет, ЭВМ свободны, очереди нет.

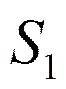-1-ая заявка, 1 ЭВМ занята, очереди нет.

…..

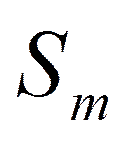- m заявок, m – ЭВМ, очереди нет.

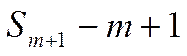заявка, , m – ЭВМ занято, 1 заявка в очереди.

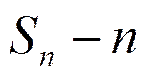заявок, m – ЭВМ занято, n-m в очереди.

Характеристики системы:

Определим среднее число заявок в системе -

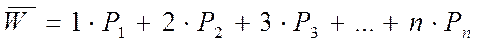
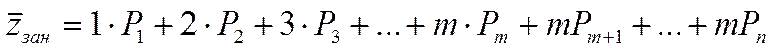
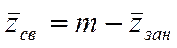- свободных.

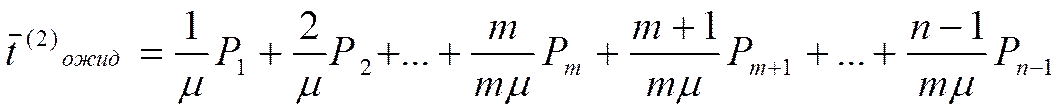
- время ожидания подачи второй заявки.

Среднее число заявок в очереди - .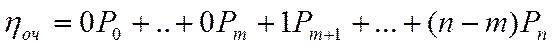

Выбор оптимального значения числа ЭВМ

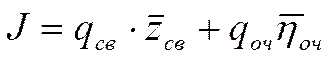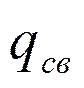, - потери, связанные с простоем машины; 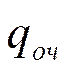- потери,связанные с простоем заявки в очереди.

**********************************************************************

X(t) Y(t)

K(t) – реакция на короткий импульс

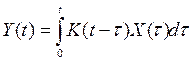
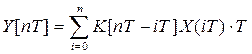(1)

1. Алгебраический метод восстановления сигнала(МОИ)

Представим уравнение (1) в матричной форме:

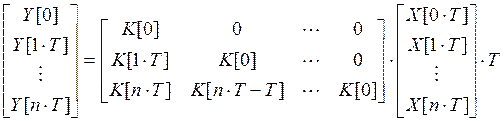
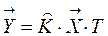
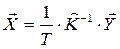
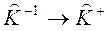
Если определитель матрицы равен 0, то применяем псевдообращение

Пример

W(p) =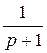

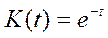
T=0,02

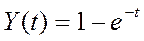
X(t) - ?

n	Y[n]	K[n]
	0,02	0,98
	0,04	0,96

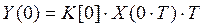
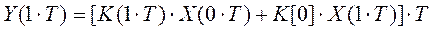
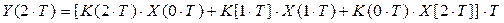
Из первого уравнения, зная Y и K, можем найти Х:

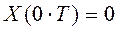
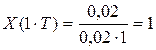
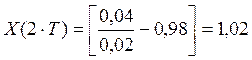
2. Восстановление входного сигнала во временной области на основе дифференциального уравнения(МОИ)

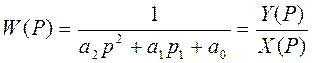
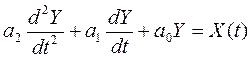(2)

Представим Y[t] в виде полинома:

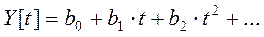
Если в это выражение подставить моменты времени t, то получим систему линейных уравнений

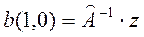
Далее находим b₀, b₁, b_{2 , …}

Найдя производные по t и, подставив их в уравнение (2), получим входной сигнал

Вместо полиномов можно использовать подходящие системы функций, для которых существуют производные : sinw_it, cosw_it ; БПФ (разложение в ряд Фурье).

Цель работы

Иследование метода позволяющего исключить динамические искажения, вибрации, вносимые измерительной системой. Ознакомление с возможностями использования метода в информационных системах и системах управления.

Теоретическая часть

Решение задачи восстановления входных сигналов сводится к решению интегрального уравнения вида

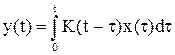, (1)

где К(t) – импульсная переходная функция стационарного оператора, x(t) – искомый входной сигнал. В большинстве случаев линейные операторы измерительных систем имеют интегрирующий характер [1,2].

Динамические характеристики восстанавливающих операторов, применяемых для преобразования сигнала y(t), приближаются к характеристикам неидеальных дифференцирующих операторов, имеющих укороченные по длине импульсные переходные функции. Входной сигнал может быть восстановлен по формуле:

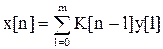. (2)

Если n изменяется в больших пределах, то вычисление по формуле (66) может оказаться очень трудоемкой операцией по числу операций сложения и умножения. Некоторое упрощение можно получить, если применить БПФ-свертку без двоичных инверсий. Однако импульсная переходная функция K[n] дифференцирующих звеньев принципиально не может быть реализована точно. Попытку избежать этой принципиальной нереализуемости K[n], а с ней и достигнув точного восстановления входного сигнала можно осуществить на основе итерационных процедур Ван-Циттерта [1]. Для уравнения (2) итерационная процедура может быть представлена в виде

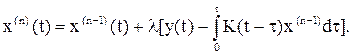(3)

Выбор величин l обеспечивается сходимостью в среднем к решению уравнения (1). В выражении (3) импульсная переходная функция принципиально может быть реализована с высокой точностью. Некоторого упрощения итерационной процедуры можно добиться, если, как и раньше в случае восстановления по формуле (2), применять БПФ-свертку без двоичных инверсий. Ниже приведены примеры применения БПФ-свертки для восстановления входного сигнала с помощью соотношения (2) путем перехода в частотную область и примеры восстановления входного сигнала на основе дискретизации соотношения (3).

Пример 1. Восстановление входного сигнала интегратора.

Входной сигнал в виде единичного скачка: X_i=1, где i= 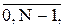N – число отсчетов. Для нашего примера N=16. Тогда на выходе интегратора будем иметь сигнал вида

Y^T=[ 0 1 2 3 4 5 6 7 8 9 10 0 0 0 0 0 ].

Дифференцирующий оператор

V^T=[ 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ].

Находим коэффициенты разложения в ряд Фурье для сигналов V и Y. Матрица дискретного преобразования Фурье имеет вид:

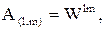где .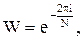

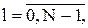
Для восстановления входного сигнала на интервале наблюдения необходимо наблюдаемый входной сигнал и дифференцирующий оператор дополнить соответствующим количеством нулей [3].

Коэффициенты разложения сигнала имеют вид: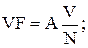

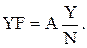
Тогда спектр восстановленного сигнала имеет вид: XF_j=VF_j·YF_j,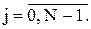

Применяя обратное преобразование Фурье, получаем 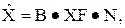где B_(l,m)=W^-lm.

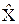=[ 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 ].

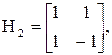
Для сокращения числа операций целесообразно применять БПФ, представленный в матричной форме. Матрица преобразований имеет вид:

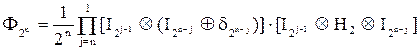, (4)

где I_n - единичная матрица размером (n ´ n), ÄA_j=A₁ÄA₂Ä…A_n - кронекеровское произведение, ÄA_i=A₁ÄA₂Ä…A_n - прямая сумма.

,

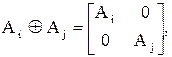
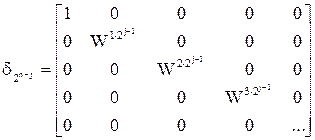где 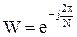, N = 2ⁿ - число отсчетов.

Формула (4) для n = 4 представляется в виде :

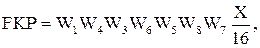(5)

где .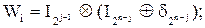

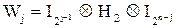i = 2,4,6,8 j = 1,3,5,7

Результаты представлены FKP с двоично-инверсными номерами. С помощью формул (4) и (5) находим спектр выходного сигнала и спектр восстанавливающего фильтра. Перемножаем их с двоично-инверсными номерами (не переставляя индексов). Входной сигнал находим по формуле

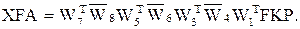(6)

Функции FKR в формулах (5) и (6) имеют двоично-инверсный порядок. Благодаря отсутствию операции с преобразованием индексов получим экономию в вычислительных операциях.

Пример 2. Восстановление входного сигнала интегрирующего звена 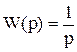с помощью итерационных процедур.

Дифференцирующие звенья принципиально не могут быть реализованы с большой точностью, интегрирующие инерционные звенья принципиально могут быть реализованы с любой заданной точностью. Для восстановления входного сигнала целесообразно использовать итерационную процедуру

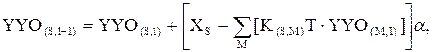(7)

где Т (шаг интегрирования) и a определяются точностью интегрирования, К – матрица преобразования интегрирующего оператора, S = 0…7, M = 0…7, I = 1…2000 (число итераций). За счет выбора малого значения a= 0,1 обеспечиваем сходимость итерационной процедуры.

Начальные значения входного сигнала принимаются равными выходному сигналу.

Входной сигнал: X^T = [1 2 3 4 3 2 1 1].

Выходной сигнал: Y^T = [0,1 0,3 0,6 1 1,3 1,5 1,6 1,7]. T=0,1, a=0,1.

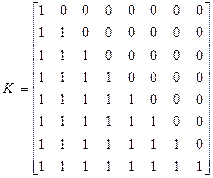
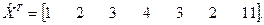
Пример 3. Восстановление входного сигнала апериодического звена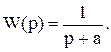

Для восстановления входного сигнала используем итерационную процедуру (71). Начальные значения входного сигнала принимаются равными выходному сигналу. Импульсная переходная функция рассчитывается по формуле K(t) = e^-t. Матрица преобразования имеет вид

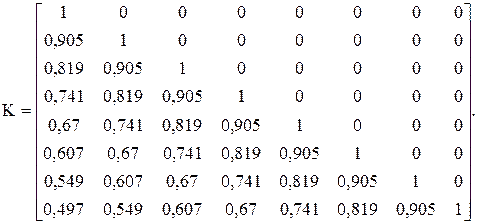
Входной сигнал Х^Т = [1 2 3 4 3 2 1 1].

Выходной сигнал: Y^T = [0,1 0,29 0,563 0,909 1,123 1,216 1,2 1,186]. T=0,1, a = 0,1.

Восстановленный входной сигнал после 2000-й итерации

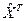= [1 2 3 4 3 2 1 1].

Порядок выполнения

1. Ознакомиться с содержанием работы, рассмотреть особенности изложенных в теоретической части примеров.

2. Используя команды операционной системы, получить доступ к программе выполнения лабораторной работы. (рис.1).

============================================

Лабораторная работа

"Итеративный метод восстановления сигнала

============================================

Теоритические сведения

Выход

============================================

Выберите пункт меню

Рис. 1. Меню лабораторной работы

3. Рассмотреть вопросы применения метода, изложенного в теоретической части, для конкретных моделей линейных динамических измерительных систем. Кратко это можно изложить так.

В данной лабораторной работе рассматривается итерационный метод восстановления, искаженного линейным оператором сигнала.

В качестве моделей линейной динамической измерительной системы приняты передаточные функции вида:

1. W(p)=1/p

2. W(p)=1/(p+a)

3. W(p)=1/p(p+a)

4. W(p)=1/(p+a1)(p+a2)

5. W(p)=1/(p+a)^2

6. W(p)=1/((p+h)^2+m^2)

с помощью которых могут быть описаны различные классы измерительных систем.

Итерационный процесс имеет вид:

Y(i+1)=Y(i)+(X-AY(i))a

где Х-выходной сигнал (сигнал после искажения)

А-матрица перехода линейного оператора (полученная с помощью одной из квадратурных формул; в данной работе применяется формула прямоугольника)

Y(0)=X

a-величина обеспечивающая сходимость итерационного процесса (в данной работе а=0.1)

Начиная с передаточной функции 3. диагональные элементы матрицы А равны 0 (т.е. в начальный момент времени), что не позволяет восстановить исходный сигнал.

В данной работе используется два метода решения этой проблемы.

1. Восстановление с псевдообращением: в матрице А срезается первая строка и

последний столбец (т.е. диагональные элементы становятся отличными от 0).

2. Восстановление с комб. фильтром: ко всем элементам матрицы А лежащим не выше главной диагонали прибавляется функция вида f(t)=k*exp[-nt] (в лабораторной работе используется функция f(t)=1*exp[-100t]), которая в начальный момент времени не равна 0, а в остальные стремится к 0.

Для ускорения процесса восстановления сигнала,свертку А на Y(i) можно выполнять используя быстрые преобразования (в лабораторной работе используется алгоритм БПФ).

Рассмотрим суть метода:

Ф(2^n)=(1/(2^n))П[I(2^(j-1))*(I(2^(n-j))+b(2^(n-j))][I(2^(j-1))*H2*I(2^(n-j))]

где *-кронекеровское произведение

+-прямая сумма

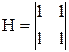П-произведение от j=n до 1

b(2^(n-j))=диаг.{1,W^(1·2^(j-1)),W^(2·2^(j-1)),W^(3·2^(j-1)),...}

W=exp(-j2п/8)

Для N=8 (n=3) имеем:

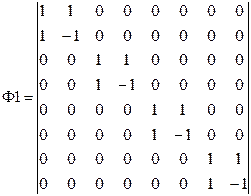
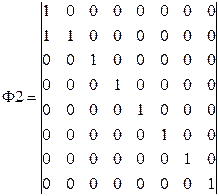
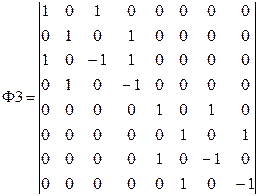
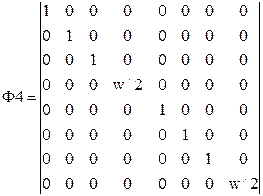
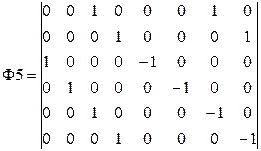
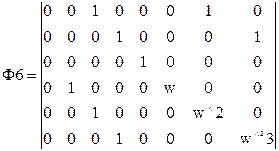
Ф·f=(1/8)·Ф2·Ф1·Ф4·Ф3·Ф6·Ф5·f

F1=(1/8)·Ф·[первый столбец матрицы А]-спектр матрицы перехода

F2=(1/8)·Ф·[Y(i)]-спектр восстанавливаемого сигнала

F=F1·F2

Следовательно свертка, применяя обратное преобразование Фурье, равна

f=F·Ф5°·Ф6°·Ф3°·Ф4°·Ф1°·Ф2°,где °-знак транспонирования.

Затем результат подставляется в основную формулу итеративного метода:

Y(i+1)=Y(i)+(X-AY(i))a

Примечание: в результате БПФ результат получается в двоичном инверсном коде в несортированном виде, но в данной лабораторной работе в результате многократного применения БПФ и использования обратного БПФ результат получается в виде пригодном для дальнейшего использования, т.е. не требуется производить сортировку и переводить инверсный двоичный код в прямой.

Содержание отчета

1 Цель работы и основные теоретические положения.

2 Результаты восстановления искаженного сигнала для различных измерительных систем. Оценка эффективности метода.

3 Изложить возможности использования метода в информационных системах и системах управления.

Библиографический список

1. Клейман Е.Г. Идентификация входных сигналов в динамических системах// АиТ. 1999. №12. С. 3-15.

2. Аш Ж. И др. Датчики измерительных систем. В 2-х книгах. Кн.2: Пер с франц. М.: Мир, 1992. С. 292.

3. Василенко Г.И. Теория восстановления сигналов: от редукции к идеальному прибору в физике и технике. М., 1979. 272 с.

1.Оперативное оценивание параметров модели регрессии

при наличии аномальных результатов измерений(МОИ+АОИ)

В реальных системах обработки информации оценки 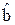вектора регрессионных коэффициентов b для модели

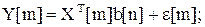
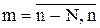, (38)

где X[m] – вектор наблюдаемых линейно независимых факторов;

b – вектор неизвестных и подлежащих оценке параметров;

e[m] – помеха типа белого шума, приходится проводить в условиях аномальных измерений (АИ) Y(l), l Î ( ).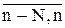

Наибольшее распространение при решении поставленной задачи получили метод максимального правдоподобия при известном законе распределения ошибки [10] и метод наименьших модулей (МНМ), обеспечивающий устойчивое решение в условиях отклонения реального закона распределения ошибки от постулируемого априори закона распределения [11,12]. Однако все эти методы требуют в случае обнаружения АИ значительных вычислительных затрат для исключения влияния самих измерений на искомую регрессионную зависимость.

Необходимо организовать процесс вычислений таким образом, чтобы не получать каждый раз результат заново, а корректировать процесс вычислений с учетом аномальности результата измерений. Подобный подход можно применять для обработки как накопленных данных, так и последовательно поступающей порции информации.

4.1. Метод выделения результата АИ

В основу его алгоритма положен итеративный метод решения на основе МНМ [11,13]. При этом оценка 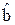, полученная на основе N результатов измерения, имеет вид

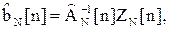(39)

где

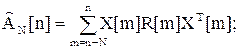(40)

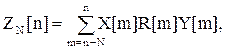(41)

где 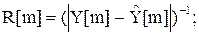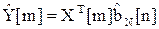- оценка m-го измерения выходного сигнала.

Начальные значения R[m]=1; 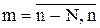соответствуют определению параметров 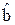по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (39) – (41) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[l] указывает на наиболее грубое l-измерение.

4.2. Рекуррентная процедура исключения АИ

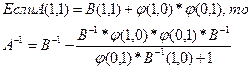
Матрицу 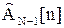и вектор Z_n-1[n] при R[m]=1; 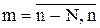можно определить из 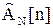, Z_N[n], полученных на первой итерации, путем исключения аномальных составляющих

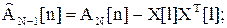(42)

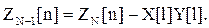(43)

На основании леммы об обращении матриц можно записать

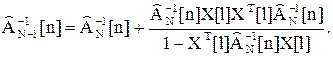(44)

Используя выражения (43) и (44), получаем

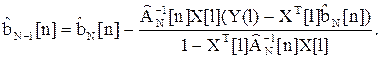(45)

Критерии оптимизации.

1. Минимизация следа матрицы -это сумма диагональных элементов матрицы .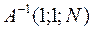

2. Максимизация определителя .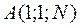

3. Независимое определение параметра .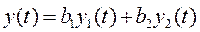

Рассмотрим на примере.

Для определения 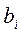входной сигнал 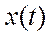выбирается так, чтобы

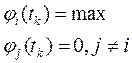
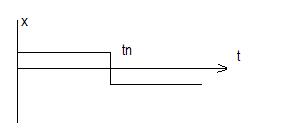
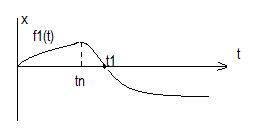
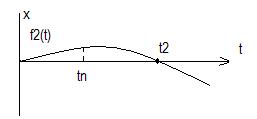
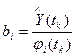
Поиск оптимального значения соответствующего критерия осуществляется на основе минимизации функции многих переменных.

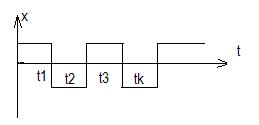
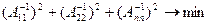, подбирая 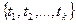при наличии линейных ограничений :

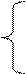
Качественное описание необходимости планирования эксперимент

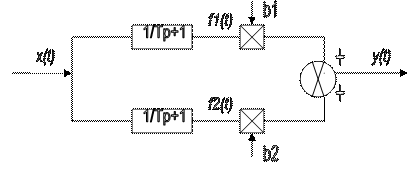
Связь между входным и выходным сигналом :

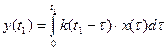
Подаем на вход единичный скачок x(t)=1(t) на выходе получим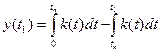

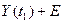- коэффициент влияния помехи будет большим.

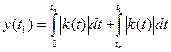
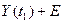-малое влияние помехи.

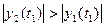
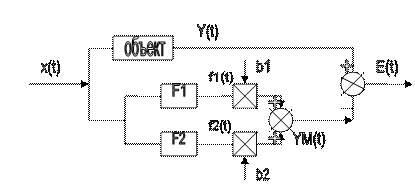
Замкнутый метод идентификации динамического объекта на основе градиентного метода.

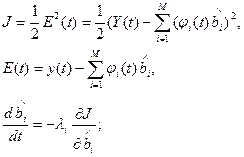
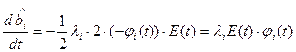
Свойства частот

При любом числе n - большом или малой справедливы следующие соотношения.

1. Правило сложения частот для несовместимых событий.

С = А + В;

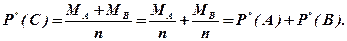(1.18)

2. Правило умножения частот для двух событий.

D = AB;

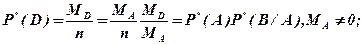
или

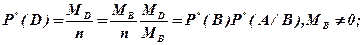
Полученные формулы

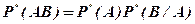(1.19)

или

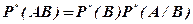(1.20)

имеют очень большое значение. Они показывают, что от одновременного появления двух событий А и В можно перейти к последовательности появления событий: вначале, например, наступает А, а затем - В, при условии, что событие А произошло. Таким образом, с помощью формул осуществляется переход к методу последовательных испытаний. Метод прост, нагляден, позволяет более осмысленно решать сложные вероятностные задачи.

Правило умножения вероятностей легко обобщается на случай произвольного числа событий

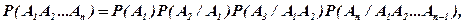(1.21)

т.е. вероятность произведения нескольких событий равна произведение вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место. Для независимых событий формула (1.21) перепишется в виде

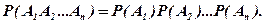(1.22)

Следует подчеркнуть, что, если имеется несколько событий А₁, А₂,…, A_n, то их попарная независимость 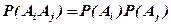еще не означает их независимости в совокупности.

Пример 1.6. В урне 7 шаров: 4 белых и 3 черных. Из нее выни­маются (одновременно или последовательно) два шара. Найти вероят­ность того, что оба они будут белыми. Интересующее событие А = два белых шара.

Решение. Рассмотрим следующие два события: первое - вынима­ние первого шара, второе - вынимание второго шара, при условии, что первый шар вынут из урны. Исходы этих испытаний обозначим d (вынут белый шар) и i (вынут черный шар). Соответствующее про­странство исходов Wизображено на рис.1.3.

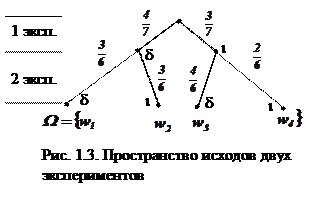
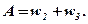
Используя формулы (1.9) и (1.19), (1.20), получаем

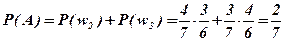
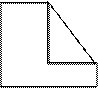
Таким образом, для подсчета вероятностей при проведении экспериментальных исследований основными являются теоретико-множественный и частотный методы. В связи с этим рассмотрим алгоритм подсчета вероятности попадания точки в выпуклую область. Любую невыпуклую область можно представить в виде совокупности выпуклых областей. Например, задана невыпуклая область D (рис.1.4). Эту область можно дополнить до выпуклой добавлением следующей области F, которая является выпуклой. Совокупную область назовем G. Тогда задача сведется к нахождению вероятности попадания в область G и непопадания в область F.Возможен другой подход-разбиение исходной области на выпуклые подмножества.

	D

	F
		G

Рис.1.4. Представление невыпуклой области совокупностью выпуклых областей

Наиболее простым и удобным для практики в описании выпуклых множеств является задание системой линейных неравенств.

ИЗ ”МОИ”:

Алгоритм

1. В правой части (то есть в матрице Т₂¹) находится основной столбец – тот столбец, в котором есть положительные элементы.

2. Ищем допустимые пары строк – это пары строк, пересекающие основной столбец по элементам с разными знаками.

3. Среди допустимых пар ищем уравновешенные пары. Для этого в матрице Т₁¹ нужно найти столбцы (столбец), пересекающие допустимую пару по нулевым элементам. И не существует строк, пересекающих подобные столбцы по нулевым элементам.

4. Формируем матрицу Т².

В рассматриваемом примере в качестве основного столбца берём крайний слева, то есть первый. 1-ая и 3-я строки – допустимая, уравновешенная пара.

Правило формирования Т²

Выписываются строки, пересекающие основной столбец по отрицательным элементам и нулям в любой последовательности, и выписывается строка равновесия. Строка равновесия формируется из уравновешенных пар путем умножения их на положительные коэффициенты такие, что на месте основного столбца получается нуль. Для повышения точности желательно все расчеты проводить в целых числах.

Основной столбец наделяется свойствами столбцов матрицы Т¹. Элементы основного столбца, отличные от нуля, заменяются на «-1».

В данном примере складываем первую и третью строки, в результате получаем матрицу Т²:

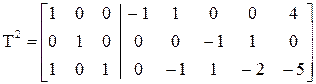
5. Для формирования матрицы Т³ будем искать в матрице Т² основной столбец (в примере это 2-ой столбец), допустимые пары (1-ая и 3-я строки). Эта же пара и уравновешенная.

6. Выписываем строки, пересекающие основной столбец по отрицательным элементам и нулям, а строку равновесия с единичными коэффициентами.

В примере поскольку основной столбец пересекает по отрицательному элементу 3-ю строку, то эту третью строку в матрице Т³ записываем на первое место. Вторую строку оставляем без изменений, а первую и третью строки складываем и записываем результат на место третьей строки:

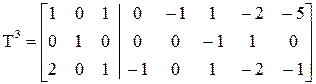
Здесь пятый столбец лишний, поэтому он исключается.

7. Формируем матрицу Т⁴: основной столбец третий.

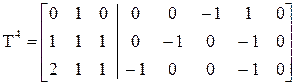
Допустимые, уравновешенные пары: 1,3 и 1,2.

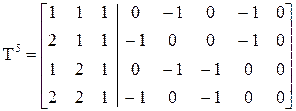
Выбрать основной столбец невозможно, строго положительного

столбца нет, значит, выписываем решение.

Решение системы можно представить в виде:

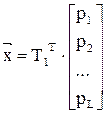, где L – число строк последней матрицы,

р_i ≥ 0.

Для примера решение будет иметь вид:

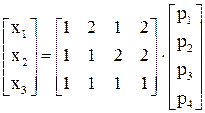
Решение можно представить в виде системы (в скалярной форме):

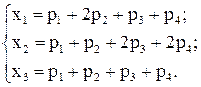
При р₁ = 1, р₂ = 1, р₃ = 1 и р₄ = 1 получим х₁ = 6, х₂ = 6, х₃ = 4.

При данных ограничениях х_i эта система выполняется.

Далее выражения для х_i подставляются в целевую функцию, а в качестве ограничения берется уравнение x_n+1=1. Затем находится решение полученной системы.

УСТОЙЧИВЫЕ АДАПТИВНЫЕ МЕТОДЫ ОЦЕНИВАНИЯ параметров НА ОСНОВЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.(АОИ)

Использование методов математической статистики позволяет находить по результатам выборочных измерений оценки искомых параметров математического ожидания, дисперсии и других числовых характеристик случайных величин.

Однако, поскольку оценки искомых параметров являются случайными величинами, то нельзя точно указать величину ошибки в определении этих параметров. Но если известен закон распределения результатов измерений, то оказывается, возможным сделать по этой ошибке суждения вероятностного характера, например, оценить доверительный интервал, который «накрывает» с известной вероятностью Р неизвестное истинное значение искомого параметра .Но знание интервала не увеличивает точность оценок, хотя и является важной дополнительной информацией. Для этого необходимо применять специальные методы. Одним из таких методов является метод максимального правдоподобия, основанный на предположении, что известен закон распределения измеряемых случайных величин, зависящий от искомых параметров.

И перейти к шагу 2.

Шаг 2

Минимизировать f(x_k + ld_k) при условии 0 £ l £ l_max ,

где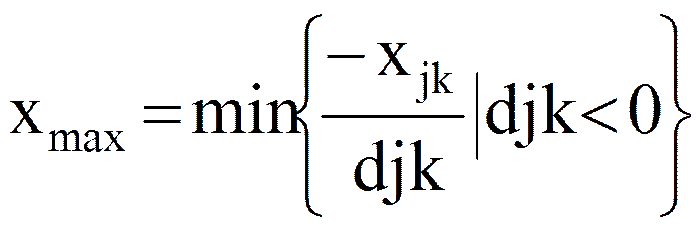

Пусть l_k - оптимальное решение этой задачи.

Положить

x_k+1 = x_k + l_kd_k,

(заменить k на k+1,т.е.задать новые начальные условия поиска)

И перейти к шагу 1.

Пример

Минимизировать

I = 2x₁² + 2x₂² – 2x₁x₂ – 4x₁ – 6x₂

Наши рекомендации