Доказательство эквивалентности систем (8) и (26).

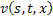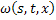Покажем, что если решением системы уравнений (26) являются непрерывно-дифференцируемые и ограниченные вместе со своими первыми производными функции и , то функции 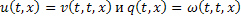, будут решением задачи Коши (8), (2), (9) при 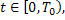где .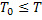

Продифференцируем (22) по :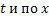

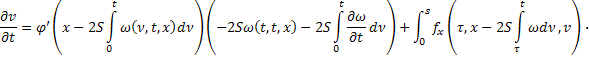
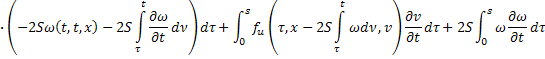
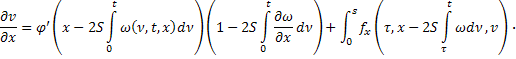
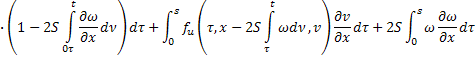
Умножим второе равенство на :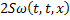

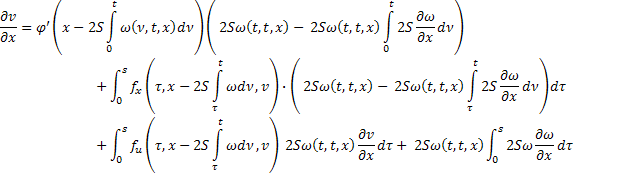
Получившееся равенство сложим с первым:

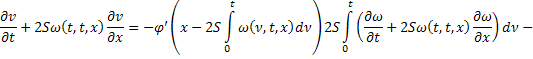
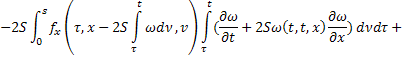
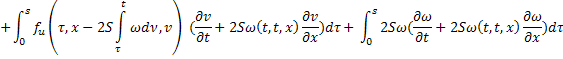
Обозначим через 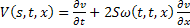, а через 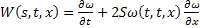тогда последнее равенство перепишется в виде:

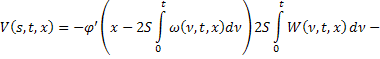
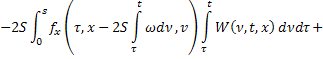
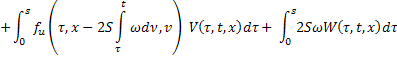
Аналогично продифференцируем (23) по :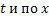

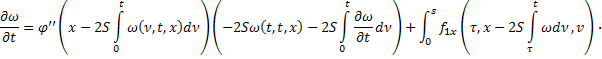
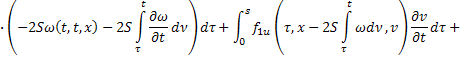
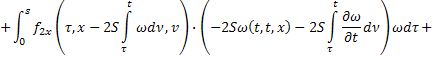
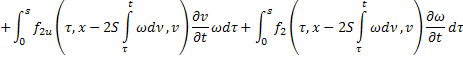
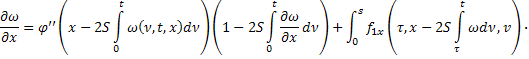
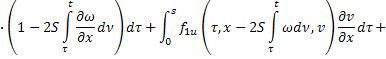
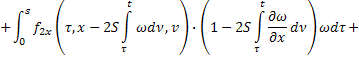
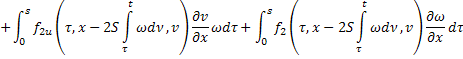
Умножим второе равенство на :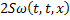

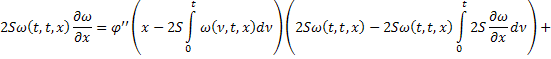
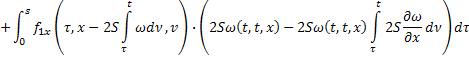
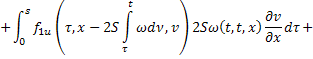
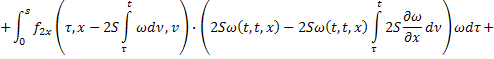
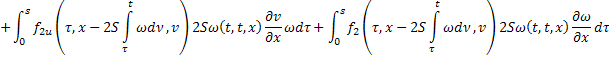
Сложим получившееся равенство с первым:

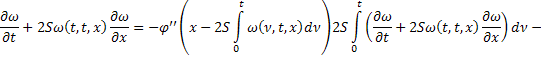
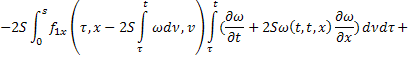
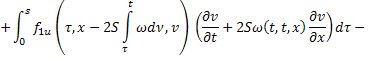
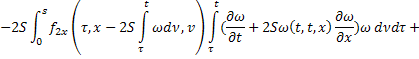
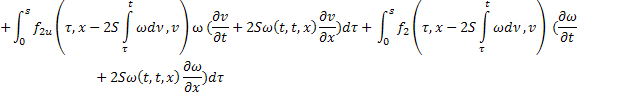
Последнее равенство с учётом обозначений 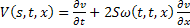, 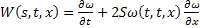перепишем в виде:

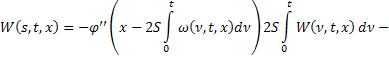
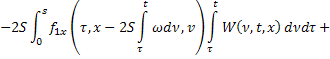
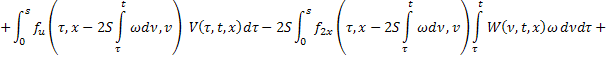
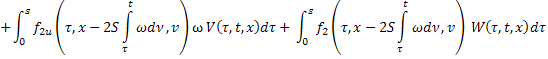
Итак, получили два уравнения от двух неизвестных функци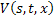й и :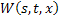

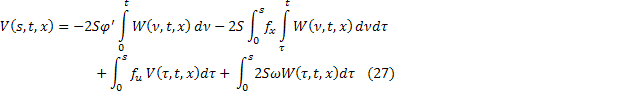
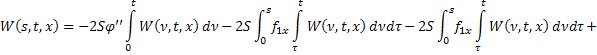
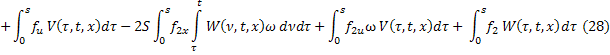
Обозначим через:

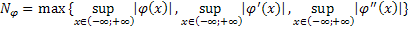
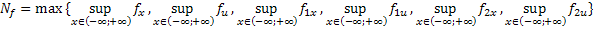
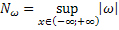
Тогда из (27) и (28):

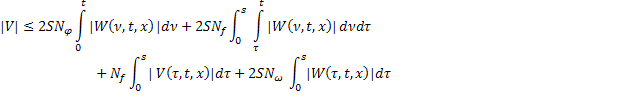
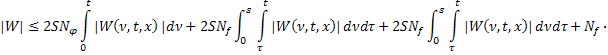
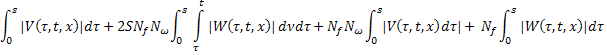
Или:

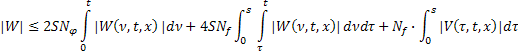
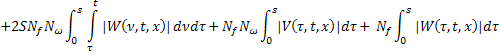
Меняя порядок интегрирования, будем иметь:

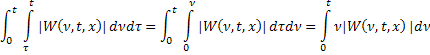
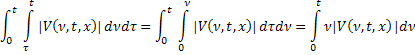
Обозначим через 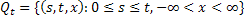, тогда для всех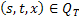

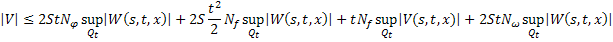
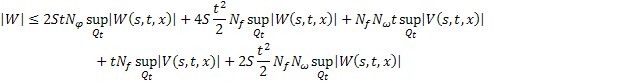
Обозначим через 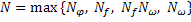, тогда:

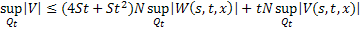
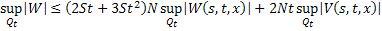
Складывая, получаем:

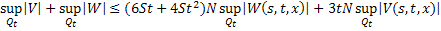
Обозначим через 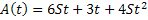. Очевидно, что для любого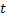

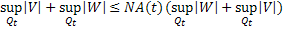
Обозначим через 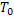значение t, при котором 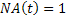. Тогда для любых t из промежутка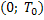 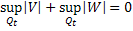, то есть 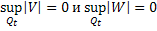, следовательно, что для любого 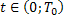выполняются тождества:

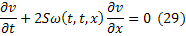
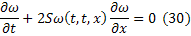
Подставим функции :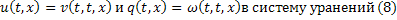

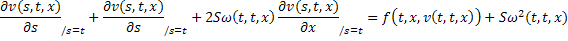
С учётом равенств (29) и (24), получим тождество:

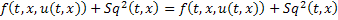
Аналогично для второго уравнения системы:

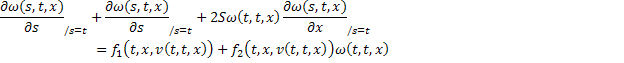
Учитывая (30) и (25), получим тождество:

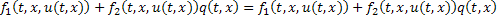
Проверим, что функции 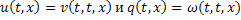удовлетворяют начальным условиям (2) и (9). Для этого подставим в (26) .

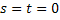В результате приходим к равенствам:

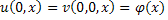
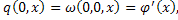
которые подтверждают, что решение системы (26) удовлетворяет начальным условиям (2), (9).

Итак, мы доказали, что решение задачи (8), (2), (9) даёт решение системы (26), и наоборот, непрерывно дифференцируемое решение системы (26) при ) 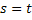будет решением задачи (8), (2), (9). То есть эквивалентность двух систем показана.

Доказательство существования решения задачи Коши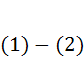

Осталось доказать существование ограниченного непрерывно дифференцируемого решения системы уравнений (26), тем самым будет доказано существование классического решения задачи Коши (1), (2).

Введём некоторые обозначения и определения.

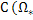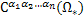Будем обозначать ) и – пространства функций определённых и непрерывных (соответственно со своими производными до порядка 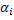по 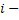му аргументу, 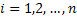) на некотором подмножестве 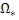евклидова пространства, .

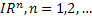Введём следующие обозначения:

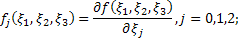
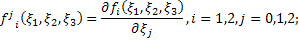
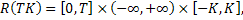
где 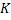– произвольно зафиксированное положительное число,

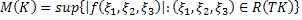
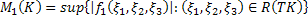
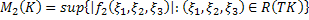
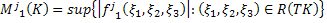
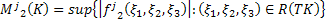
Также будем пользоваться ранее введённым обозначением:

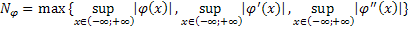
Для произвольной функци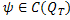и и 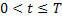мы положим:

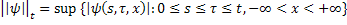
Лемма 1. Пусть 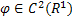, 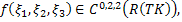причем 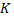и 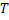подобраны таким образом, что выполняются неравенства

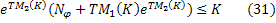
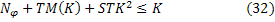
Пусть, далее 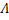– положительный корень уравнения

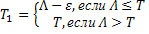
где 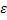- любое число из интервала (0, )

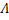и для любого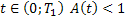

где

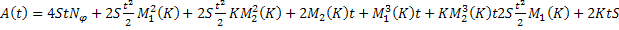
Тогда при 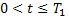система уравнений (26) имеет единственное решение.

Доказательство.

Будем доказывать существование решения системы уравнений (26) методом последовательных приближений. Положим:

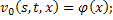
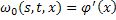
и будем строить последовательности функций

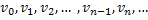
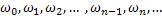
таким образом, что для всех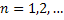

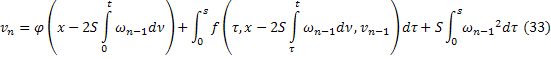
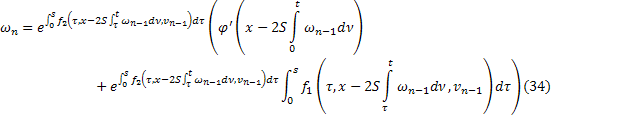
или

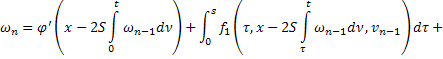
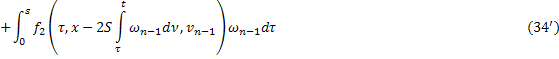
В силу (31), (32) из (34) и (33) все 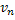, 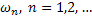будут ограничены:

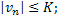
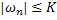
Будем доказывать, что последовательные приближения сходятся. Найдём разность:

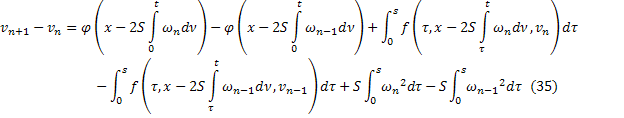
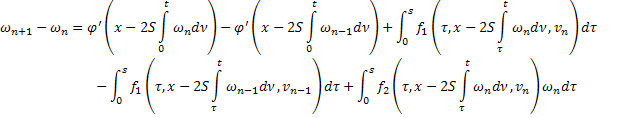
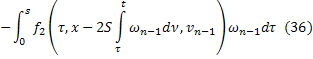
Заметим, что функция 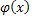имеет ограниченные производные на 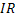, поскольку 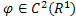, а

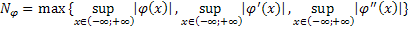
следовательно, 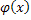удовлетворяет условию Липшица с константой :

| |=|

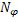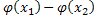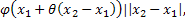
где 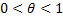, а значит

|

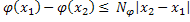
Аналогично для функции , , :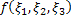

.

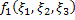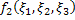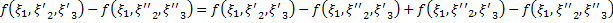
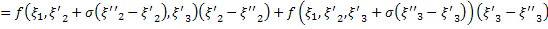Из этого равенства выводим, что

| |

| |

| |

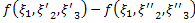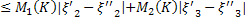
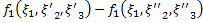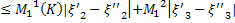
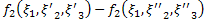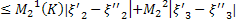
Из двух последних слагаемых (36):

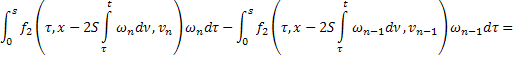
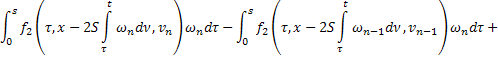
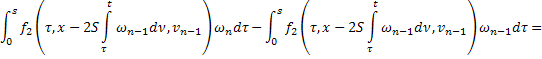
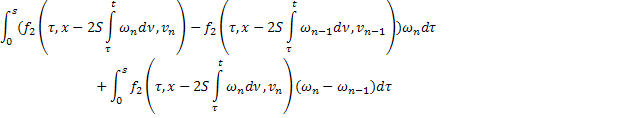
С учётом этих равенств получим из (36)

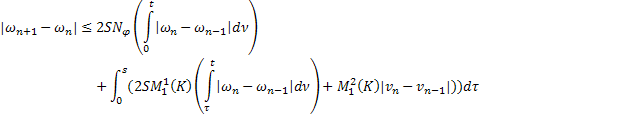
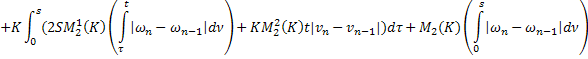
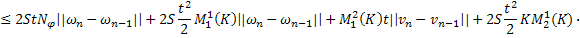
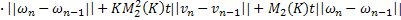
То есть:

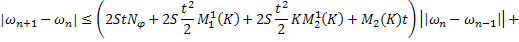
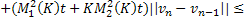
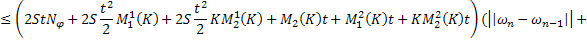
Аналогично из (35):

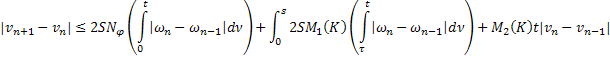
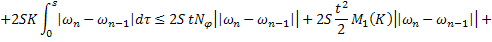
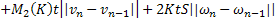
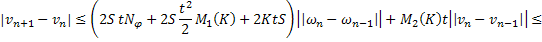
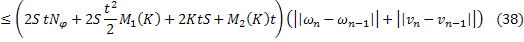
Сложим последние равенства (37) и (38):

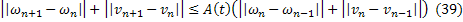
где

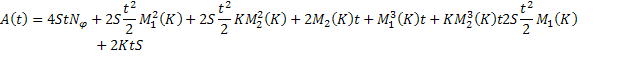
Рассмотрим вектор 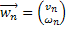. Будем доказывать, что последовательные приближения 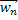сходятся по норме к вектору 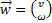. За норму вектора 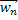положим сумму норм 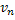и :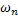

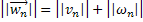
Тогда с учётом введённых обозначений равенство (39) перепишется в виде:

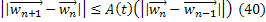
Пусть 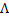- положительный корень уравнения 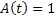. Тогда при любом 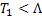ряд 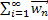сходится к вектору 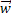. Именно, мы можем представить 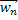в виде суммы:

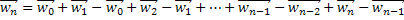
Ряд

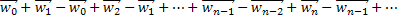
мажорируется сходящимся (так как 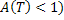рядом

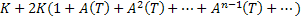
(здесь взято .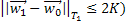

Это означает, что его частичная сумма сходится к вектору 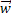по норме.

А это и означает, что ряды 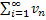и 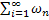также сходятся соответственно к функциям 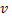и 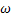по норме. Перейдя к пределу в равенствах (33) и (34), получим, что функци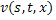и и 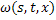, будут удовлетворять системе (26).

Единственность следует из того факта, что для разности двух возможных решений системы (26) будет выполняться неравенство вида

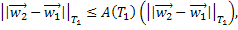
где .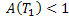

Лемма 2. При выполнении условий леммы 1 , .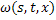

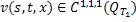Доказательство.

Согласно (25) функция

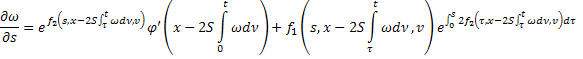
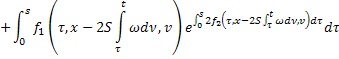
непрерывна и ограничена в 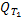(так как она получается из известных непрерывных и ограниченных функций с помощью конечного числа арифметических операций и композиций).

С учётом этого функция

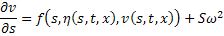
также непрерывна и ограничена в .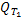

Чтобы доказать существование, непрерывность и ограниченность частных производных функци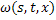й и 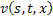продифференцируем по 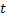соотношения, определяющие соответствующие последовательные приближения:

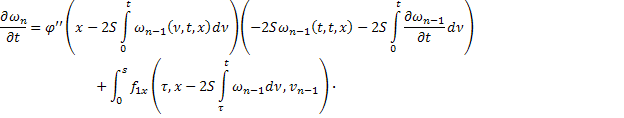
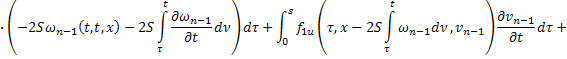
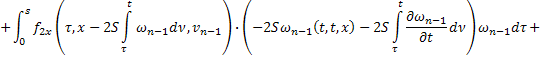
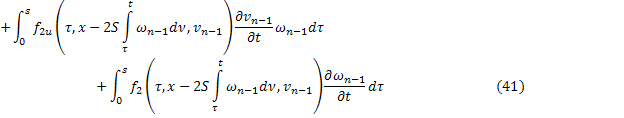
С учетом того, что

|

|

| |

| |

|

| |

|

| |

|

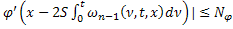
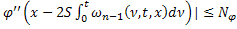
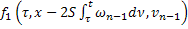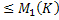
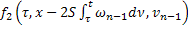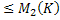
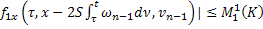
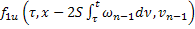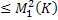
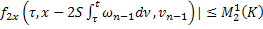
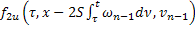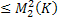
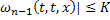
получаем:

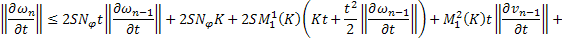
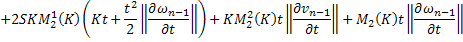
Приводя подобные, получаем:

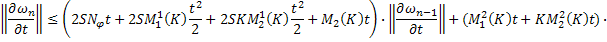
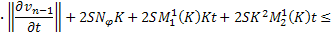
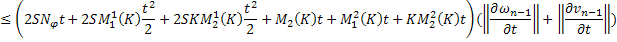
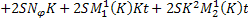
Аналогично для функции :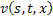

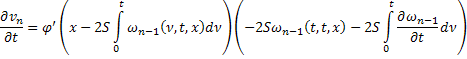
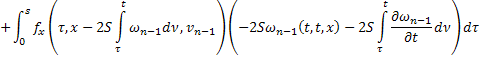
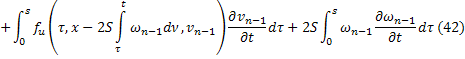
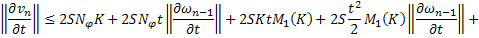
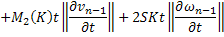
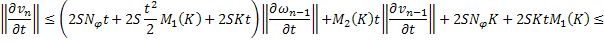
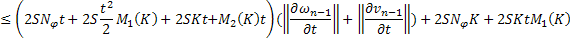
Складывая получившиеся равенства, получаем:

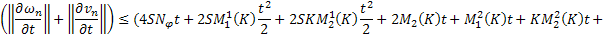
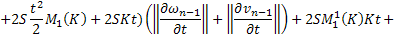
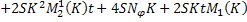
Вспоминая, что

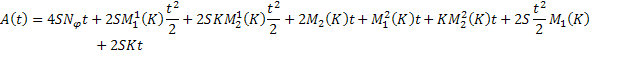
а также, что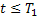

получаем:

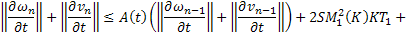
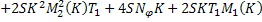
Обозначая за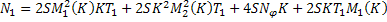

Снова введём в рассмотрение вектор 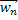. За его норму положим сумму норм 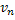и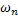

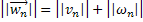
Тогда получаем:

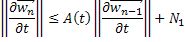
При 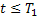имеем

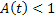
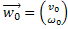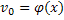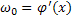Далее, так как , а , , то 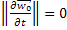, поэтому

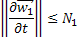
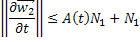
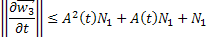
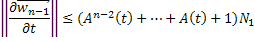
Пользуясь формулой бесконечно убывающей геометрической прогрессии, будем иметь:

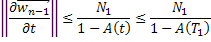
А это означает, что последовательность 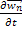ограничена по норме. Следовательно, ограничены по норме и последовательност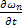и и .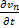

Чтобы несколько облегчить доказательство её сходимости, рассмотрим вначале линейные интегральные уравнения относительно неизвестных функци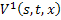й и 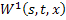и рассмотрим вектор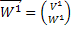

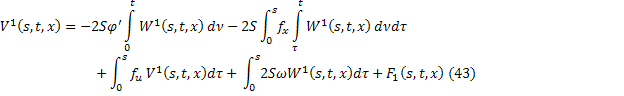
где

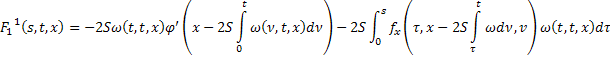
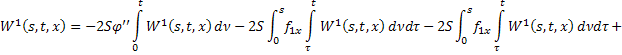
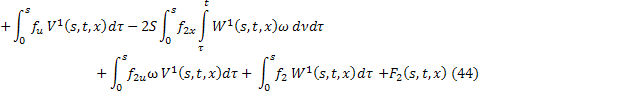
где

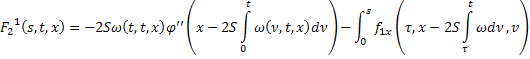
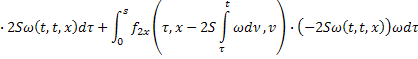
С помощью метода последовательных приближений доказывается, что уравнения (39) и (40) имеют решения, принадлежащие пространству .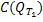

Из равенств (42) и (43):

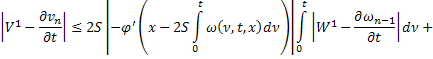
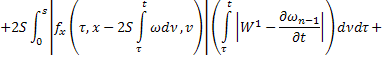
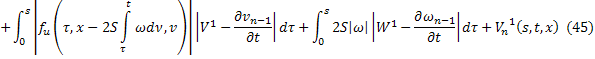
где

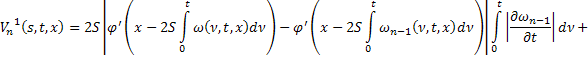
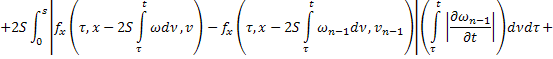
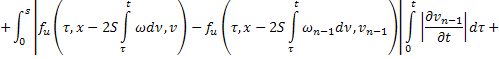
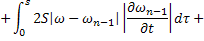
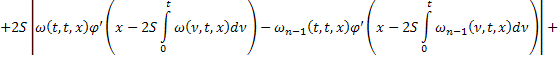
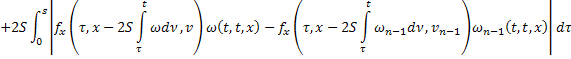
Аналогично из равенств (41) и (44):

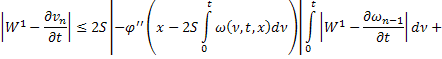
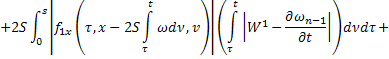
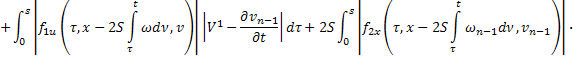
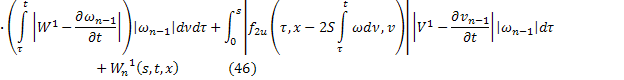
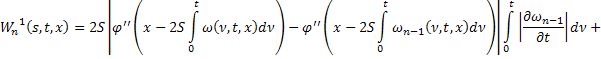
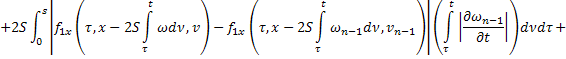
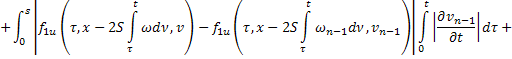
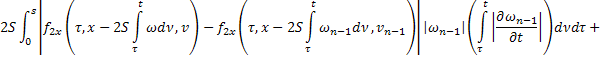
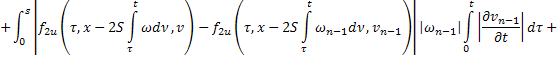
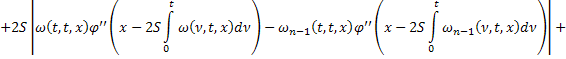
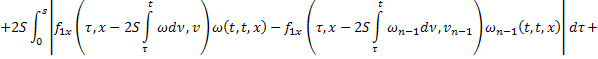
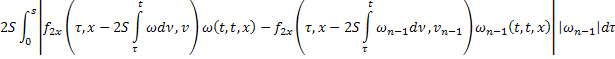
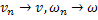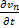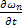В силу сходимости и ограниченности и при всех 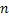для любого 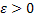можно определить такой номер 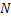, что для всех будет:

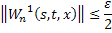
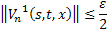
Переходя к норме в неравенствах (45) и (46), получаем

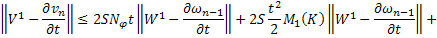
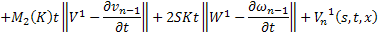
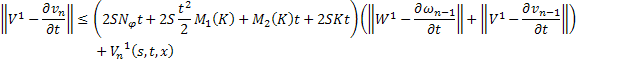
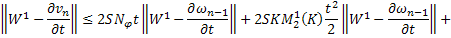
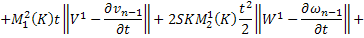
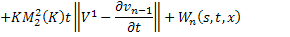
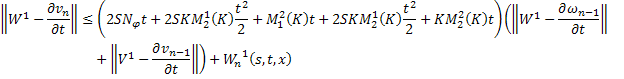
Складывая получившиеся неравенства и вспоминая, что

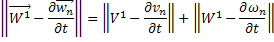
получаем, что для всех будет выполняться неравенство:

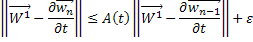
При 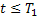имеем 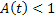, поэтому из предыдущего неравенства вытекает:

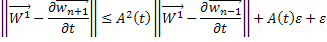
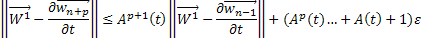
Таким образом, для любого 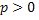будет выполняться неравенство:

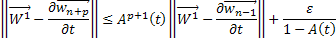
В силу того, что 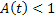для любого числа 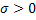можно определить такой номер 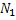, что для всех 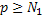будет

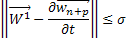
Этим самым мы доказали, что последовательность 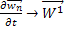при 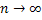, а значит и последовательност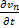и и 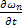сходятся соответственно к функциям 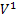и .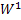

Точно также доказывается сходимость последовательносте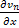й и 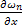к некоторым функциям 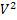и :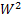

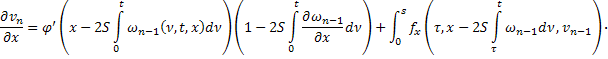
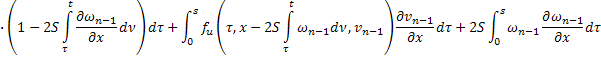
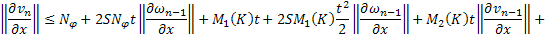
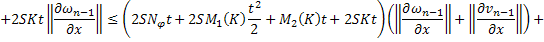
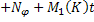
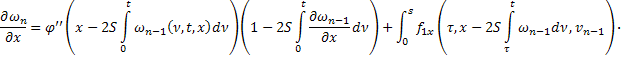
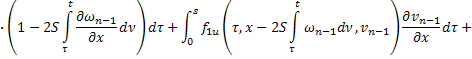
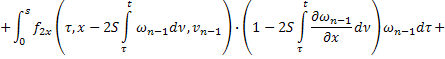
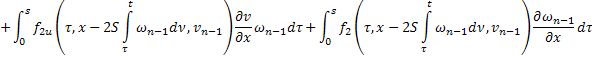
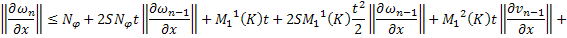
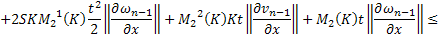
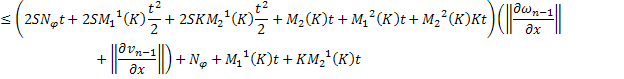
Складывая получившиеся неравенства, получаем:

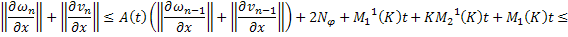
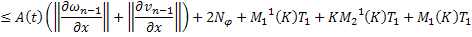
Обозначим

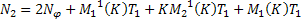
Тогда неравенство перепишется в виде:

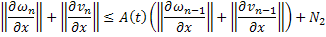
То есть

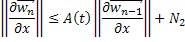
При 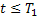имеем

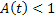
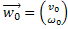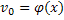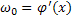Далее, так как , а , , то 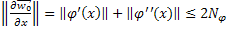, поэтому

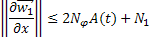
Обозначим

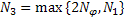
Тогда неравенство перепишется в виде:

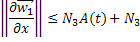
Увеличивая число 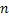, получаем:

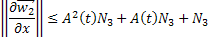
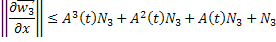
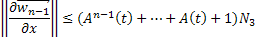
Пользуясь формулой бесконечно убывающей геометрической прогрессии, будем иметь:

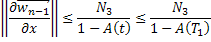
А это означает, что последовательность 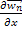ограничена по норме. Следовательно, ограничены по норме и последовательност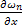и и .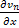

Чтобы несколько облегчить доказательство её сходимости, рассмотрим вначале линейное интегральное уравнение относительно неизвестных функци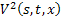й и 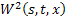и рассмотрим вектор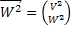

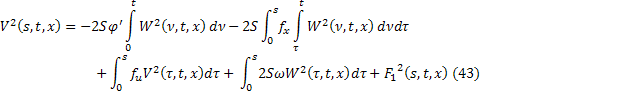
где

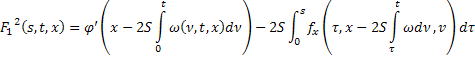
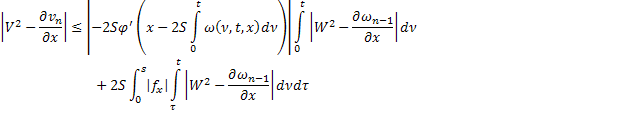
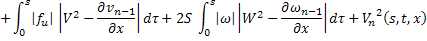
где

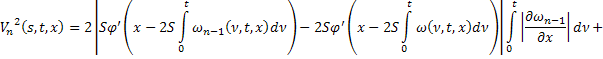
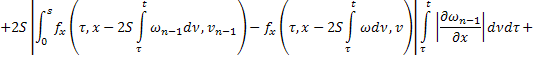
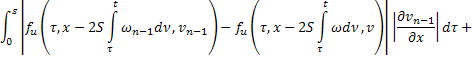
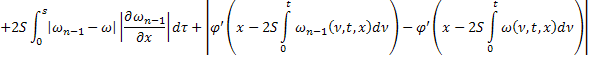
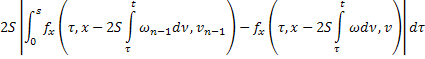
Аналогично для последовательности :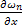

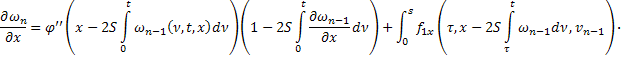
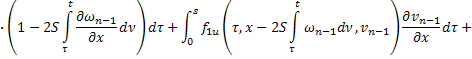
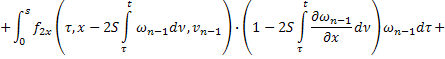
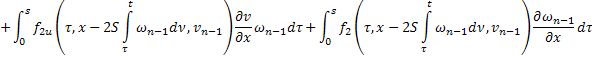
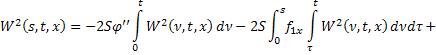
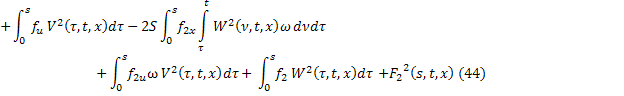
где

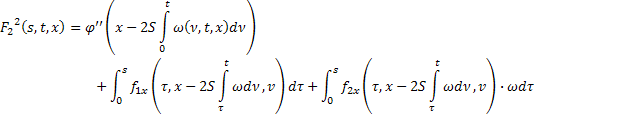
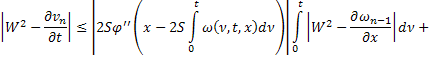
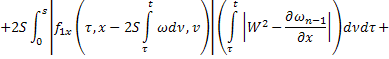
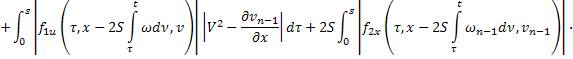
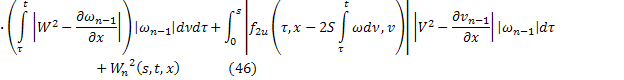
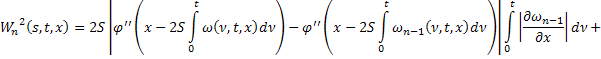
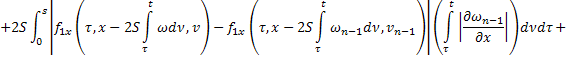
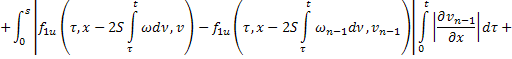
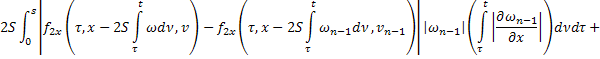
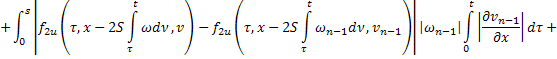
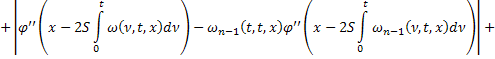
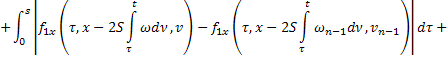
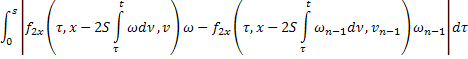
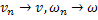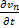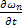В силу сходимости и ограниченности и при всех 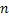для любого 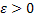можно определить такой номер 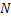, что для всех будет:

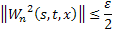
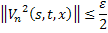
Переходя к норме в неравенствах (45) и (46), получаем

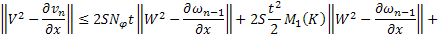
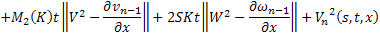
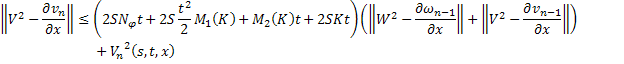
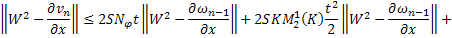
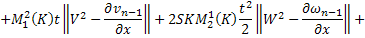
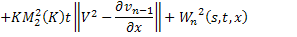
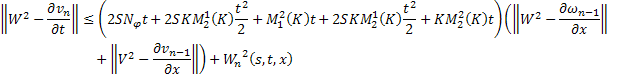
Складывая получившиеся неравенства и вспоминая, что

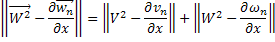
получаем, что для всех будет выполняться неравенство:

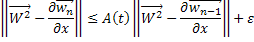
При 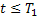имеем 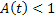, поэтому из предыдущего неравенства вытекает:

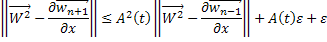
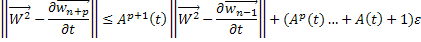
Таким образом, для любого 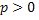будет выполняться неравенство:

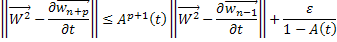
В силу того, что 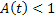для любого числа 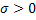можно определить такой номер 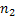, что для всех 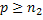будет

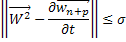
Этим самым мы доказали, что последовательность 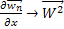при 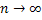, а значит и последовательност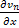и и 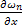сходятся соответственно к функциям 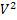и .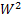

В результате для последовательносте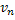й { } и { 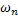} установлены следующие свойства:

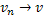
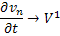
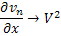
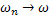
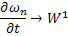
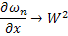
Имеем: последовательность 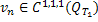, при любом 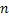сходится по норме этого пространства. В силу полноты и замкнутости пространства 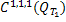имеем, что 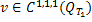, а значит, обладает частными производными по 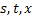, причём

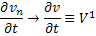
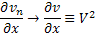
Аналогично 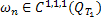, а значит

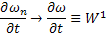
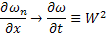
Таким образом, лемма 2 доказана.

На основе этих двух лемм и всего вышеизложенного, можно сформулировать общую теорему:

Теорема 1. Пусть на област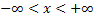и и 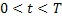задано нелинейное дифференциальное уравнение:

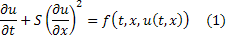
И пусть задано следующее начальное условие

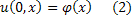
Если:

1) Функция 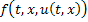непрерывна, ограничена, дважды непрерывно дифференцируема по переменным 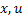и все вторые, а также смешанные производные удовлетворяют по этим переменным условию Липшица и ограничены при всех значениях аргументов.

2) Пусть функция 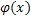дважды непрерывно дифференцируема на 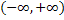, а её вторая производная ограничена и удовлетворяет условию Липшица.

Тогда существует такая константа 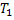, что при 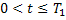задача (1) – (2) имеет единственное непрерывное и ограниченное вместе со своими первыми производными решение, которое совпадает при 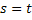с функцией 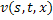, определяемой из системы интегральных уравнений (26).