A. Характеристики инвестиционного портфеля и основные допущения модели
Стратегии инвестирования на финансовых рынках
Семенихин А.И.
Введение и обзор
Инструменты инвестирования в современном мире – это, в основном, те или иные ценные бумаги. Чтобы показать объемы инвестирования приведем следующие цифры (данные 2006 года):
- ежедневный оборот на межбанковской валютной бирже Forex – 4 трлн. долл. (в год более 1200 трлн. долл.);
ежедневный объем мирового рынка ценных бумаг – около 300 млрд. долл. (в год более 90 трлн. долл.)
Для сравнения заметим, что мировой экспорт товаров за весь 2006 год составил 11,76 трлн. долл, а экспорт услуг - 2,71 трлн. долл.[1]
Применение вероятностного подхода к анализу движения цен фондового рынка ведет свою историю с диссертации француза Луи Башелье, опубликованной в 1900. Луи Башелье (Lui Bachelier, 1870-1946 г.г.) предложил рассматривать движение фондовых цен как «случайное блуждание». Приращения фондовых цен по его оценкам имели нормальное распределение.[2]
Работа Л. Башелье была недооценена современниками, практически забыта вплоть до своего повторного опубликования в 1964 году[3] в сборнике работ, посвященных вероятностным исследованиям фондового рынка. Сегодня Л. Башелье считается основателем финансовой математики.
В 60-70-х годах XX века идеи Л. Башелье получили развитие в работах П. Самуэльсона (Pall A. Samuelson), в моделях оценки опционов, предложенных Робертом Мертоном (Robert C. Merton) и Фишером Блэком (Fischer Black) вместе с Мироном Шоулзом (Myron Scholes).
Следующей революционной работой следует назвать статью Гарри Марковица (Harry Markowitz) «Выбор портфеля», опубликованную в 1952 году.[4] В последующие годы модель Г. Марковица получила развитие в работах Джеймса Тобина (James Tobin) и Уильяма Шарпа (William F. Sharpe).
Модель Марковица
A. Характеристики инвестиционного портфеля и основные допущения модели
Предполагается, что инвесторы измеряют доходность ценных бумаг в виде процента от первоначальных затрат[5]
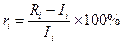 , где
, где
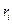 - доходность, норма прибыли;
- доходность, норма прибыли;
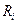 - прогноз будущей стоимости ценной бумаги в конце определенного периода плюс дивиденды, полученные за рассматриваемый период;
- прогноз будущей стоимости ценной бумаги в конце определенного периода плюс дивиденды, полученные за рассматриваемый период;
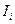 - размер первоначальной инвестиции.
- размер первоначальной инвестиции.
Если ожидаемая доходность ценной бумаги представляется случайной величиной, то средняя ожидаемая доходность 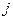 -ой ценной бумаги определяется как математическое ожидание от ее отдельных значений
-ой ценной бумаги определяется как математическое ожидание от ее отдельных значений
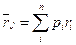
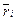 - средняя ожидаемая доходность;
- средняя ожидаемая доходность;
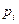 - вероятность
- вероятность 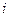 -ой доходности от
-ой доходности от 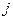 -ой ценной бумаги.
-ой ценной бумаги.
Одно из наиболее важных допущений заключается в том, что разброс доходности ценных бумаг относительно их ожидаемых значений является для инвестора мерой риска, связанной с каждой акцией. Этот разброс измеряется либо среднеквадратическим отклонением 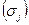 , либо дисперсией
, либо дисперсией 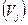 относительно ожидаемого доходности
относительно ожидаемого доходности 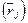 . Вообще, допущение, что доходность и мера риска дают полное описание любой ценной бумаги или портфеля является для модели Марковица основным, но небесспорным. [6]
. Вообще, допущение, что доходность и мера риска дают полное описание любой ценной бумаги или портфеля является для модели Марковица основным, но небесспорным. [6]
Обратим внимание, что в финансовой математике принято дисперсию называть волатильностью и обозначать 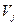 .
.
Каким образом могут быть определены ожидаемая доходность и дисперсия по каждой ценной бумаге? Марковиц Г. в своей статье «Выбор портфеля» специально оговорил, что задачи определения параметров отдельных ценных бумаг он не рассматривает и исследует лишь формирование параметров портфеля при известных параметрах отдельных бумаг.
Распределение вероятностей может отражать субъективные оценки вероятностей различных исходов. Другие авторы полагают, что на будущий период могут переноситься средние фактические доходы и отклонения прошлых периодов[7]
Предполагается также, что распределение вероятностей ожидаемой доходности относится к нормальному типу. В этом случае средняя доходность – математическое ожидание - является наиболее вероятной в будущем периоде и достаточно знать среднюю величину ожидаемой доходности и ее дисперсию. Возможно использование полудисперсии, учитывая, что инвесторы в большей степени обеспокоены падением доходности ниже определенного уровня. Правда, при нормальном распределении значений доходности отклонения от среднего в ту или иную сторону равны друг другу и результаты расчетов не меняются. В некоторых случаях распределение доходности может быть приведено к нормальному типу тем или иным способом [8]
