Операционные усилители (ОУ)
ОУ – это интегральная микросхема представляющая собой многокаскадный усилитель постоянного тока с дифференциальным входным каскадом, большим коэффициентом усиления и глубокой ООС.
Термин «ОУ» возник от первоначального назначения этих усилителей – выполнение математических операций. На основе ОУ можно выполнить более 200 преобразований над сигналами.
Современные ОУ состоят, как правило, из 3-х каскадов, например:
1 каскад – дифференциальный каскад с большим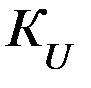 
и несимметричным выходом.
2 каскад – усилитель, собранный по схеме ОЭ.
3каскад – двухтактный бестрансформаторный УМ на комплементарной паре.
Обозначение ОУ:
∞
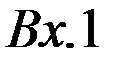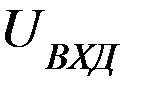
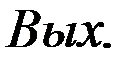
+Еп
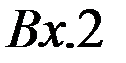-Еп
основное поле дополнительное поле
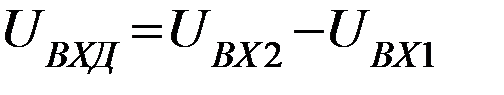
Равносторонний треугольник на основном поле указывает направление передачи сигнала. Знак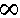 
означает высокий 
.
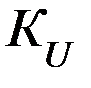Вход 1 называется инвертирующим (сигнал с него передается на выход
ОУ с изменением фазы на 180 градусов).
Вход 2 – не инвертирующий (сигнал с него передаётся на выход ОУ без
изменения фазы).
На дополнительном поле указываются выводы питания, корпуса, балансировки нуля, коррекции.
Параметры ОУ
1.Коэффициент усиления дифференциального сигнала (часто этот коэффициент называется просто «коэффициент усиления»):
( 
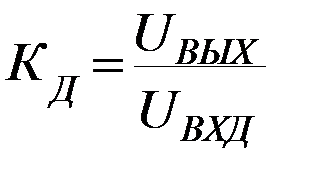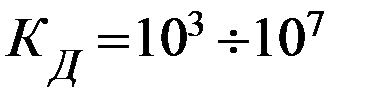,т.е. очень велик).
2. Коэффициент ослабления синфазного сигнала: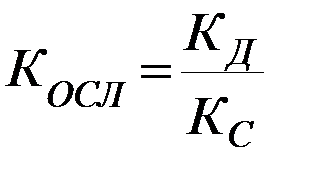 
, где
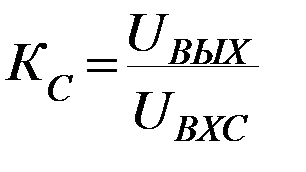- коэффициент усиления синфазного сигнала
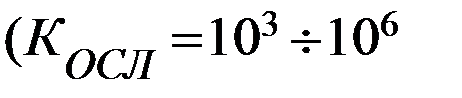,т.е. велик)
3. Входное сопротивление ОУ. Это сопротивление большое (до десятков÷сотен МОм). Оно обеспечивает поступление на вход ОУ полезного сигнала (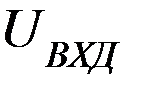 
) практически без потерь – достоинство.
4. Выходное сопротивление ОУ определяется схемой оконечного каскада. Оно мало (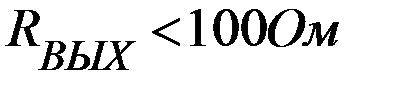 
), поэтому всё выходное напряжение передаётся в нагрузку практически без потерь – достоинство.
5. Полоса пропускания ПП = (0 ÷ десятки) МГц, т.е. велика.
Вывод: по своим параметрам ОУ приближается к идеальному.
Т.к. ОУ имеет большой коэффициент усиления, то даже малое постоянное дифференциальное входное напряжение, вызванное асимметрией схемы (например, из-за разброса параметров) приведёт к появлению на выходе недопустимо большого постоянного напряжения, что вызовет перегрузку усилителя.
Чтобы этого избежать, в ОУ применяется глубокая внешняя ООС.
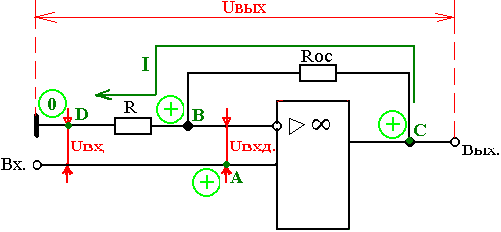
Инвертирующий ОУ
Название говорит о том, что входной сигнал подаётся на инвертирующий вход, не инвертирующий вход заземлён. Напряжение обратной связи (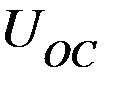 
) также должно подаваться на инвертирующий вход (иначе ОС будет положительной, что недопустимо).
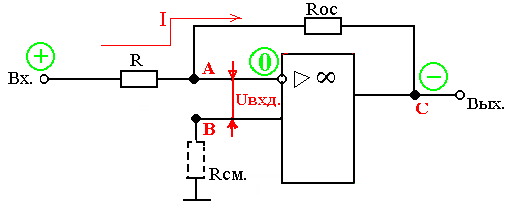
Выводы питания и корпуса опущены.
Считаем, что ОУ близок к идеальному: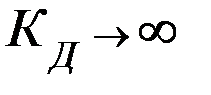 
; 
; 
.
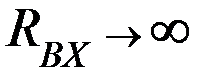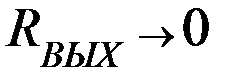Пусть на входе положительный потенциал, т.е.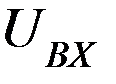 
> 0.
Рассмотрим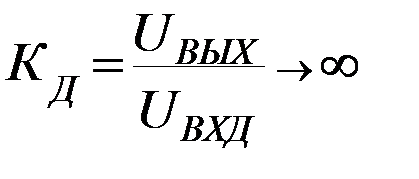 
. Дробь стремится к бесконечности, если числитель стремится к бесконечности или знаменатель стремится к 0.
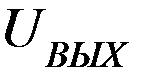к бесконечности стремиться не может, т.к. ограничивается напряжением источника питания, следовательно,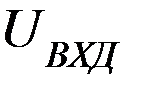 
0.
Это означает, что потенциал точки А совпадает с потенциалом точки В и будет равен 0, т.к.точка В имеет нулевой потенциал (соединена с корпусом): (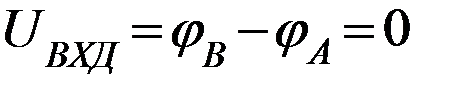 
, т.е. 
).
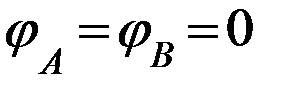Таким образом, через резистор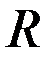 
ток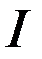 
течёт слева направо (от бо́льшего потенциала к меньшему). Т.к. 
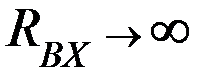, то этот ток будет течь через резистор 
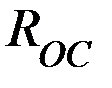, минуя усилитель. Поскольку потенциал 
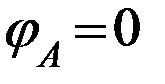, а ток течет от большего потенциала к меньшему, то 
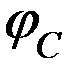< 0.
Таким образом, произошла инверсия входного сигнала (на входе положительный потенциал, на выходе – отрицательный), отсюда и название ОУ – инвертирующий.
Во входной и выходной цепях протекает один и тот же ток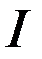 
, поэтому можно записать: 
(*)
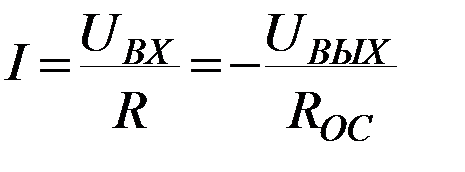2-й закон Кирхгофа: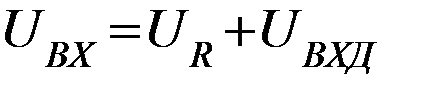 
, т.к. 
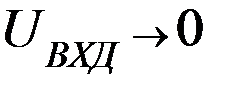, то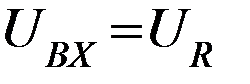 
,
т.е. все входное напряжение падает на .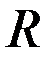
Т.к.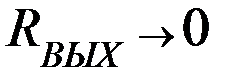 
, то все выходное напряжение падает на .
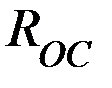Минус в выражении (*) стоит потому, что выходное напряжение противофазно входному.
Из выражения (*) находим: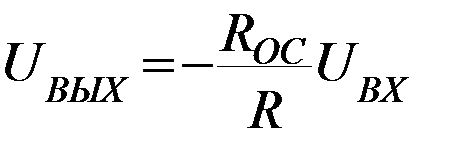 
.
Учитывая, что: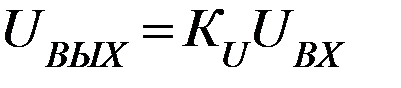 
, получаем 
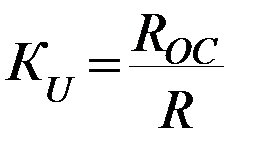, где 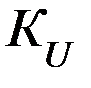- коэффициент усиления инвертирующего ОУ.
Резистор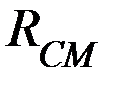 
служит для компенсации сдвига нуля на выходе ОУ (для компенсации дрейфа), вызванного токами смещения.
Не инвертирующий OУ
Входной сигнал подаётся на не инвертирующий вход ОУ, напряжение ОС через делитель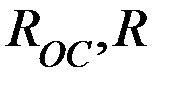 
- на инвертирующий вход (иначе ОС будет положительной, что недопустимо).
Считаем, что ОУ близок к идеальному: (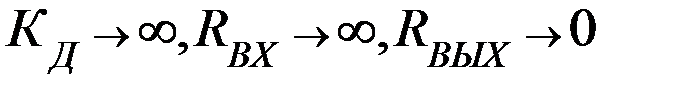 
).
Пусть на входе положительный потенциал, т.е.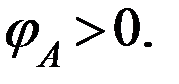 
Коэффициент усиления будет стремиться к бесконечности при условии, что 
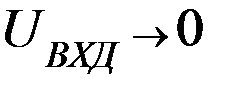, т.к. выходное напряжение ограничено напряжением источника питания и стремиться к бесконечности не может ( 
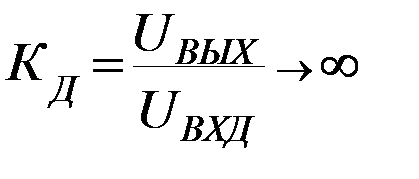). Это означает, что потенциал точки А совпадает с потенциалом точки В: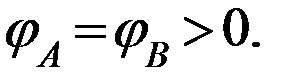 
Т.к. потенциал точки Д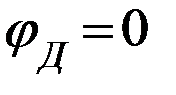 
(корпус), а ток течёт от большего потенциала к меньшему, то через резистор 
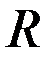ток 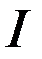будет протекать справа налево. Естественно предположить, что этот ток поступает на резистор 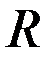с выхода через резистор 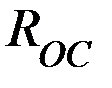, минуя ОУ (т.к. 
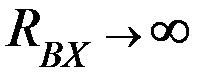). Отсюда делаем вывод: 
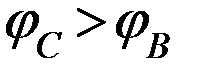, т.е. 
.
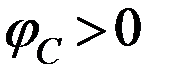Таким образом, инверсии не произошло: выходное напряжение совпадает по фазе с входным, отсюда и название ОУ – не инвертирующий.
С учётом того, что входное и выходное напряжения определяются относительно корпуса и ток во входной и выходной цепях протекает один и тот же, можно записать: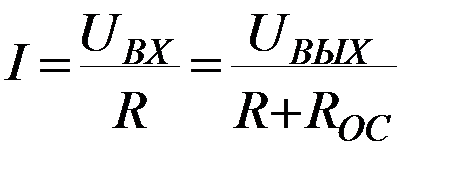 
(**)
Все входное напряжение падает на 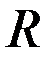, т.к. 
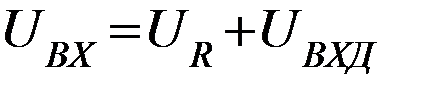, а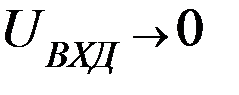 
.
Все выходное напряжение падает на (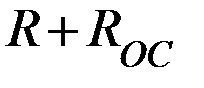 
), т.к. 
.
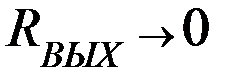Из выражения (**) находим: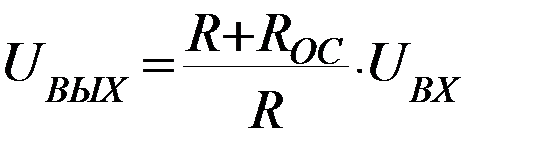 
.
Учитывая, что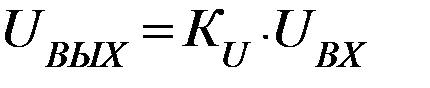 
, получаем 
,
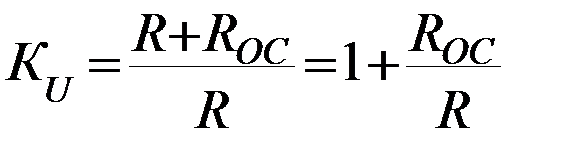где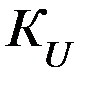 
- коэффициент усиления не инвертирующего ОУ.
Интегратор
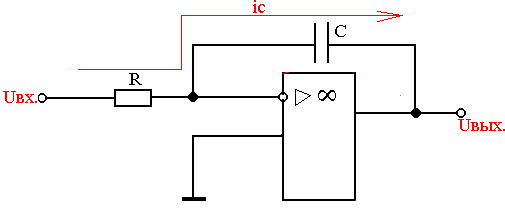
Интегратор выполнен на основе инвертирующего усилителя. Конденсатор 
включен в цепь ОС и заряжается током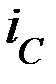 
.
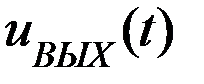
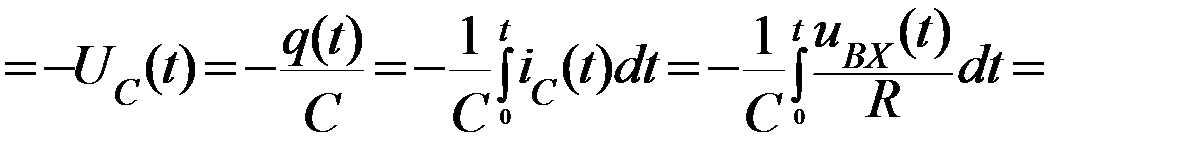
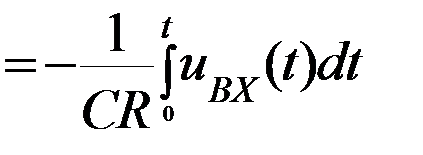
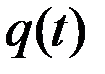
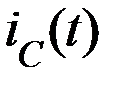
Таким образом, выходное напряжение связано с входным через интеграл, отсюда и название – «интегратор».
Рассмотрим частные случаи:
1) Если 
, то выходное напряжение интегратора будет линейным: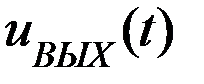 
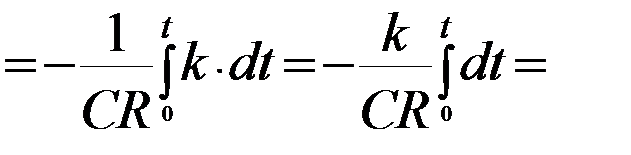
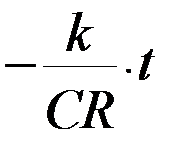
uВХ
o t
uВЫХ
o t
3) Если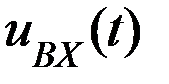 
– последовательность прямоугольных импульсов, то выходное напряжение будет пилообразным.
uВХ
o t
uВЫХ
o t
Дифференциатор
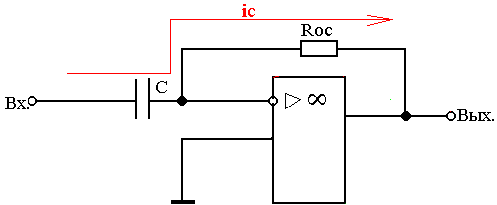
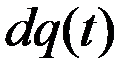
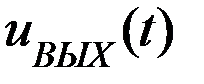
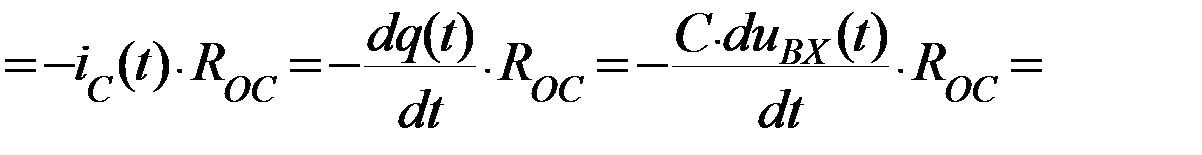
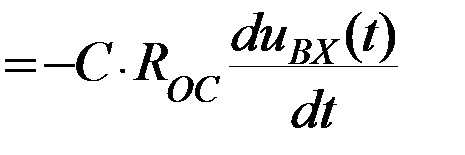
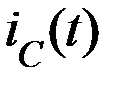
Таким образом, выходное напряжение связано с входным через дифференциал, отсюда и название – «дифференциатор».
Рассмотрим частные случаи:
1) Если на входе будет линейное напряжение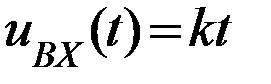 
, то на выходе будет постоянное напряжение:
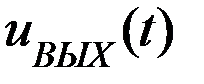
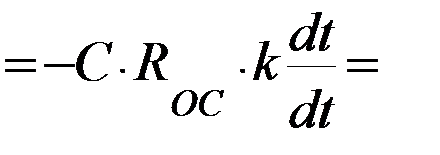
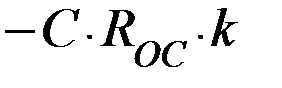
UВХ
t
UВЫХ
o t
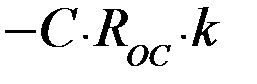
2) Пусть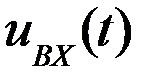 
– последовательность прямоугольных импульсов.
Дифференциал ступенчатой функции представляет собой импульс бесконечно малой длительности и бесконечно большой высоты. Приближением к такой функции является экспонента.
uВХ
o t
uВЫХ
o t
Литература
1 Аксенов А.И., Нефедов А.В. Отечественные полупроводниковые приборы.
Справочное пособие.- М.: Салон-пресс, 2012. – 525с.
2 Берикашвили В.Ш., Черепанов А.К. Электронная техника. – М.: Академия, 2012. – 336с.
3 Гальперин М.В. Электронная техника. – М.:ИД «ФОРУМ» - Инфра-М, 2012.- 351с.
4 Полищук В.И. Задачник по электронике. М.: Академия, 2011. – 156с.
5 Сиренький И.В., Рябинин В.В., Голощапов С.Н. Электронная техника. Из-во Питер, 2011. – 416с.
6 В.И.Галкин, Е.В.Пелевин Промышленная электроника и микроэлектроника,
М.: Высшая школа, 2013-350с.
7 studentbank.ru/view.php?id=42336
8 review3d.ru/elektronika-kurs-lekci
9 fanknig.org/book.php?id=24206316
10 padabum.com › Электроника