Программы анализа качества процессов управления

Современные инструментальные средства анализа и синтеза систем управления представлены множеством различных специализированных программных пакетов и комплексов, которые позволяют в диалоговом режиме выполнять операции над матрицами и полиномами, вычислять временные и частотные характеристики, строить корневые годографы, анализировать чувствительность и устойчивость, проверять управляемость и наблюдаемость системы, находить ее полюса и нули, сравнивать переходные процессы в системе по интегральным критериям и находить лучший, определять параметры и характеристики стохастических сигналов на входе и на выходе системы, составлять и преобразовывать математические модели исследуемой системы.

Эти программные средства обладают развитым сервисом, что позволяет строить и сравнивать графики нескольких процессов, изображать взаимные зависимости, фазовые кривые и портреты, строить характеристики и диаграммы, изображать и преобразовывать структурные модели системы, при этом графические построения могут быть выполнены в двух- и трехмерном представлении ,

Известны фирменные и университетские программные пакеты анализа и синтеза систем управления: LSАР - США (Ливерморская национальная лаборатория) ТUТSIМ - США (Станфордский университет); СLADP - Великобритания (Кембридж); КЕDDС - Германия (Рурский университет); МАТRIХ - фирмы Integrated Systems Inc .; SIMULINK в среде МАТLАВ известной фирмы Маth Works Inc .; МАRS - Украина (Институт кибернетики). Известны разработки Академии авиационного и космического приборостроения, Санкт-Петербург; МОСКОВСКОГО ИНЖЕНЕРНО-физического института; Московского государственного технического университета; Института проблем управления РАН, Москва.

Программные комплексы ТUТSIМ, МАТRIХ, SIMULINK позволяют исследовать модели любых динамических систем, которые испытывают любые внешние воздействия. Комплексы обеспечивают команды изменения структуры модели, ее параметров, выходных блоков и диапазонов рассчитываемых данных; команды одиночного и многократного запуска, останова и продолжения процесса моделирования с выводом графиков и числовых данных на экран, принтер или в файл; команды графического сервиса, позволяющие изображать оси, сетку, маркировку, комментарии к графикам, строить фазовые кривые или взаимозависимости и прочее. Комплексы располагают различными функциональными блоками для моделирования любых непрерывных и дискретных, линейных и нелинейных динамических систем, испытывающих детерминированные и стохастические воздействия.

5. Анализ инвариантности САУ.

В теория автоматического управления (ТАУ)под инвариантностью САУ понимают независимость управляемой (выходной) величины САУ y(t) от одного или нескольких возмущений z1 – z3 и независимость рассогласования (t) следящей системы от управляющего (задающего) воздействия g(t).

В простейшем случае инвариантности САУ достигают посредством принципа управления по возмущению. При этом управляющее устройство, которое называют компенсатором, под влиянием возмущения z(t) воздействует на ОУ.

В результате этого непосредственное (естественное) влияние возмущения z(t) на управляемую величину y(t) уравновешивается. Единственная цель управления при этом состоит в устранении влияния одного, заранее выбранного возмущения. Компенсируют только одно возмущение, однако возможна полная компенсация. Компенсатор для этого должен иметь измерительное устройство (ИУ) для измерения возмущения z(t) и исполнительный механизм (ИМ) для создания необходимого воздействия yр(t) на ОУ. Таким образом, компенсация возмущения достигается специальной структурой САУ (структурная компенсация возмущения). Кроме того, система управления должна удовлетворять условию инвариантности. Структурный признак реализуемости условия инвариантности сформулирован Б.Н.Петровым в форме признака двухканальности: в динамической системе должно быть по крайней мере два канала воздействия возмущения на координату (управляемую величину), инвариантность которой от этого возмущения должна быть обеспечена. Только в этом случае воздействие возмущения по одному каналу может быть компенсировано противоположным по знаку воздействием этого же возмущения по другому каналу (пунктирная линия 2).

Принцип двухканальности – это необходимый, но недостаточный критерий реализуемости условия инвариантности. Достаточным критерием реализуемости условия инвариантности считают возможность физической осуществимости необходимых для этого реальных элементов САУ.

Трудности реализации условия инвариантности обусловили целесообразность создания САУ и с приближенным его удовлетворением. Поэтому в зависимости от степени реализации условия инвариантности и получаемых результатов различают следующие виды инвариантности:

1) абсолютную;

2) полную с точностью до переходной составляющей;

3) частичную до l-й производной включительно;

4) частичную с точностью до малой величины.

Под абсолютной инвариантностью регулируемой величины понимают совершенную независимость ее от возмущения, момента приложения возмущения к САУ и его последующего изменения.

Если от возмущения не зависит лишь установившееся значение регулируемой величины, то говорят о полной инвариантности. В этом случае начальные значения возмущения и его производных обусловливают переходную составляющую регулируемой величины.

Под частичной инвариантностью понимают независимость регулируемой величины в установившемся режиме лишь от абсолютного значения возмущения и его младших производных до l-й включительно. Причина названной "частичности" заключается в физической нереализуемости элементов САУ, необходимых для обеспечения условия инвариантности.

Вследствие неизбежных неточностей возможно только приближение к абсолютной, полной или частичной инвариантности. Влияние возмущения на регулируемую величину оказывается существенно уменьшенным, но проявляет себя в переходных и установившихся режимах. В том случае достигают инвариантности с точностью до малой величины.

Аналогично классифицируют инвариантность рассогласования от задающего воздействия в комбинированных следящих системах. Рассмотрим следующую систему, на вход которой поступает задающее воздействие х(t), а на вход объекта управления - возмущающее воздействие v(t) (рис.11).

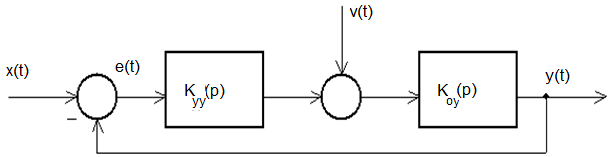
Рис.11. Структурная схема САУ.

Основное назначение системы в том, чтобы выходная величина y(t) c течением времени изменялась в соответствии с изменением задающего воздействия x(t) и мало зависела от изменения возмущающего воздействия v(t).

Уравнение относительно изображения выходной величины y(p) состоит из двух частей. Каждая из этих частей представляет собой произведение соответствующей передаточной функции на свое воздействие. В рассматриваемом случае

y(p) = K_yx(p)x(p) + K_yv(p)v(p) (1)

где 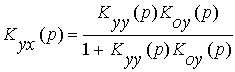- передаточная функция замкнутой системы

и 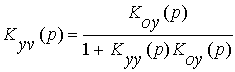- передаточная функция по возмущающему воздействию. Поскольку изображение ошибки e(p) равно

e(p)=x(p)-y(p) (2)

то, подставляя y(p) из (1) в (7.narod.ru/grom/ch_23.htm"2), получим уравнение относительно изображения ошибки

e(p) = x(p) - K_yx(p) x(p) - K_yv(p) v(p) = (1-K_yx(p)) x(p) - K_yv(p) v(p).

Передаточная функция ошибки по задающему воздействию равна:

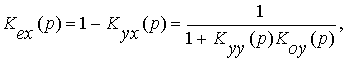
а передаточная функция ошибки по возмущающему воздействию отличается лишь знаком от К_yx(p).

Степень влияния изображений задающего и возмущающего воздействий на изображение выходной величины y(p) или изображение ошибки e(p) определяется соответствующими передаточными функциями. Для уменьшения влияния возмущающего воздействия на выходную величину и ошибку следует уменьшать коэффициент преобразования передаточной функции K_yx(p).Для того, чтобы выходная величина лучше воспроизводила задающее воздействие, или, что эквивалентно, для того, чтобы ошибка была близка к нулю, следует K_yx(p) приближать к единице.

Поскольку управляемый объект задан, то его передаточную функцию K_yx(p) невозможно изменять по своему усмотрению. Мы можем изменять лишь параметры элементов управляющего устройства. При увеличении K_yy(p) передаточная функция K_ev(p) будет уменьшаться, стремясь к нулю, а передаточная функция K_yx(p) будет возрастать, стремясь к 1. Следовательно, в пределе при бесконечно большом коэффициенте преобразования управляющего устройства

1-K _yx(p)=0, K_ev(p) = 0 .

Эти условия означают, что передаточные функции ошибки по задающему и возмущающему воздействиям равны нулю при всех значениях p, т.е. тождественно равны нулю. При выполнении этих условий получаем y(p) = x(p) и e(p) = 0, что соответствует идеальной системе с нулевой ошибкой. Выходная величина системы перестает зависеть от возмущающего воздействия и начинает точно воспроизводить задающее воздействие.

Таким образом, условием инвариантности системы является тождественное равенство нулю передаточных функций ошибки по задающему и возмущающему воздействиям. Условия инвариантности состоят из условия компенсации -тождественного обращения в нуль передаточной функции ошибки по возмущающему воздействию K_ev(p) = 0 и условия воспроизведения -тождественного обращения в нуль передаточной функции ошибки по задающему воздействию.

Если в автоматической системе выполняется какое-либо одно из этих условий, то систему можно назвать частично инвариантной.

Инвариантные и частично инвариантные системы представляют собой идеальные системы. Такие системы как правило физически нереализуемы. Однако знакомство с такими идеальными системами весьма важно, так как они определяют тот предел, к которому следует приближаться при желании синтезировать высококачественные системы с учетом реальных возможностей и ограничений.