Метод корреляционного анализа

Математические модели процессов на основе методов корреляционного и регрессионного анализа

1. ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРОЦЕССОВ

Методы построения математических моделей:

1. Использование физических закономерностей протекания процессов.

2. Экспертно-модифицированные закономерности на основе эмпирических оценок.

3. Методы группового учета аргументов, ориентированные на использование опытных данных по процессу и ЭВМ.

Полученные различными методами математические модели предназначены для оптимизации процессов. Оптимизация осуществляется методами вариационного исчисления и динамического программирования (для управления объектами со сложными динамическими характеристиками), линейного программирования и различных градиентов (для технологических процессов с большими постоянными времени).

2. ФОРМУЛИРОВКА ЗАДАЧИ И МЕТОД ЕЕ РЕШЕНИЯ

В зависимости от выбранной модели объекта управления системы управления подразделяются на три класса:

Технологические

p(t) = Mp_т(t) + p_т(t);

организационные

p(t) = Mp_ор(t) + p_ор(t);

комплексные

p(t) = Mp_op(t) + Mp_т(t) + p_op(t) + p_т(t),

где p_op(t), p_т(t) – компоненты характеристики, значения которых определяются организационными и технологическими процессами; t – некоторая независимая переменная; Mp_op(t), Mp_т(t) – компоненты математического ожидания значения данного параметра, определяемые организационными и технологическими процессами.

При создании системы управления любого класса предварительно необходимо найти хотя бы одну из функций Mp_т(t) или Mp_ор(t). Для этого использую два способа: априорный, когда вид зависимости Mp_т(t) или Mp_ор(t) выбирают исходя из некоторых теоретических предпосылок об исследуемом объекте; апостериорный, когда Mp_т(t) или Mp_ор(t) определяют экспериментально.

Для технологических процессов, не имеющих точного детерминированного математического описания, задача построения математической модели технологического процесса в основном сводится к нахождению функции Mp_т(t) и реже p_т(t). В этом случае, при решении такой задачи, используются методы, основанные на корреляционном и регрессионном анализе.

Метод корреляционного анализа

Метод корреляционного анализа определяет статистическую взаимосвязь влияния технологических или организационных факторов на характеристики выпускаемой продукции, посредством нахождения эмпирических коэффициентов корреляции и корреляционных отношений.

Экспериментальные исследования зависимостей процессов и параметров изделий дают определенные разбросы экспериментальных данных, характеризующих эти связи. При их построении получают корреляционные поля, отражающие статистический характер исследуемых зависимостей (рис. 1). Предварительно разбив ось абсцисс или ординат на интервалы и сгруппировав экспериментальные данные по интервалам, можно получить корреляционные зависимости (рис. 2).

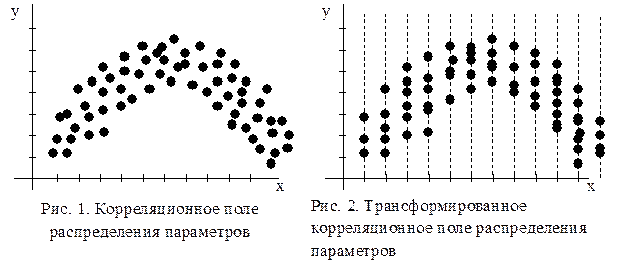
При исследовании корреляционных отношений предварительно необходимо установить характер изучаемых распределений, так как при расчетах корреляционных связей используются только два параметра распределения: среднее и дисперсия, которые полностью определяют только нормальный и логарифмический законы распределения.

Значение коэффициента линейной корреляции r лежит в пределах –1 £ r £ 1. Если r = 0, тогда линейной корреляционной связи между х и у нет; если çrç= 1, тогда между х и у имеется жесткая функциональная зависимость.

Коэффициент линейной корреляции r используют только для определения статистической взаимосвязи линейно зависимых переменных.

Коэффициент линейной корреляции для двух переменных х и у:

; ;

; ; ,

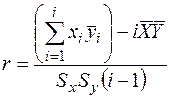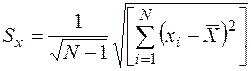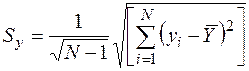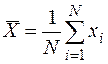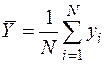где S_x, S_y – несмещенные и состоятельные оценки среднеквадратических отклонений s_х и s_у; 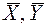– несмещенные и состоятельные оценки средних значений х и у; N – число результатов измерений, 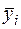– выборочное среднее на i-м уровне входного фактора х.

Для установления факта статистической зависимости при нелинейной взаимосвязи переменных возможно использование коэффициента линейной корреляции. Однако необходимо проверить следующее соотношение:

r ³ r_кр,

где

;

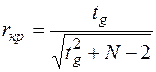t_g – критерий Стьюдента для g-процентной доверительной вероятности [4, 5], а также для числа степеней свободы i(u – 1), где i – число уровней входного фактора; u – число повторений эксперимента на уровне фактора.

Для оценки статистической взаимосвязи нелинейно-зависимых переменных используют корреляционное отношение Пирсона h_х/у (для зависимости х от у) и h_у/х (для зависимости у от х):

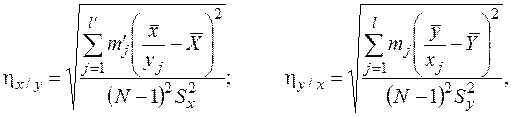
где l, l¢ – число интервалов, на которые разбиваются ординаты х и у; m_j, m_j¢ – число наблюдений (x_ij, y_ij), абсциссы которых попали в j-й интервал; 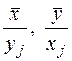– условные средние:

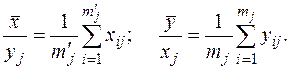
Для корреляционного отношения всегда справедливо неравенство 0 £ h £ 1. При h = 1 между переменными х и у имеется детерминированная функциональная зависимость; при h = 0 зависимости между переменными нет, при этом из равенства h_х/у = 0 не следует h_у/х = 0 и наоборот.

Всегда h ³ | r |, причем в случае линейной корреляционной зависимости h=|r| и h_х/у = h_у/х. Чем хуже выполняются указанные соотношения, тем больше нелинейная зависимость у от х.