Изнашивание элементов машин

При проведении предварительных исследований трения и изнашивания элементов машин с целью выявления значимости определяющих факторов широко применяют экспертные методы, позволяющие получить необходимые данные в кратчайшие сроки и без проведения испытаний.

Методы экспертной оценки чаще всего используют в ситуациях, когда достоверность исходной информации невелика. Эти методы являются вероятностными. Они основаны на способности специалиста давать полезную информацию в условиях неопределенности. Неизвестная количественная характеристика — фактор, определяющий процессы трения и изнашивания, — рассматривается в таких условиях как случайная величина, отражением закона распределения которой является индивидуальная оценка достоверности или значимости того или иного события. Когда такие оценки получены от группы экспертов, предполагается, что «истинное» значение исследуемой характеристики находится внутри диапазона оценок и что «обобщенное» коллективное мнение является более достоверным.

Выявление характера распределения оценок, полученных от группы экспертов, является трудной задачей вследствие того, что, во-первых, таких оценок обычно мало, и, во-вторых, сложно выбирать критерий, необходимый для сравнения полученной выборки с генеральной совокупностью. Поэтому чаще всего для анализа группового мнения используют различные параметры совокупности, в частности, средние значения (среднее арифметическое, медиана и т. д.), а также показатели амплитуды колебаний индивидуальных оценок относительно этой величины (среднее абсолютное отклонение, среднее квадратическое отклонение и др.):

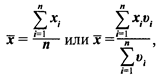
где υ₁,; υ₂; υ₃; ... υ_n — веса оценок.

Оценки, полученные от экспертов, могут быть упорядочены, т. е. расположены в порядке возрастания или убывания показателя. В случае, если необходимо установить значение показателя, которое находится в середине упорядоченного ряда, рассчитывают медиану. Медиану можно предпочесть средней арифметической, так как на нее меньшее влияние оказывают крайние точки ряда. Кроме того, в большинстве случаев медиана оказывается более устойчивой и менее подверженной случайностям подбора экспертов, чем средняя арифметическая.

При анализе экспертных оценок особенно важна вариация зна­чений около средней, поскольку чем меньше рассеяны оценки, тем точнее средние будут отражать групповое мнение. Для приближенной характеристики вариации ряда может быть вычислена амплитуда

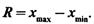
Для упорядоченного ряда могут быть рассчитаны квартили, т. е. значения признака в распределении (Q₁,, Q₂и Q₃), выбранные так, что 25 % оценок оказываются ниже Q₁, (меньше его), 25 % заключены между Q₁ и Q₂, 25 % — между Q₂ и Q₃, а остальные 25 % превосходят Q₃. Если величины квартилей приближаются к медиане, то это означает, что распределение оценок характеризуется малым рассеиванием. Следовательно, за показатель вариации принимается отклонение квартилей от медианы. Медиану применяют в случаях, когда существуют значительные колебания в оценках, полученных от разных экспертов. В остальных случаях используют среднюю арифметическую оценку.

При организации опроса экспертов важно по возможности уменьшить психологическое влияние причин, снижающих эффективность экспертных решений (взаимное убеждение, влияние авторитетов и т. п.). Организацию процедуры опроса обычно проводят в такой пос­ледовательности: подбор специалистов экспертов; разработка способа и процедуры опроса экспертов; проведение опроса; анализ информа­ции, полученной от экспертов; синтез объективной (статистической) и субъективной информации с целью подготовки оценок, необходимых для принятия решения.

На первом этапе организации опроса составляется список лиц, компетентных в рассматриваемых вопросах. Рациональное число специалистов, привлекаемых к ранжированию, составляет от 6 до 15. При этом, если вероятность правильного суждения каждого специалиста Р = 0,7, то вероятность того, что все специалисты примут это решение, составляет: при пяти специалистах Р = 0,525, при семи специалистах Р = 0,647, при десяти специалистах Р = 0,650.

Таким образом, при возрастании числа специалистов от 7 до 10 вероятность принятия определенного решения всеми специалистами увеличивается незначительно.

Кандидатам в экспертную группу предлагается заполнить анкеты. Ответ на каждый из поставленных в анкете вопросов дается в короткое время (5—10 мин); кроме того, делается «самооценка» своих знаний в данной области по 5—10-балльной системе. Подобные анкеты позволяют судить как о действительных знаниях эксперта, так и о его способности критически оценить собственные возможности.

Существует несколько способов проведения опроса экспертов. Один из них, метод согласования, заключается в том, что каждый эксперт дает оценку независимо от других, а затем, с помощью какого-либо приема, эти оценки объединяются в одну обобщенную (согласованную).

Второй способ (групповой) основан на совместной работе экспертов и получении суммарной оценки от всей группы в целом.

При третьем способе (метод Делфи) согласование индивидуальных оценок сочетается с последовательным ознакомлением каждого эксперта с оценками остальных. Наиболее распространен опрос группы экспертов по методу согласования оценок. В этом случае обобщенная оценка

средняя взвешенная оценка

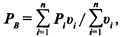
где Р_i — оценка i-го эксперта; n — число экспертов; υ_i — вес мнения, приписываемый i-му эксперту; P_i — оценка i-го эксперта.

Вес мнения каждого эксперта определяется либо на основе оце­нок предыдущей деятельности эксперта, например, степени надежнос­ти, либо с учетом квалификации, эрудиции, должности или академи­ческого звания эксперта.

Опрос можно проводить заочно, когда личный контакт аналити­ков с экспертами отсутствует, или очно, когда заполнение анкеты осу­ществляется при личной беседе с экспертом. Преимуществами заочного опроса является его относительная простота и низкая стоимость, одна­ко в этом случае возможны ошибки при заполнении анкет. При личной беседе этот недостаток исключается, но требуются значительные затраты труда и времени. Кроме того, аналитик, проводящий личный опрос, может сознательно или невольно влиять на ответы эксперта.

При заполнении анкет определенную роль играет порядок пос­тановки вопросов и их фразеологическая формулировка. Установлено, что сначала лучше требовать ответы на наиболее сложные и общие вопросы, а затем постепенно переходить к более простым и частным. При этом следует формулировать вопросы так, чтобы исключить возможность двойного толкования (двусмысленность).

Иногда рекомендуется проводить опрос экспертов в несколько туров. Это позволяет экспертам «взвесить» свои суждения с учетом ответов и доводов коллег и дополнительной информации, которая не была учтена в предыдущем туре.

Данные, полученные в результате экспертной оценки значимости факторов, обрабатывают в такой последовательности:

1)вычисляют сумму рангов 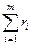для каждого фактора;

2)определяют среднее значение суммы рангов по всем факторам и для всех экспертов

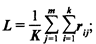
3) вычисляют отклонение суммы рангов каждого фактора от об­щего среднего ранга

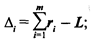
4) определяют сумму квадратов отклонений

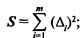
5) в зависимости от суммы рангов каждому показателю присваивают общий ранг;

6) проверяют степень согласованности мнений экспертов с помощью критерия Кендалла, называемого коэффициентом конкордации,

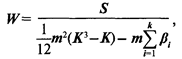
где m — число экспертов; К — число ранжируемых факторов; β_i — коэффициент, зависящий от компетенции специалистов,

[n_ij— число показателей, которым i-й эксперт присвоил одинаковый ранг].

Коэффициент конкордации подчиняется χ²-распределению. Гипотеза о наличии согласованности мнений специалистов принимается при выполнении условия m (К–1) W > 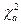(K – 1) [здесь 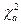(К – 1) — квантиль χ²-распределения, соответствующий уровню значимости а и числу степеней свободы (К–1)]. На основании результатов ранжирования получают математическую модель

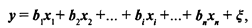
где b_i — коэффициент, характеризующий уровень значимости фактора; х_i — фактор, влияние которого на изменчивость признака у признается существенным; ξ— величина, характеризующая шумовое поле: 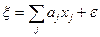(ε — погрешность результатов).

Коэффициенты b_i определяют следующим образом: вычисляют относительный уровень значимости факторов

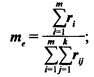
определяют удельный вес каждого фактора q_i = 1 - m_е100; вычисляют коэффициент значимости каждого фактора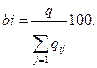

Пример. Необходимо оценить значимость факторов, определяющих характер трения и изнашивания фрикционных элементов тормоза.

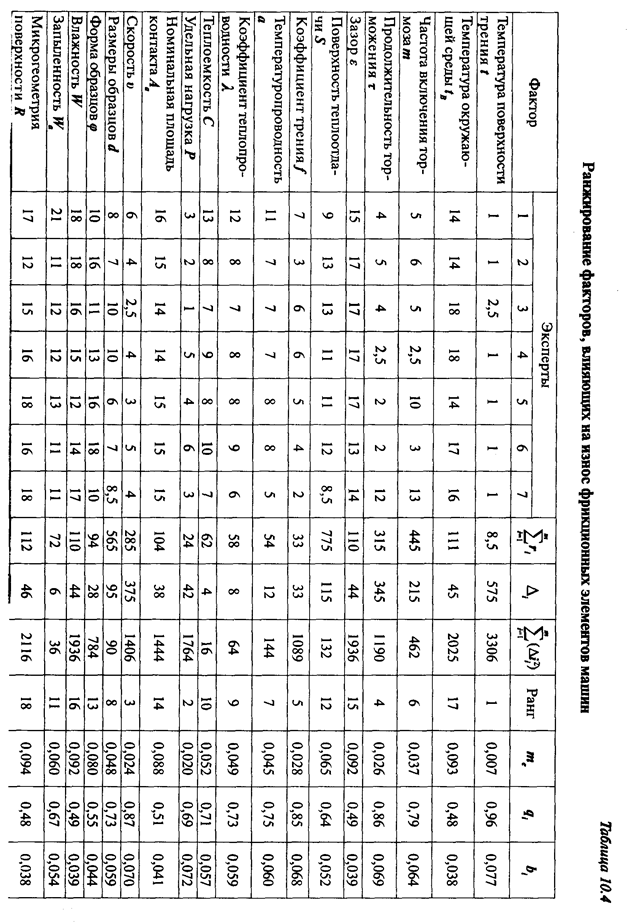
Из литературных источников известно, что на интенсивность изнашивания фрикционных элементов оказывают влияние факторы, перечень которых приведен в табл. 13.4. Данные, полученные при опросе экспер­тов, и промежуточные результаты расчетов также сведены в табл. 13.3.

Анализ результатов ранжирования и значений коэффициентов b_i позволяет отсеить факторы, влияние которых на изменчивость признака несущественно. Приближенная математическая модель имеет следующий вид:

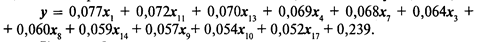
Таким образом, в результате экспертной оценки значимости факторов, влияющих на интенсивность изнашивания фрикционных элементов машин, произведено ранжирование факторов и выявлены те из них, влияние которых на изменчивость признака И наиболее значи­тельно. К этим факторам относятся: х₁ = t; x₁₁ = Р; х₁₃ = υ; х₄ = τ; х₃ = m; х₇ = f; х₈ = а; х₉ = λ; х₁₀ = С; х₁₄ = d; x_l = S.