Физическое моделирование процессов изнашивания

Для того чтобы получить достоверные результаты исследований трения и изнашивания, необходимо обеспечить взаимно однозначное соответствие между процессами, происходящими в сборочных единицах машин при испытаниях, и аналогичными процессами в условиях эксплуатации. Это возможно при использовании физического моделирования.

Физическое моделирование — метод исследования, позволяющий получить необходимые сведения об изучаемом объекте с помощью испытаний другого более простого объекта, называемого моделью. Отличи­тельной особенностью физического моделирования является общая физическая природа явлений, происходящих в изучаемом объекте и модели. В основе моделирования лежит подобие изучаемого объекта и модели.

Подобием называется взаимно однозначное соответствие между изучаемым объектом и моделью, при котором функции перехода от параметров, характеризующих объект, к соответствующим параметрам модели известны, а математические описания объекта и модели могут быть преобразованы в тождественные.

Физическое моделирование базируется на теории подобия. Положения теории подобия позволяют правильно ставить эксперимент, распространять результаты исследований одного объекта на множество подобных ему систем; выбирать параметры модели так, чтобы моделируемые процессы были тождественны соответствующим процессам в системе-оригинале.

В соответствии с основными положениями теории подобия не­обходимыми и достаточными условиями подобия изучаемого объекта и модели являются пропорциональность сходственных параметров, определяющих характер протекания явлений и входящих в условия од­нозначности, и равенство критериев подобия — безразмерных соотно­шений определяющих параметров, т. е. если изучаемый объект описы­вается выражением у₁ = φ₁(А₁; Б₁; В₁; Г₁;....), а описание модели можно представить в виде у₂ = φ₂ (А₂; Б₂; В₂; Г₂;....), то объект и модель подоб­ны, если А₁= С_АА₂; Б₁ = С_ББ₂; В₁ = С_ВВ₂; Г₁ = С_ГГ₂ и А₁Б₁/В₁ = А₂Б₂/В₁; В₁/Г₁ = В₂/Г₂.

Критерии подобия можно определить двумя методами: с помощью анализа систем уравнений; с помощью анализа размерностей определяющих факторов.

Эти методы дают сходные результаты. Определение критериев подобия на основе уравнений позволяет получить более обоснованные результаты. Однако при исследовании достаточно сложных систем, не имеющих математического описания, этот метод неприменим. Тогда используют метод анализа размерностей. При физическом моделировании часто применяют оба метода.

При исследовании трения и изнашивания элементов дорожных машин, применяя физическое моделирование, необходимо выдерживать следующую последовательность операций: первое — определить показа­тели режима работы механизма (по результатам эксплуатационных, поли­гонных и теоретических исследований); второе — сформировать условия подобия на основе теоретического анализа изнашивания и определить условия подобия изнашивания элементов машин и условия приближен­ного физического моделирования; третье — по результатам, полученным на первой и второй стадиях, разработать методики приближенного физического моделирования изнашивания элементов машин; укомплектовать стенд физического моделирования; сформулировать физические модели изнашивания элементов машин; провести экспериментальные исследова­ния на стенде физического моделирования; провести обработку и анализ результатов и определить закономерности изменения элементов машин и погрешности физического моделирования.

Условия физического моделирования трения и изнашивания эле­ментов машин вытекают из условий подобия рассматриваемых явлений и заключаются в том, что должны быть:

• численно равные определяющие критерии подобия изнашивания для модели и изучаемого объекта;

• соответственно пропорциональны для модели и объекта одно­именные физические параметры исходного определительного уравнения;

• геометрически подобны модель и объект;

• соблюдено при формировании модели кинематическое подобие;

• соответственно подобны начальные условия, характеризующие изнашивание на модели, и изучаемый объект;

• подобны граничные условия модели и граничные условия объекта исследования;

• соблюдено для модели и объекта тождество совместных плотностей распределения определяющих критериев подобия, обеспечивающее подобие явлений в вероятностном смысле, с учетом возможных отклонений случайных величин.

Формирование критериев подобия методом анализа уравнений проводят на основе математического описания явления изнашивания. Существует три метода определения критериев подобия на основе анализа уравнений: метод подобных преобразований, метод интегральных аналогов, метод приведения уравнений к безразмерному виду. Наиболее простым и распространенным является метод интегральных аналогов. Этот метод основан на правиле замещения, согласно которому в случае подобия явлений вместо производных любого порядка от характерных величин можно рассматривать отношения соответствующих величин.

Определение критериев подобия методом интегральных аналогов проводят в такой последовательности:

• дифференциальные уравнения, входящие в состав математического описания явлений, записывают в форме интегральных аналогов;

• одновременно все входящие в уравнение компоненты векторов по осям координат заменяют абсолютными значениями векторов, а координаты заменяют характерным линейным размером системы;

• интегральные аналоги приводят к безразмерному виду путем деления на один из членов уравнения;

• анализируют сформированные критерии подобия.

При исследовании сопряжений машин, для которых математичес­кое описание изнашивания еще не получено, формирование критериев подобия проводят методом анализа размерностей. В качестве примера рассмотрим порядок определения критериев подобия изнашивания применительно к фрикционным элементам.

Пример. Для прогнозирования ресурса фрикционных элементов колодочного тормоза на стадии проектирования необходимо определить закономерность изнашивания рабочих поверхностей фрикционных накладок в процессе работы. С целью обоснования режимов испытаний образцов на стенде необходимо установить условия физического моделирования, сформировать критерии подобия.

Определение критериев подобия на основе анализа уравнений. Для выявления безразмерных соотношений параметров, входящих в математическое описание явления изнашивания, необходимо представить уравнения в форме интегральных аналогов, опустив знаки опера­торов. Система основных уравнений изнашивания элементов машин состоит из выражений, характеризующих процессы, сопровождающие рассматриваемое явление.

Процесс распространения теплоты в твердом теле характеризуется уравнением Фурье

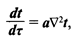(13.1)

где t — температура твердого тела, °С; а — коэффициент температуропроводнсти, определяющий темп процес­са перестройки температурного поля, а = λ/Ср; С— теплоемкость материала; р — плотность материала; λ — теплопроводность; Δ² — оператор Лапласа, т. е. символ, обозначающий операцию суммиро­вания вторых производных от скалярной величины по координатам.

Это уравнение получено на основе закона сохранения и пре­вращения энергии, в соответствии с которым изменение внутренней энергии элемента должно равняться количеству теплоты, отводимому в окружающую среду.

Уравнение (13.1) распространения теплоты в твердом теле в форме интегральных аналогов перепишем следующим образом:

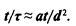(13.2)

Основное уравнение, характеризующее процесс распространения теплоты в окружающей среде, выражает закон сохранения и превращения энергии, сформулированный применительно к условиям взаимодействия элемента с окружающим воздухом. Это уравнение, называемое уравнением энергии Фурье—Кирхгофа, записываем следующим образом:

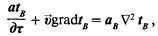(13,3)

где t_в и a_в — соответственно температура и температуропроводность воздуха.

Уравнение распространения теплоты в окружающей среде в форме интегральных аналогов имеет следующий вид:

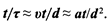(13.4)

Поделив соотношения (13.2) и (13.4) на t/τ, получим следующую систему безразмерных соотношений из выражения (13.2): 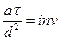; из выражения (13.4)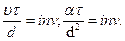

Комплекс , 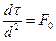называемый критерием Фурье, характеризует временное подобие сопоставляемых тепловых явлений. При распространении теплоты в твердом теле, когда скорость протекания подобных процессов зависит исключительно от величин, определяющих геометрические d и физические, а свойства тела, критерий Фурье выражает влияние этих величин на темп развития явления. Все подобные явления характеризуются одним и тем же значением критерия F_o. Таким образом, равенство значений этого критерия является необходимым условием подобия явлений.

VX

Комплекс 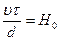— критерий гомохронности — показывает, что подобие распределения скоростей на границах системы должно устанавливаться в сходственные моменты времени; иначе говоря, в подобных системах изменение кинематических условий должно происходить гомохронно.

Анализ полученных критериев показывает, что ни один из них не содержит температуры. Это объясняется тем, что исходные дифферен­циальные уравнения (13.1) и (13.3) однородны относительно температу­ры, вследствие чего при формировании безразмерных комплексов она сокращается. Таким образом, температура может входить в уравнение подобия только в виде симплекса t/t₀ (здесь t₀ — средняя температура на поверхности трения в начальный момент торможения).

Математического описания процесса пластического деформирования, сопровождающего изнашивание элементов машин, в настоящее время не существует. Результаты исследований показывают, что характер этого процесса достаточно полно определяется коэффициентом трения и схемой фрикционного контакта. Следовательно, процесс пластического деформирования при изнашивании может быть косвенно учтен через за­висимости износа от коэффициента трения И = φ (f). Это функциональное выражение характеризует, кроме того, влияние на износ микрогеометрии поверхности и физико-механических свойств материала пары трения.

Отделение частиц материала (продуктов износа) с поверхности трения является заключительным этапом в последовательности процессов, сопровождающих изнашивание. Механизм разрушения твердых тел в основном зависит от вида материала, характера нагружения и нагрузки, вызывающей разрушение. Зависимость линейного износа от удельной нагрузки, полученная на основе закона сохранения энергии, в дифференциальной форме записывается следующим образом:

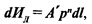(13.5)

где А' — коэффициент, зависящий от вида материала и характера нагружения; n — показатель степени.

Уравнение (13.5) в общем виде описывает механизм разрушения твердых тел, в результате которого образуются продукты износа. Из уравнений (13.4), (13.5) можно получить следующие инвариантные соотношения:

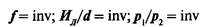
(здесь индексы 1, 2 означают принадлежность параметра к одному из сопоставляемых процессов).

Полученные инвариантные соотношения приводят к крите­риям подобия: f— критерий, определяющий подобие фрикцион­ных свойств материалов трущихся тел и вида фрикционной связи; критерий И_л/d представляет собой отношение линейного износа к определяющему параметру и характеризует интенсивность изна­шивания материала; критерий р₁/р₂ определяет условия нагружения при изнашивании.

Система основных уравнений (13.1)—(13.5) представляет собой об­щее математическое описание изнашивания элементов машин в условиях трения без смазочного материала, основанное на анализе его физической сущности. Все основные уравнения получены на базе фундаментальных законов физики (закона сохранения и превращения энергии, закона сохранения массы), поэтому их справедливость не вызывает сомнения. Однако необходимо учитывать, что приведенные уравнения описывают рассматриваемое явление лишь в наиболее общем виде, определяя только свойства, характерные для всего класса явлений изнашивания.

Общая система критериев подобия изнашивания фрикционных элементов машин, полученная на основе математического описания, имеет следующий вид;

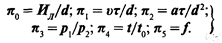
Формирование критериев подобия изнашивания методом анализа размерностей. По результатам предварительных исследований и литературным данным выявляют факторы, определяющие характер процесса изнашивания фрикционных элементов машин. Запишем общую функциональную зависимость в виде

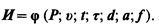
Затем необходимо составить таблицу размерностей определяющих факторов (табл. 13.3). В качестве основных выбираем единицы размерности массы М, времени Т, длины L, температуры θ.

Выражение (13.6) можно переписать в следующем виде:

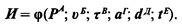(13.7)

Безразмерный параметр f при этом из рассмотрения исключается.

Подставим в полученное выражение вместо параметров их раз­мерность в соответствии с формулами, приведенными в табл. 13.2:

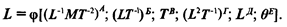
Размерности определяющих факторов

Таблица 13.3

Параметр	Обозначения	Формула размерности
Удельная нагрузка	Р	L-1МT-2
Скорость	υ	LT-1
Температура	t	θ
Продолжительность испытаний	τ	Т
Коэффициент трения	f	-
Износ линейный	Ил	L
Определяющий параметр	d	L
Температуропроводность	а	L2T-1

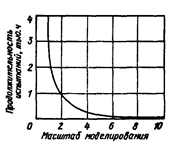
Рис. 13.21. Зависимость продолжительности испытаний образцов от масштаба моделирования

Чтобы данное уравнение было однородным относительно раз­мерностей, между показателями степени должны выполняться следующие соотношения:

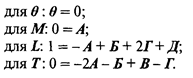
Таким образом, получилось три уравнения с пятью неизвестны­ми. Упростим их, исключив А, В и Д. А = 0; В = Б + Г; Д = 1– Б – 2Г. Подставим эти соотношения в формулу (13.7):

Объединяя члены с одинаковыми показателями степени, можно составить следующие безразмерные комбинации: π₀ = И/d; π₁ = аτ/d²; π₂ = υτ/d.

Безразмерный параметр f также принимают в качестве критерия подобия π₃= f.

Влияние удельной нагрузки и температуры на протекание процесса изнашивания учитывается симплексами: π₄ = P₁/P₂; π₅ = t/t₀.

Подобие рассматриваемой системы обеспечивается инвариантностью полученных П-критериев.

Таким образом, анализ размерностей определяющих факторов позволил сформировать те же критерии подобия, которые были получены на основе анализа уравнений.

Условия приближенного физического моделирования изнашивания фрикционных элементов машин на основании полученных критериев подобия записываются следующим образом:

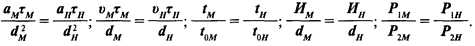
В приведенных соотношениях индекс М означает принадлежность фактора модели, а индекс Н— изучаемому объекту, называемому натурой.

Из условий приближенного физического моделирования выводят аналитические зависимости, с помощью которых можно осуществить пересчет значений определяющих факторов с натуры на модель:

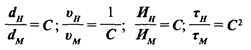
(здесь С— масштаб моделирования).

Полученные зависимости позволяют строго обосновать режимы испытаний при исследовании изнашивания фрикционных элементов машин. График зависимости продолжительности испытаний от мас­штаба моделирования приведен на рис. 13.21. Из графика видно, что при масштабе моделирования С = 4 продолжительность эксперимен­тальных исследований в 16 раз меньше продолжительности исследова­ний объекта в натуральную величину на специализированном стенде. С увеличением масштаба моделирования это соотношение еще более увеличивается, но при этом значительно возрастает погрешность моделирования и нарушаются условия изнашивания.