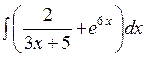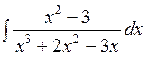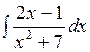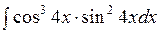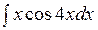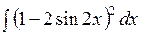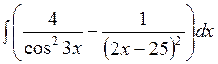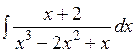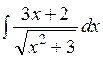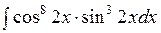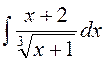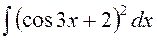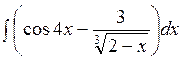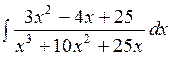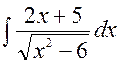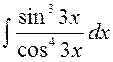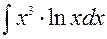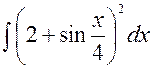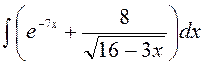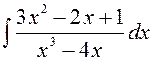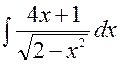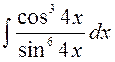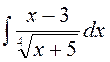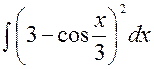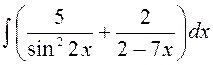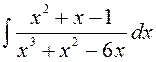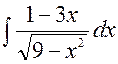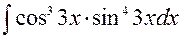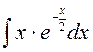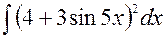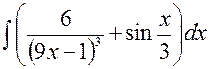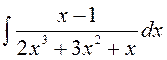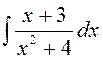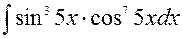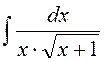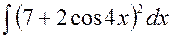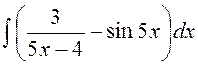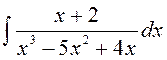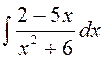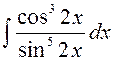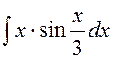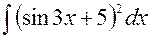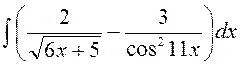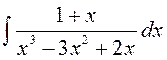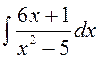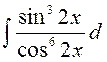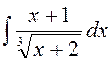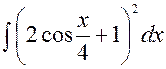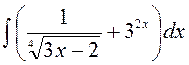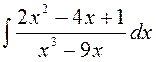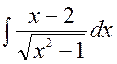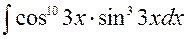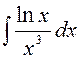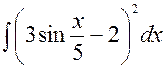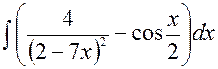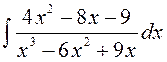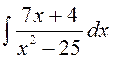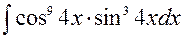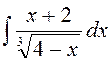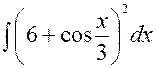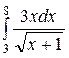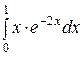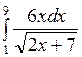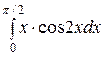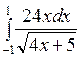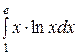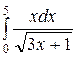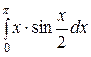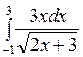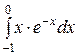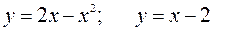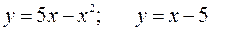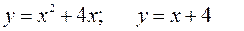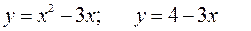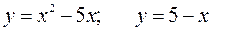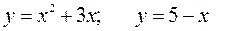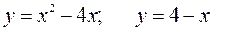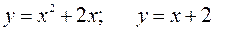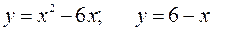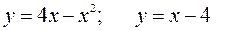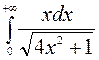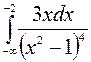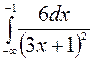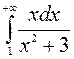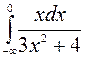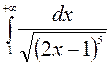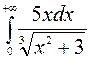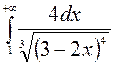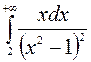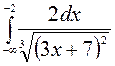| № варианта | Номера задач контрольных работ |
| Номер контрольной работы |
| | |
| | 1(б, в, д) | | | | 81(а) | | | | | 141(а,б,в,г,е) |
| | 2(б, в, д) | | | | 82(а) | | | | | 142(а,б,в,г,е) |
| | 3(б, в, д) | | | | 83(а) | | | | | 143(а,б,в,г,е) |
| | 4(б, в, д) | | | | 84(а) | | | | | 144(а,б,в,г,е) |
| | 5(б, в, д) | | | | 8(а) | | | | | 145(а,б,в,г,е) |
| | 6(б, в, д) | | | | 86(а) | | | | | 146(а,б,в,г,е) |
| | 7(б, в, д) | | | | 87(а) | | | | | 147(а,б,в,г,е) |
| | 8(б, в, д) | | | | 88(а) | | | | | 148(а,б,в,г,е) |
| | 9(б, в, д) | | | | 89(а) | | | | | 149(а,б,в,г,е) |
| | 10(б, в, д) | | | | 90(а) | | | | | 150(а,б,в,г,е) |
| № варианта | Номера задач контрольных работ |
| Номер контрольной работы |
| | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | |
Задания для контрольных работ
Предел и непрерывность функции
Контрольная работа № 1
1—10.Найти пределы функций (не пользуясь правилом Лопиталя).
| | а | 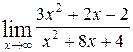 | г | 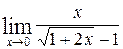 |
| б | 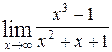 | д | 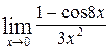 |
| в | 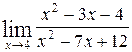 | е | 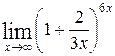 |
| | а | 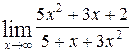 | г | 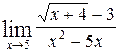 |
| б | 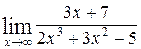 | д | 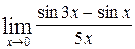 |
| в | 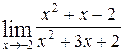 | е | 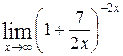 |
| | а | 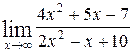 | г | 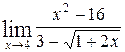 |
| б | 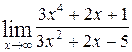 | д | 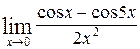 |
| в | 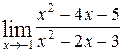 | е | 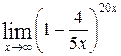 |
| | а | 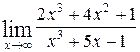 | г | 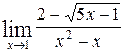 |
| б | 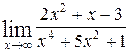 | д | 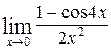 |
| в | 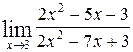 | е | 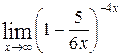 |
| | а | 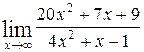 | г | 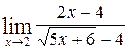 |
| б | 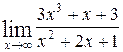 | д | 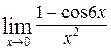 |
| в | 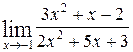 | е | 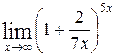 |
| | а | 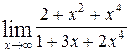 | г | 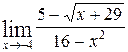 |
| б | 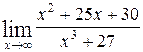 | д | 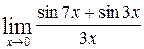 |
| в | 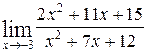 | е | 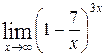 |
| | а | 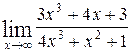 | г | 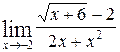 |
| б | 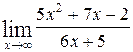 | д | 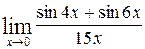 |
| в | 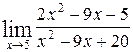 | е | 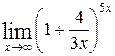 |
| | а | 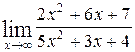 | г | 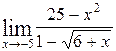 |
| б | 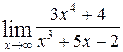 | д | 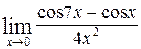 |
| в | 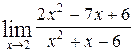 | е | 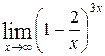 |
| | а | 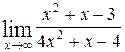 | г | 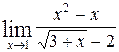 |
| б | 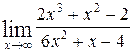 | д | 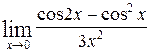 |
| в | 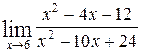 | е | 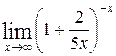 |
| | а | 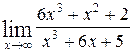 | г | 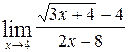 |
| б | 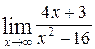 | д | 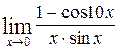 |
| в | 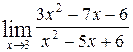 | е | 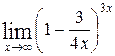 |
11—20.Задана функция 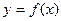 и два значения аргумента
и два значения аргумента 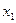 и
и 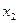 . Установить, является ли данная функция непрерывной или разрывной для каждого из данных аргументов; в случае разрыва функции найти ее пределы в точке разрыва слева и справа и установить, какого рода разрыв.
. Установить, является ли данная функция непрерывной или разрывной для каждого из данных аргументов; в случае разрыва функции найти ее пределы в точке разрыва слева и справа и установить, какого рода разрыв.
21—30. Задана функция  . Найти точки разрыва функции, если они существуют, определить характер разрыва, сделать чертеж.
. Найти точки разрыва функции, если они существуют, определить характер разрыва, сделать чертеж.
Производная и дифференциал функции одной переменной
Контрольная работа № 2
31—40. Найти производные 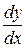 следующих функций:
следующих функций:
| | а) | 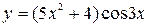 | | а) | 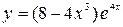 |
| б) | 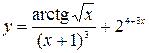 | б) | 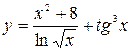 |
| в) | 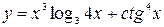 | в) | 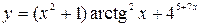 |
| | а) | 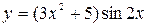 | | а) | 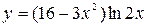 |
| б) | 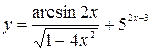 | б) | 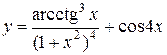 |
| в) | 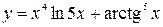 | в) | 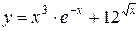 |
| | а) | 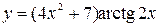 | | а) | 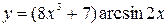 |
| б) | 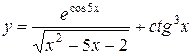 | б) | 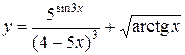 |
| в) | 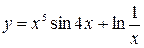 | в) | 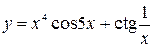 |
| | а) | 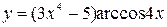 | | а) | 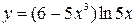 |
| б) | 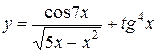 | б) | 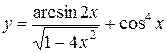 |
| в) | 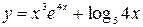 | в) | 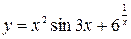 |
| | а) | 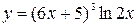 | | а) | 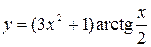 |
| б) | 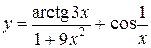 | б) | 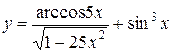 |
| в) | 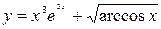 | в) | 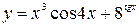 |
41—50.Записать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой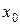 .
.
51—60.Найти 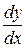 и
и 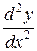 для заданной функции.
для заданной функции.
61—70.Найти 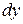 .
.
Приложения производной
Контрольная работа № 3
71— 80. Найти пределы функций, используя правило Лопиталя.
| | а) 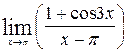 | б) 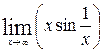 |
| | а) 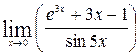 | б) 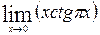 |
| | а) 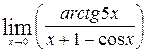 | б) 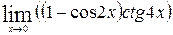 |
| | а) 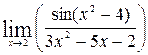 | б) 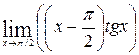 |
| | а) 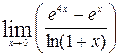 | б) 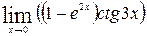 |
| | а) 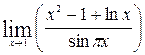 | б) 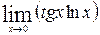 |
| | а) 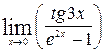 | б) 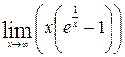 |
| | а) 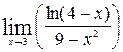 | б) 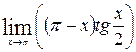 |
| | а) 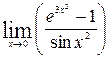 | б) 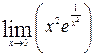 |
| | а) 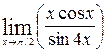 | б) 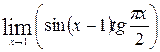 |
81—90. Исследовать методами дифференциального исчисления функцию 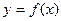 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
| | а) 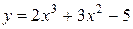 | б) 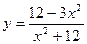 |
| | а) 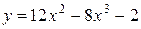 | б) 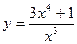 |
| | а) 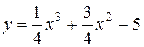 | б) 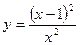 |
| | а) 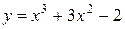 | б) 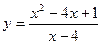 |
| | а) 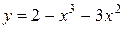 | б) 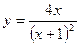 |
| | а) 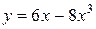 | б) 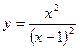 |
| | а) 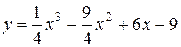 | б) 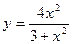 |
| | а) 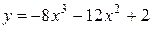 | б) 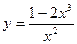 |
| | а) 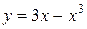 | б) 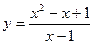 |
| | а) 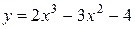 | б) 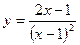 |
91—100. Найти наибольшее и наименьшее значение функции 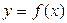 на отрезке
на отрезке 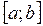 .
.
Функции нескольких переменных
Контрольная работа № 4
101—110.Найти вторые частные производные указанных функций. Убедиться в том, что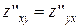 .
.
111—120.Исследовать на экстремум следующие функции.
121—130.Дана функция 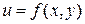 , точка
, точка 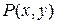 и вектор
и вектор 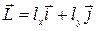 . Найти: а)
. Найти: а) 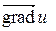 в точке А; б) производную в точке А по направлению вектора
в точке А; б) производную в точке А по направлению вектора 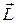 .
.
| | 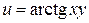 | P(2;2) | 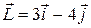 |
| | 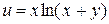 | P(-1;2) | 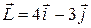 |
| | 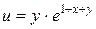 | P(0;-1) | 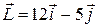 |
| | 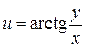 | P(1;1) | 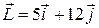 |
| | 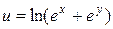 | P(0;0) | 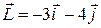 |
| | 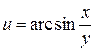 | P(0;1) | 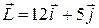 |
| | 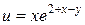 | P(1;1) | 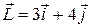 |
| | 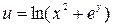 | P(1;0) | 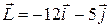 |
| | 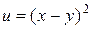 | P(0;3) | 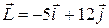 |
| | 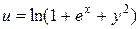 | P(0;1) | 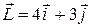 |
131—140.Полагая, что меду переменными x и y существует линейная зависимость, найти эмпирическую формулу 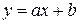 методом наименьших квадратов по следующим данным.
методом наименьших квадратов по следующим данным.
Неопределенный и определенный интегралы
Контрольная работа № 5
141—150. Найти неопределенные интегралы.
| | а | 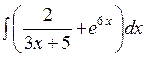 | г | 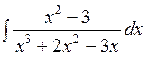 |
| б | 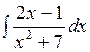 | д | 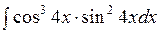 |
| в | 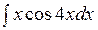 | е | 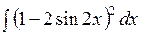 |
| | а | 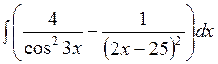 | г | 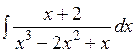 |
| б | 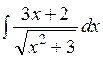 | д) | 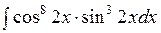 |
| в | 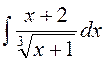 | е | 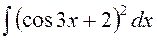 |
| | а | 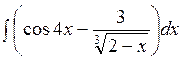 | г | 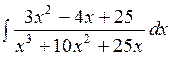 |
| б | 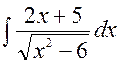 | д | 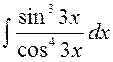 |
| в | 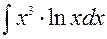 | е | 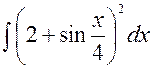 |
| | а | 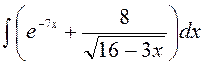 | г | 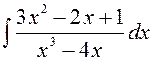 |
| б | 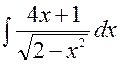 | д | 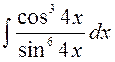 |
| в | 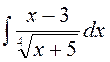 | е | 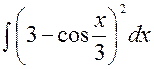 |
| | а | 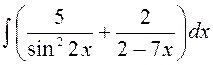 | г | 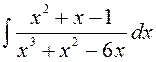 |
| б | 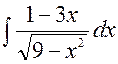 | д | 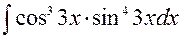 |
| в | 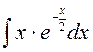 | е | 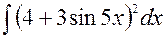 |
| | а | 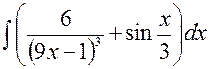 | г | 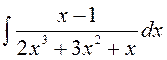 |
| б | 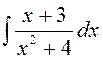 | д | 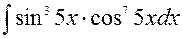 |
| в | 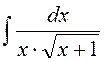 | е | 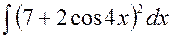 |
| | а | 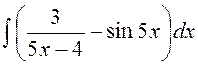 | г | 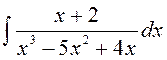 |
| б | 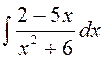 | д | 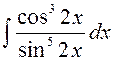 |
| в | 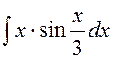 | е | 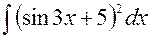 |
| | а | 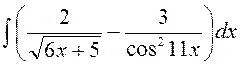 | г | 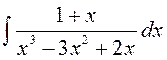 |
| б | 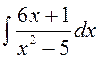 | д | 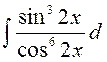 |
| в | 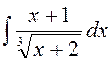 | е | 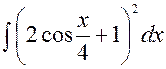 |
| | а | 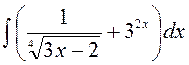 | г | 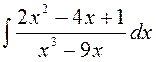 |
| б | 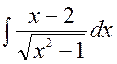 | д | 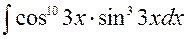 |
| в | 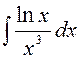 | е | 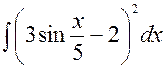 |
| | а | 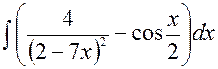 | г | 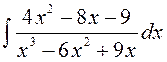 |
| б | 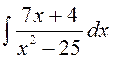 | д | 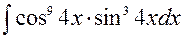 |
| в | 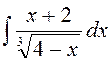 | е | 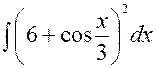 |
151— 160. Вычислить значение определенного интеграла.
161—170. Вычислить площадь фигуры, ограниченной графиками указанных функций.
171—180. Вычислить несобственный интеграл или доказать его расходимость.
Дифференциальные уравнения. Ряды
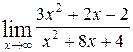
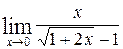
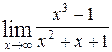
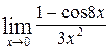
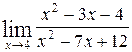
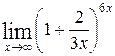
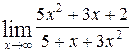
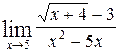
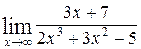
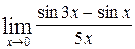
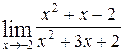
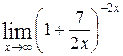
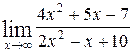
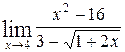
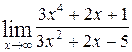
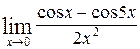
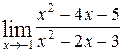
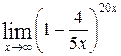
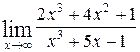
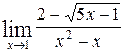
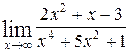
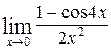
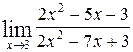
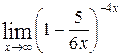
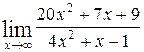
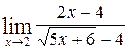
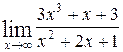
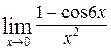
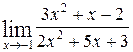
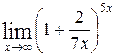
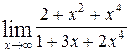
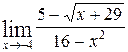
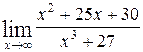
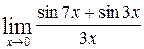
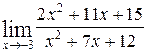
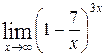
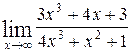
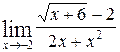
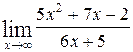
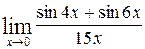
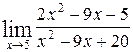
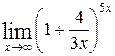
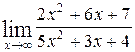
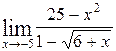
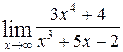
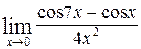
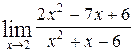
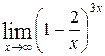
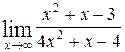
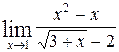
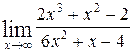
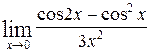
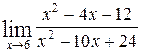
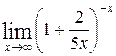
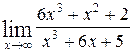
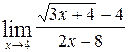
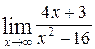
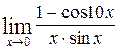
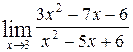
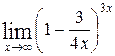
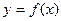 и два значения аргумента
и два значения аргумента 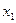 и
и 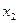 . Установить, является ли данная функция непрерывной или разрывной для каждого из данных аргументов; в случае разрыва функции найти ее пределы в точке разрыва слева и справа и установить, какого рода разрыв.
. Установить, является ли данная функция непрерывной или разрывной для каждого из данных аргументов; в случае разрыва функции найти ее пределы в точке разрыва слева и справа и установить, какого рода разрыв.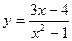
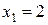
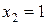
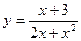
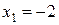
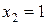
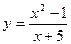
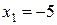
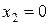
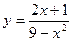
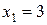
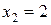
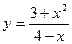
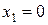
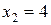
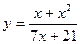
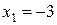
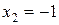
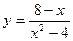
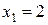
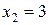
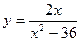
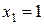
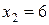
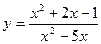
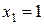
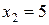
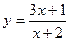
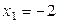
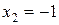
 . Найти точки разрыва функции, если они существуют, определить характер разрыва, сделать чертеж.
. Найти точки разрыва функции, если они существуют, определить характер разрыва, сделать чертеж.

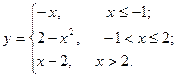
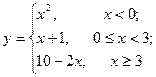
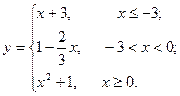
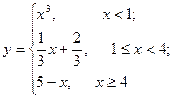
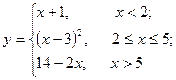
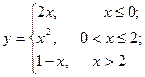
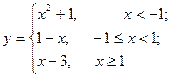
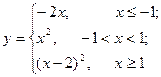
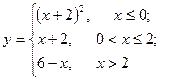
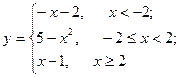
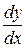 следующих функций:
следующих функций: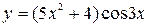
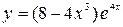
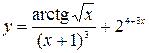
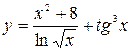
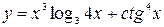
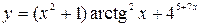
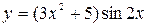
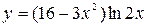
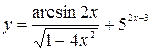
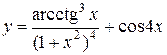
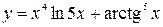
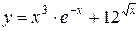
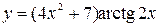
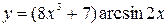
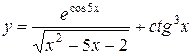
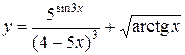
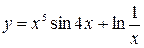
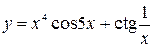
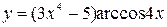
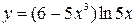
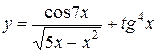
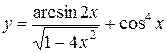
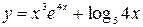
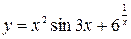
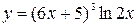
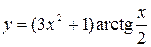
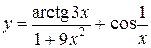
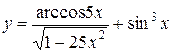
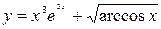
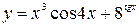
 в точке с абсциссой
в точке с абсциссой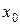 .
.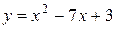
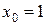
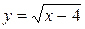
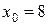
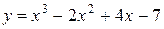
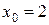
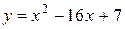
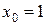
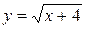
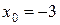
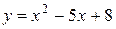
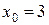
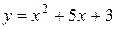
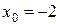
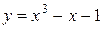
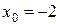
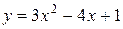
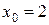
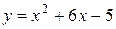
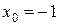
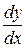 и
и 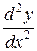 для заданной функции.
для заданной функции.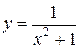
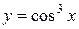
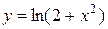
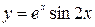
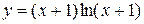
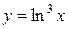
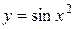
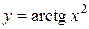
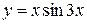
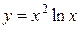
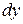 .
.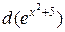
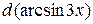
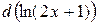
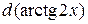
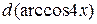
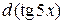
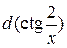
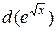
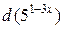
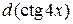
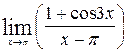
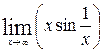
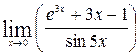
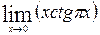
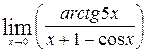
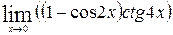
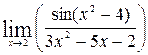
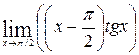
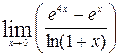
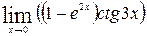
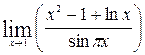
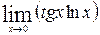
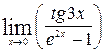
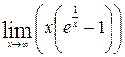
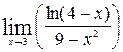
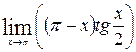
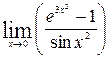
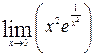
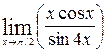
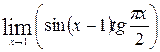
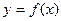 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.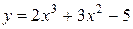
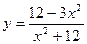
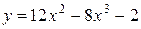
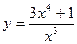
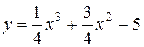
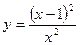
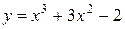
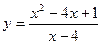
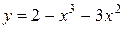
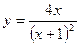
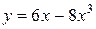
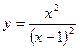
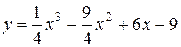
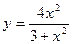
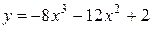
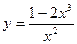
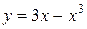
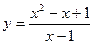
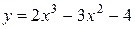
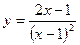
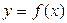 на отрезке
на отрезке 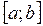 .
.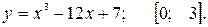
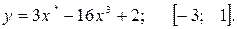
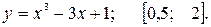
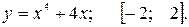
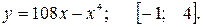
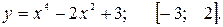
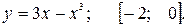
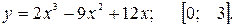
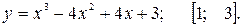
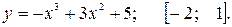
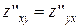 .
.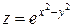
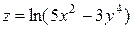
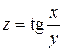
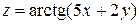
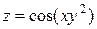
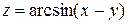
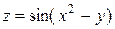
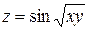
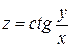
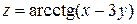
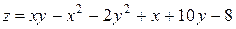
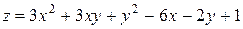
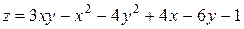
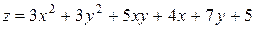
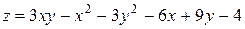
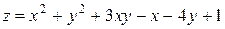
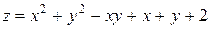
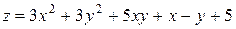
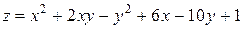
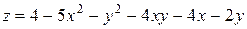
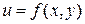 , точка
, точка 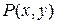 и вектор
и вектор 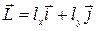 . Найти: а)
. Найти: а) 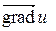 в точке А; б) производную в точке А по направлению вектора
в точке А; б) производную в точке А по направлению вектора 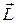 .
.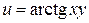
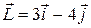
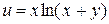
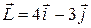
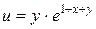
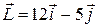
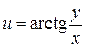
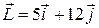
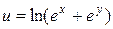
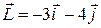
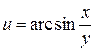
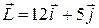
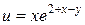
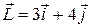
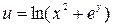
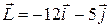
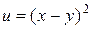
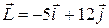
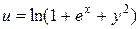
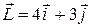
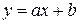 методом наименьших квадратов по следующим данным.
методом наименьших квадратов по следующим данным.