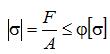Понятие о потере устойчивости при напряжениях, превышающих предел пропорциональности материала. Формула Ясинского

Тщательно поставленные опыты показали справедливость формулы Эйлера для стержней большой гибкости. В то же время эти опыты подтвердили неприменимость формулы Эйлера для стержней, гибкость которых λ<λ_o. Для таких стержней формула Эйлера дает значения критических нагрузок, превышающие их действительные значения. Попытки использовать формулу Эйлера для стержней средней и малой гибкости (λ<λ_o, σ_k>σ_пц) приводили иногда к серьезным катастрофам.

Теория устойчивости стержней за пределом пропорциональности была развита Т. Карманом (1909 г.).

Для критической нагрузки им было получено уравнение, аналогичное по структуре формуле Эйлера:

,

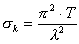(13.15)

где Т - приведенный модуль, или модуль Кармана.

Модуль Т является величиной переменной, зависящей как от величины напряжений σ_k, так и от формы сечения. Зависимость модуля Т от напряжений σ_k устанавливается на основании диаграммы сжатия материала стойки в осях σ, ε. При напряжениях σ_kЈσ_пц приведенный модуль Т принимает значение модуля упругости Е. Однако, оказалось, что определяемые формулой (13.15) критические напряжения несколько выше экспериментальных.

Лучшее согласование с экспериментальными данными дает формула Энгессера-Шенли

,

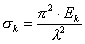(13.16)

где E_k - касательный модуль упругости, численно равный тангенсу угла наклона касательной к диаграмме сжатия σ=f(ε)материала при σ=σ_k.

Использование формул (13.15), (13.16) требует построения диаграммы сжатия для материала стержня, что осложняет их применение. Поэтому в практических расчетах на устойчивость при λ<λ_o часто пользуются либо непосредственно экспериментальными данными, либо эмпирическими формулами.

Наибольшее распространение имеет линейная формула, предложенная Ф.С. Ясинским (1895 г.):

.

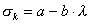(13.17)

В этой формуле λ - гибкость стержня, a и b - коэффициенты, зависящие от свойств материала. Например, для стали 3 при σ_в=380 МПа и σ_т=240 МПа формула (13.17) имеет вид

.

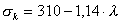По формуле (13.17) проводится расчет на устойчивость стержней средней гибкости, разрушение которых при сжатии сопровождается значительным боковым выпучиванием.

Для стержней малой гибкости (λ<λ₁) понятие потери устойчивости неприменимо в том смысле, в каком применяется для стержней большой гибкости. Стержни, у которых длина невелика по отношению к размерам поперечного сечения, выходят из строя главным образом из-за того, что напряжения сжатия в них достигают предела текучести σ_т (при пластичном материале) или предела прочности σ_в (при хрупком материале). Поэтому для стержней малой гибкости в качестве критического напряжения принимается предел текучести σ_т или предел прочности σ_в. Четкой границы между стержнями малой и средней гибкости провести нельзя. В расчетах принимают λ₁=(0.2-0.4)λ_o.

Выбрав λ₁, можно найти коэффициенты a и b в формуле (13.17), составляя уравнение прямой, проходящей через две точки с координатами (λ₁, σ_т) и (λ_o, σ_пц):

.

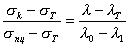Зависимость критических напряжений σ_к от гибкости λ изображается графически в виде полной диаграммы критических напряжений. Такая диаграмма для стали представлена на рис. 13.11.

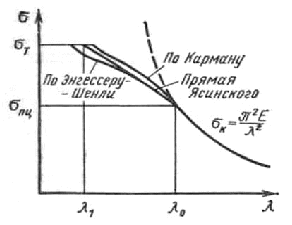
Рис. 13.11.

Для стержней малой гибкости зависимость σ_к от λ от выражена горизонтальной прямой, для стержней средней гибкости - наклонной прямой (13.17), а для стержней большой гибкости - гиперболой Эйлера.

Если известна гибкость рассчитываемого стержня, то критическое напряжение может быть найдено непосредственно по диаграмме критических напряжений.

Условие устойчивости.

Условием устойчивости сжатого стержня является неравенство:

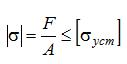
Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:

1) от длины стержня, от размеров и даже от формы поперечных сечений,

2) от способа закрепления концов стержня,

3) от материала стержня.

Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Поэтому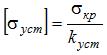

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности: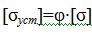

В этом случае ,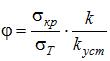

гдеσт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатиеσвс).

Коэффициент φ<1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ] по прочности, или иначе коэффициентом продольного изгиба.

С учетом сказанного условие устойчивости сжатого стержня принимает вид: