Удельная потенциальная энергия деформации. Энергия изменения объема и энергия изменения формы
В общем случае нагружения тела по граням элемента с размерами ребер dx, dy, dz будут действовать как нормальные, так и касательные напряжения. Потенциальная энергия, накопленная в этом элементе при деформации тела будет равна сумме работ внешних для выделенного элемента нормальных сил dNx=σxdydz, dNy=σydxdz, dNz=σzdxdy на удлинения ребер параллелепипеда Δdx=εxdx, Δdy=εydy, Δdz=εzdz и касательных сил dQxy=τxydydz, dQxz=τxzdxdy, dQyz=τyzdxdz на соответствующих им перемещениях γxydx, γxzdz, γyzdy граней элемента (см. рис. 3.13):
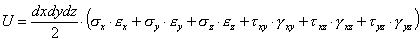 . . | (3.42) |
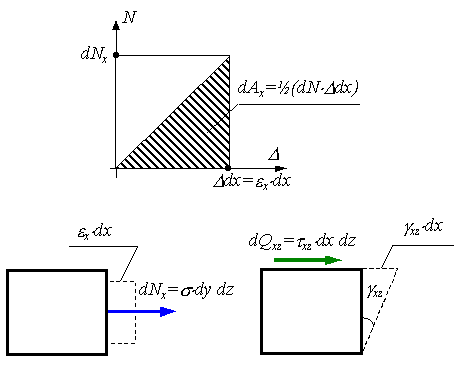
Рис. 3.13. Работа нормальных и касательных сил
Удельная потенциальная энергия, то есть энергия, накопленная в единице объема элемента, будет равна:
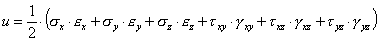 . . | (3.43) |
Если выразить компоненты деформаций через компоненты напряжений с помощью уравнений (3.36), (3.37) обобщенного закона Гука, то выражение для u запишется в следующем виде:
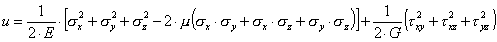 . . | (3.44) |
Предположим, что напряженное состояние в точке тела задано тензором напряжений
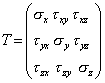 . . | (3.45) |
Представим этот тензор в виде суммы двух тензоров:
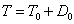 ,
,
где
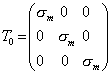 ; ; 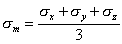 | (3.46) |
- шаровой тензор, а
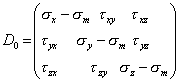 | (3.47) |
- девиатор напряжений.
Представление тензора напряжений в виде суммы двух тензоров равносильно представлению данного напряженного состояния (рис. 3.14) в виде суммы двух напряженных состояний.
Удельная потенциальная энергия деформации при всестороннем растяжении с напряжением σm определяется из уравнения (3.44):
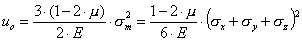 | (3.48) |
и называется удельной потенциальной энергией изменения объема, так как изменение объема зависит только от суммы нормальных напряжений (см. уравнение (3.41)).
Удельная потенциальная энергия деформации для элемента, по граням которого действуют компоненты девиатора напряжений, определяется после соответствующих преобразований из следующего уравнения:
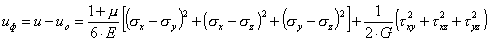 | (3.49) |
и называется удельной потенциальной энергией изменения формы. Очевидно, что удельная потенциальная энергия изменения формы в случае всестороннего растяжения с компонентами шарового тензора равна нулю. Точно также удельная потенциальная энергия изменения объема для элемента с компонентами девиатора напряжений равна нулю.
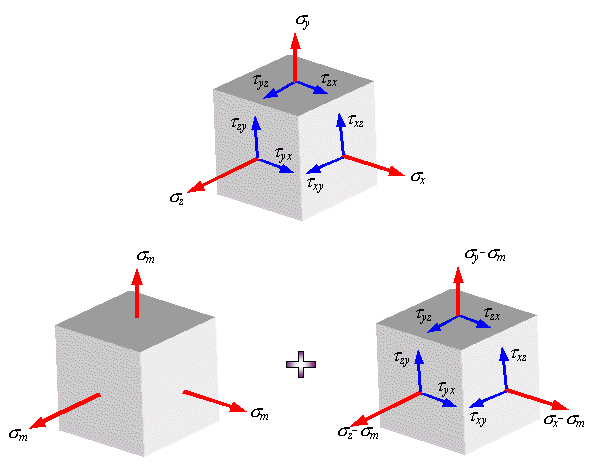
Рис. 3.14. Представление напряженного состояния в виде суммы двух напряженных состояний
Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию (V), накапливаемую в упругом теле при его деформировании.
Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения).
Таким образом, потенциальная энергия деформации стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна:
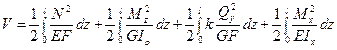 .
.
Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами). Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности. То есть принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.
