Понятие о напряженном состоянии в точке. Компоненты напряжений. Закон парности касательных напряжений
ВОПРОСЫ
К экзамену по сопротивлению материалов (часть 2)
для студентов гр. С-13з (заочная форма обучения)
Семестр 4
Метод сил раскрытия статической неопределимости (на примере изгиба балок).
Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил»
При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.
Алгоритм расчета методом сил
Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:
1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему канонических уравнений, т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Пример 1.
Построить эпюру изгибающих моментов и поперечных сил для однопролетной балки, показанной на рис. а.

Решение.
Для определения опорных реакций H, RA, RB, MA составим уравнения равновесия: 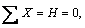 откуда H = 0, далее
откуда H = 0, далее
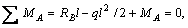 тогда
тогда 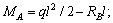
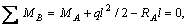 тогда
тогда 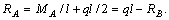
Для определения трех опорных реакций МА, RВ, RА имеем систему двух уравнений. Таким образом, задача является статически неопределимой. Для ее решения необходимо привлечь одно дополнительное уравнение 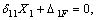 Отбросим одну лишнюю опорную реакцию RВ = Х1. В результате получим консольную балку, показанную на рис. б. Для этой полученной консольной балки строим эпюру изгибающих моментов МF от внешней нагрузки.
Отбросим одну лишнюю опорную реакцию RВ = Х1. В результате получим консольную балку, показанную на рис. б. Для этой полученной консольной балки строим эпюру изгибающих моментов МF от внешней нагрузки.
Для определения вертикального смещения 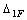 точки В построим эпюру изгибающих моментов
точки В построим эпюру изгибающих моментов  от единичной силы, приложенной в направлении отброшенной опорной реакции RB (рис. в). Затем, используя правило Верещагина, находим перемещение
от единичной силы, приложенной в направлении отброшенной опорной реакции RB (рис. в). Затем, используя правило Верещагина, находим перемещение 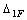 :
:
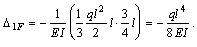
Для определения перемещения 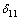 необходимо умножить по правилу Верещагина эпюру
необходимо умножить по правилу Верещагина эпюру 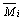 саму на себя:
саму на себя:
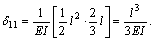
Подставим полученные результаты в формулу 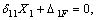 :
:
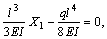 откуда
откуда 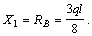
Из полученных ранее выражений определяем остальные опорные реакции:
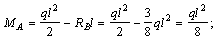
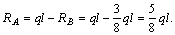
Положительные значения опорных реакций показывают, что выбранные нами предварительно их направления правильны (рис. а). Отрицательные значения показывают, что выбранные предварительно направления опорных реакций необходимо заменить на противоположные.
Проводим сечение I – I и отбрасываем мысленно левую часть, тогда
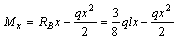 ;
; 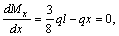 тогда
тогда 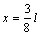 .
.
Экстремальное значение изгибающего момента в пролете будет в сечении, где поперечная сила равна нулю, т.е. на расстоянии х = 3l/8 от правой опоры:
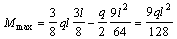 .
.
Затем строим эпюру поперечных сил:
QA = RA = 5ql/8; QB = –RB = –3ql/8.
Понятие о напряженном состоянии в точке. Компоненты напряжений. Закон парности касательных напряжений.
Напряженным состоянием в точке тела называют совокупность нормальных и касательных напряжений, возникающих на всевозможных площадках, проходящих через данную точку.
В окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные напряжения.
В зависимости от того, испытывает параллелепипед «растяжение» («сжатие») в одном, в двух или в трех направлениях, различают виды напряженного состояния:
линейное (одноосное) напряженное состояние,
плоское (двухосное) напряженное состояние,
объемное (трехосное) напряженное состояние.

Полное напряжение p  , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение
, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение  n. Здесь n – нормаль к выделенной площадке1.
n. Здесь n – нормаль к выделенной площадке1.
Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением –  nx
nx 
 ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.
ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.
p  =
= 
 n
n  nx
nx  nx
nx 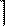
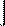
закон парности касательных напряжений:
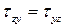
Формулировка закона парности касательных напряжений: касательные напряжения на любых двух взаимно перпендикулярных площадках, направленные по перпендикуляру к линии пересечения площадок, равны по величине, притом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от нее.
