Напряжения в поперечных сечениях бруса

При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения. Равнодействующая соответствующих элементарных сил σ_z dA - продольная сила N - может быть найдена с помощью метода сечений. Для того чтобы иметь возможность определить нормальные напряжения при известном значении продольной силы, необходимо устано­вить закон их распределения по поперечному сечению бруса.

Эта задача решается на основе гипотезы плоских сечении (гипотезы Я. Бернулли), которая гласит: сечения бруса, плоские и нормальные к его оси до деформа­ции, остаются плоскими и нормальными к оси и при деформации.

При растяжении бруса (изготовленного, например, для большей наглядности опыта из резины), на поверхности ко­торого нанесена система продольных и поперечных рисок, можно убедиться, что риски остаются прямоли­нейными и взаимно перпендикулярными, изменяются лишь расстояния: между поперечными рисками несколько увеличи­ваются, а между продольными — уменьшаются.

Описанный опыт можно рассматривать как подтверждение гипотезы плоских сечений; при этом предполагают, что внутри бруса деформации имеют тот же характер, что и на его поверхности.

Представим себе, что брус состоит из бесконечно большого числа продольных элементов, имеющих бесконечно малые («точечные») поперечные сечения. Эти элементы здесь и в даль­нейшем будем условно называть волокнами.

Из гипотезы Бернулли следует, что все волокна в рассма­триваемом случае деформируются одинаково. При однород­ном материале равным деформациям соответствуют одина­ковые напряжения. Таким образом, приходим к заключению, что при растяжении (сжатии) бруса нормальные напряжения рас­пределены по его поперечному сечению равномерно. Подчеркнем, что распределение напряжений не зависит от формы поперечного сечения.

Для определения нормальных напряжений используем вы­ражение 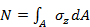. Вынося σ_z (постоянная величина!) за знак интеграла, получаем:

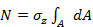.= σ_zA,

где А – площадь поперечного сечения бруса.

Для нормальных напряжений принимают то же правило знаков, что и для продольных сил, т. е. при растяжении считают напряжения положи­тельными.

Фактически распределение напряжений в сечениях бруса, примыкающих к месту приложения внешних сил, зависит от способа приложения нагрузки и может быть неравномерным. Экспериментальные и теоретические исследования показывают, что это нарушение равномерности распределения напряжений носит местный характер. В сечениях бруса, отстоящих от ме­ста нагружения на расстоянии, примерно равном наибольшему из поперечных размеров бруса, распределение напряжений можно считать практически равномерным.

Рассмотренное положение является частным случаем принципа Сен-Венана, который можно сформулировать следующим образом: распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения.

В частях, достаточно удаленных от места приложения сил, распределение напряжений практически зависит только от стати­ческого эквивалента этих сил, а не от способа их приложения.

Таким образом, применяя принцип Сен-Венана и отвлекаясь от вопроса о местных напряжениях, имеем возможность (как в этой, так и в последующих лекциях курса) не интересоваться конкретными способами приложения внешних сил. В местах резкого изменения формы и размеров поперечного сечения бруса также возникают местные напряжения. Это явле­ние называют концентрацией напряжений, которую в этой лекции учитывать не будем.

В тех случаях, когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно по­казывать закон их изменения по длине бруса в виде графи­ка - эпюры нормальных напряжений.