Меры центральной тенденции
Лекции по математическим методам в психологии
· Проблемы измерения в психологии и виды шкал
· Типы данных
· Правила ранжирования
· Меры центральной тенденции
· Меры изменчивости
· Нормальное распределение
· Асимметрия и эксцесс. Проверка нормальности распределения
· Формулы приближенных вычислений
· Методы первичного описания данных
· Алгоритм построения диаграммы
· Пример построения гистограммы
· Статистическая значимость
· Статистические гипотезы
· Зависимые и независимые выборки
· Степени свободы
· Классификация и назначение критериев
· Понятие корреляции
· Классификации коэффициентов корреляции
· Определение значимости корреляции
· Коэффициент линейной корреляции
· Уровень значимости корреляции
· Регрессионный анализ
· Вычисление ранговой корреляции по Спирмену
· Ранговая корреляция по Спирмену для связанных рангов
· Вычисление ранговой корреляции по Кендаллу
· Сравнение эмпирического и равномерного распределений
· Сравнение эмпирических распределений
· Поправка Йетса на непрерывность
· Вычисление сопряженности для номинативных переменных
· T-критерий для несвязанных (независимых) измерений
· U-критерий Манна-Уитни
· T-критерий для связанных (зависимых) измерений
· Т-критерий Вилкоксона (ранговый критерий для повторных измерений)
· Общие принципы дисперсионного анализа
· Однофакторный дисперсионный анализ
· Двухфакторный дисперсионный анализ
· Корреляционный анализ
· Факторный анализ
· Кластерный анализ
Проблемы измерения в психологии и виды шкал
Измерение – это приписывание числовых форм объектам. Выделяют 4 типа измерительных шкал.
1. Номинативная (номинальная, категориальные)
2. Порядковая (ранговая, ординальная)
3. Интервальная
4. Шкала отношений
Последние два вида шкал называют также метрическими шкалами.
Номинативная шкала – это шкала, в которой не выражены количественные характеристики объектов. Учитывается только то свойство объектов, что они разные. Эта шкала используется для классификации объектов. Например:
| Испытуемый | Выполнение тестового задания |
| Кор-ев | Выполнил |
| Пан-ев | Выполнил |
| Ер-в | Не выполнил |
| Вас-ев | Выполнил |
| Арт-ев | Не выполнил |
| Мих-ов | Выполнил |
Таким образом, людей по критерию выполнения-невыполнения задания можно отнести к одному из двух разрядов. Разрядов в номинативной шкале может быть и больше.
Порядковая (ранговая) шкала позволяет ранжировать объекты (присваивать им ранги) по какому-либо признаку. Например:
| Очередность решения задания | Испытуемый |
| Кор-ев | |
| Пан-ев | |
| Вас-ев | |
| Мих-ов |
При построении порядковой шкалы учитывается, что одно из чисел больше или меньше другого (производится ранжирование). Но при этом нельзя сказать, насколько оно больше или меньше.
Интервальная шкала – это шкала, классифицирующая по принципу «больше (меньше) на определенное количество единиц». Например:
| Время решения задания | Испытуемый |
| Произвольная точка отсчета | Кор-ев |
| На 7 сек дольше Кор-ва | Пан-ев |
| На 10 сек дольше Кор-ва | Вас-ев |
| На 15 сек дольше Кор-ва | Мих-ов |
То есть, по этой шкале уже можно количественно зафиксировать степень выраженности.
На этой шкале может быть нулевая отметка, но выбранная произвольно. Так, на температурной шкале Цельсия (интервальная шкала) за 0° выбрана температура таяния воды при давлении в 1 атм.
Абсолютная шкала (шкала отношений) - шкала, классифицирующая по принципу «больше (меньше) в определенное количество раз.
| Кор-в | Пан-в | Вас-в | Мих-в |
Из этой шкалы видно, что Кор-в выполнил задание в 2 раза медленнее Мих-ва и в 0,6 раз медленнее Вас-ва. Эта шкала отличается от предыдущей тем, что предполагает наличие абсолютного нуля. Например, у температурной шкалы по Кельвину (шкала отношений) за 0° выбрана точка, когда любое тепловое движение молекул прекращается.
Интервальную и абсолютную шкалы также принято называть метрическими шкалами.
Типы данных
Данные – это основные элементы, подлежащие классифицированию или разбитые на категории с целью обработки. Выделяют три типа данных:
1. Метрические данные: количественные данные, получаемые при измерениях. Их можно распределить на шкале интервалов или отношений.
2. Ранговые данные, соответствующие местам этих элементов в последовательности, полученной при их расположении в возрастающем порядке. Эти данные можно представить в виде порядковой шкалы.
3. Номинативные данные: категориальные (качественные) данные, представляющие собой особые свойства элементов выборки. Например, цвет глаз у испытуемых. Эти данные нельзя измерить, но можно оценить их частоту встречаемости.
Правила ранжирования
Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Таким образом, метрические значения переводятся в ранговые. При этом фиксируются различия в степени выраженности свойств. В процессе ранжирования следует придерживаться 2 правил.
Правило порядка ранжирования. Надо решить, кто получает первый ранг: объект с самой большей степенью выраженности какого-либо качества или наоборот. Чаще всего это абсолютно безразлично и не отражается на конечном результате. Традиционно принято первый ранг приписывать объектам с большей степенью выраженности качества (большему значению – меньший ранг). Например, чемпиону присуждают первое место, а не наоборот. Хотя, и здесь, если бы был принят обратный порядок, то результаты не изменились бы. Так что порядок ранжирования каждый исследователь вправе определять сам. Например, Е.В. Сидоренко рекомендует меньшему значению приписывать меньший ранг. В некоторых случаях это удобнее, но непривычнее.
Например: имеется неупорядоченная выборка, данные которой необходимо проранжировать. {2, 7, 6, 8, 11, 15, 9}. После упорядочивания выборки ранжируем ее.
| Метрические данные | Ранги | Альтернативный вариант: | Метрические данные | Ранги |
Отдельно следует сказать следующее. Существует группа редко используемых непараметрических критериев (Т-критерий Вилкоксона, U-критерий Манна-Уитни, Q-критерий Розенбаума и др.), при работе с которыми всегда надо меньшему значению приписывать меньший ранг.
Правило связанных рангов. Объектам с одинаковой выраженностью свойств приписывается один и тот же ранг. Этот ранг представляет собой среднее значение тех рангов, которые они получили бы, если бы не были равны. Например, надо проранжировать выборку, содержащую ряд одинаковых метрических данных: {4, 5, 9, 2, 6, 5, 9, 7, 5, 12}. После упорядочивания выборки следует вычислить среднее арифметическое значение связанных рангов.
| Метрические данные | Предварительное ранжирование | Окончательное ранжирование |
| (2+3)/2=2,5 | ||
| (2+3)/2=2,5 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
Меры центральной тенденции
Существуют 3 способа выражения центральной тенденции распределения: мода, среднее арифметическое, медиана.
Мода – это наиболее часто встречающееся значение в ряду данных. Например, в следующей выборке: {2, 3, 5, 1, 4, 5, 6, 5, 2} модой будет являться значение 5 (обозначатся следующим образом: Мо = 5). Если массив содержит 2 моды, то распределение называется бимодальным. Таким примером может служить выборка {3, 3, 5, 1, 4, 5, 6, 5, 3}. Здесь Мо1 = 5, а Мо2 = 3.
Бимодальное или полимодальное распределение могут рассматриваться как признак неоднородности выборки. Например, школьный класс образован в результате механического слияния двух разных классов, и показатели мод интеллекта были изначально различны. После слияния в объединенной выборке профиль интеллекта будет иметь 2 моды.
Среднее арифметическое – это отношение суммы всех значений данных к числу слагаемых. Среднее арифметическое обозначается как Мх или М. Число слагаемых (то есть объем выборки) обозначается буквой n.
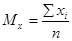
В качестве примера можно рассмотреть последний массив:
{8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20}.
Мх = (8 + 9 + 11 + 2 * 12 + 13 + 14 + 17 + 2 * 19 + 2 * 20) / 12 = 14,5
Если в ряду данных присутствуют числа со знаком «минус», то суммирование производится с учетом этих знаков.
Медиана разбивает выборку на 2 равные части. Для определения медианы рекомендуется сначала упорядочить данные. Например, для определения значения медианы в массиве {8, 11, 12, 20, 12, 13, 9, 15, 19, 17, 19} необходимо этот массив упорядочить (произвести сортировку по возрастанию): {8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20}. Медиана будет равна 13 (обозначатся след. образом: Ме = 13). Если количество данных в выборке четное, то медиана равна средней арифметической между двумя центральными значениями. Например, если добавить в последнюю выборку значение 20, и упорядоченный массив примет следующий вид: {8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20, 20}, то медиана будет равна 14. В подобном случае медиана не может соответствовать ни одному из значений выборки. Медиана может принимать и дробные значения. Например, если мы в последнем примере 15 (одно из двух центральных значений) заменим на 14, то выборка примет вид {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20} и медиана будет равна 13,5.
Меры изменчивости
В качестве наиболее часто используемых мер изменчивости следует назвать размах, дисперсию, стандартное отклонение.
Размах – это разница между максимальным и минимальным значениями.
Р = Хmax – Xmin
Для определения размаха выборку необходимо сначала уорядочить. Например, в массиве данных {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20} размах будет равен разности между наибольшим и наименьшим значениями, то есть 20 – 8 = 12. но если бы выборка была неупорядочена и имеет большой объем, было бы трудно найти минимальное и максимальное значения.
Дисперсия – это мера разброса данных относительно среднего значения.
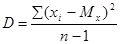
Если вычисление дисперсии производится вручную, то рекомендуется пользоваться специальной таблицей. Например, необходимо вычислить дисперсию для следующего массива данных {5, 2, 5, 3, 4, 3, 4, 3, 3, 1, 2, 1}. Упорядоченные данные заносятся в таблицу.
| Хi | Мx | Хi - Мx | (Хi – Мx)2 |
| -2 | |||
| -2 | |||
| -1 | |||
| -1 | |||
| n = 12, Мx = 3 | Σ(Хi – Мx)2 = 20 |
В соответствии с формулой D = 20 / (12 – 1) = 1,818
Стандартное отклонение представляет собой квадратный корень из дисперсии:
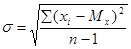
По ряду причин этот показатель является более удобным, чем дисперсия.
