Построение и решение линейных оптимизационных моделей
Условие
При выполнении ремонтов локомотивов расходуются трудовые ресурсы, станко-часы и горюче-смазочные материалы (ГСМ). Месячный фонд рабочего времени ремонтных рабочих составляет 600 чел.-ч., фонд рабочего времени оборудования – 240 станко-часов, а месячный запас горюче-смазочных материалов составляет 200 т. Расходы ресурсов на выполнение одного ремонта определенного вида заданы в таблице.
| Вид ресурсов | Расход ресурсов на выполнение 1 ремонта | Запасы (нормы расхода) ресурсов | ||
| КР* | ТР1** | ТР2*** | ||
| Трудовые ресурсы | 0,7 | 0,4 | 0,5 | |
| Станко-часы | 0,3 | 0,2 | 0,4 | |
| ГСМ | 0,5 | 0,3 | 0,3 |
Составить оптимальную программу ремонтов, чтобы суммарная прибыль локомотивного депо была максимальной, если известно, что прибыль от выполнения одного капитального ремонта (КР) составляет 130 тыс. руб., одного ТР1 – 150 тыс. руб. и одного ТР2 – 140 тыс. руб.
Математическая модель
Используя уже готовую дескриптивную модель, содержащую переменные и ограничения модели (задача 1 п.1)
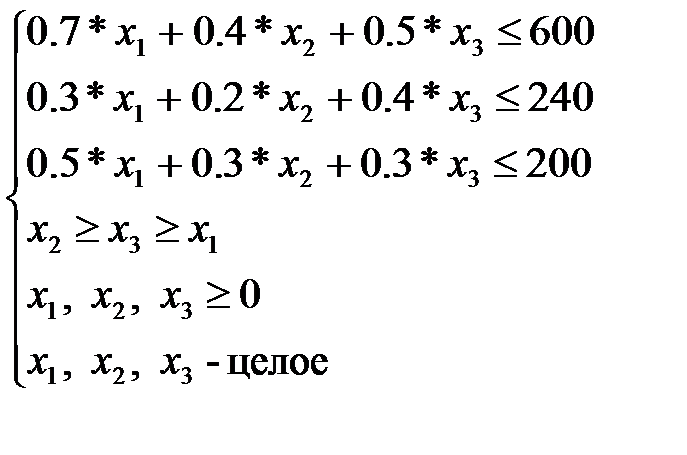
где: x1 – кол-во капитальных ремонтов;
x2 – кол-во 1-ых текущих ремонтов ;
x3 – кол-во 2-ых текущих ремонтов.
Целевая функция F= 130x1 + 150x2 +140х3 –> mах (необходимо максимизировать прибыль локомотивного депо)
Целевая функция является критерием выбора наилучшего значения переменных модели.
Результаты решения задачи с помощью MS Excel«Поиск решение»
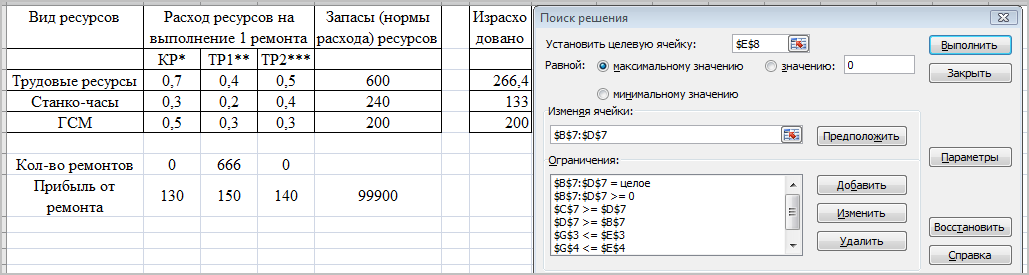
При оптимальных значениях переменных х1=0, х2=666, х3=0, целевая функция F достигает максимального значения и равна F=99900 тыс.руб.
Вывод
Поскольку система уравнений, описывающая условия дескриптивной модели, имеет дополнительные ограничения и содержит целевую функцию то найденные значения переменных, являются оптимальным решением данной системы.
Решение Ттранспортной задачи линеного програмирования в матричной постановке методом потенциалов
Условие
| Ai= | |||||
| Bj= | |||||
| Cij= | |||||
Суммарный объем производства всех поставщиков ∑Аi= 657
Суммарный объем спроса все потребителей ∑Bj = 454
Суммарный объем производства поставщиков превышает объемы спроса потребителей (∑Аi >∑Bj), следовательно, это задача открытого типа.
Приведем задачу к закрытому типу. Для этого введем фиктивного потребителя Вф с объемом спроса равным В5=∑Аi-∑Bj =657-454=203 и стоимостью перевозок = 0
Оптимальный план F=∑∑Cij*Xij - должен быть минимальным.
| Спрос | ||||||
| Поставки | В1 | В2 | В3 | В4 | В5 | |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| А4 | ||||||
| А5 |
Первоначальный план строим методом северо-западного угла
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| - | 102 | + | |||||||||||
| А2 | U2= | ||||||||||||
| + | - | ||||||||||||
| А3 | U3= | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
Нашли начальное решение, т.е. израсходовали все запасы поставщиков и удовлетворили все потребности потребителей: F0 = 3847
Далее для всех свободных клеток найдем положительные сдвижки =Vi-Cij-Uj. Пока есть положительные сдвижки >0, План не оптимален. Выбираем максимальную сдвижку. С нее начнем строить новый план. Для нового плана рассчитаем потенциалы и сдвижки. Эти шаги повторяем до тех пор, пока будут положительные сдвижки >0
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| - | + | ||||||||||||
| А2 | U2= | ||||||||||||
| + | - | ||||||||||||
| А3 | U3= | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F1=3077
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| А2 | U2= | ||||||||||||
| - | 1 | + | |||||||||||
| А3 | U3= | ||||||||||||
| + | - | ||||||||||||
| А4 | U4= | ||||||||||||
| + | - | ||||||||||||
| А5 | U5= | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F2=2597
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| - | + | ||||||||||||
| А2 | U2= | ||||||||||||
| А3 | U3= | ||||||||||||
| + | - | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F3=2587
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| А2 | U2= | ||||||||||||
| А3 | U3= | ||||||||||||
| А4 | U4= | ||||||||||||
| - | + | ||||||||||||
| А5 | U5= | ||||||||||||
| + | - | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F4=1750
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| - | 32 | + | |||||||||||
| А2 | U2= | ||||||||||||
| А3 | U3= | ||||||||||||
| + | - | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| + | - | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F5=1394
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| - | + | ||||||||||||
| А2 | U2= | ||||||||||||
| А3 | U3= | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| + | - | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F6=1290
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | U1= | ||||||||||||
| А2 | U2= | ||||||||||||
| А3 | U3= | ||||||||||||
| А4 | U4= | ||||||||||||
| А5 | U5= | ||||||||||||
| V | V1= | V2= | V3= | V4= | V5= |
F7=1214
Для всех свободных клеток положительные сдвижки ≤0.
Получили оптимальный план перевозок.
Минимальная величина суммарных затрат = 1214
Оптимальный план перевозок, рассчитанный средствами Excel
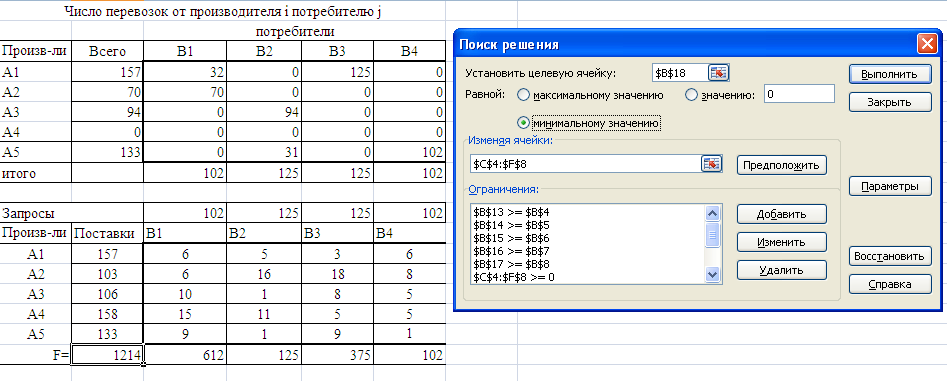
Вывод
Для одних и тех же исходных данных может быть несколько решений (оптимальных планов) с одинаковыми минимальными суммарными затратами. Это видно из решений методом потенциалов и средствами Excel.
При оптимальном плане перевозок стоимость величины суммарных затрат минимальна.
