Расчет реакторов с использованием математических моделей

Реактор идеального смешения

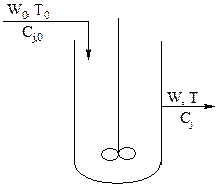
Идеальное перемешивание предполагает мгновенное усреднение концентраций всех веществ (включая входящих с потоком) и температуры по всему рабочему объему. Мгновенным можно считать перемешивание, когда время смешения много меньше времени пребывания в реакторе. Следствие: концентрация всех веществ и температура одинаковы в любой точке рабочего объема реактора.

Расчетное уравнение можно получить, составив материальный баланс для аппарата по веществу j (стационарный режим):

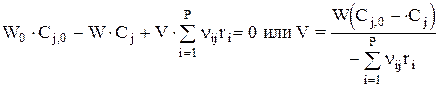или

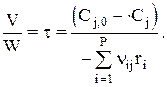Здесь n_ij берется с минусом для реагентов и с плюсом для продуктов; t — это среднее время пребывания (контакта). Здесь Р —число стадий, на которых участвует вещество j.

Из уравнения РИС можно найти рабочий объем V, используя, например, данные о степени превращения ключевого реагента А. Тепловой баланс РИС составляется для того, чтобы определить требуемую поверхность теплопередачи S_T.

Для систем, когда С_pj=const и DC_pj»0, можно записать уравнение теплового баланса (без учета тепла физических процессов и теплопотерь):

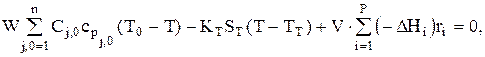где

К_Т — коэффициент теплопередачи; -DH_i — тепловой эффект i-й стадии, здесь Р — общее число стадий процесса.

Для простых реакций в качестве переменной удобно использовать Х_А при составлении материального и теплового балансов РИС.

Материальный баланс имеет вид:

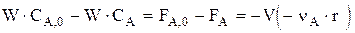или F_A,0×X_A=V×r_A, откуда

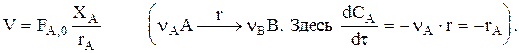
Тепловой баланс:

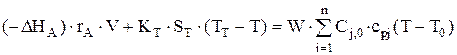или

.

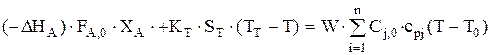Таким образом V определяется из уравнения материального баланса по А. Из уравнения теплового баланса определяют S_T. Концентрации ключевых веществ на выходе из реактора определяются из соответствующих уравнений материального баланса РИС. Это позволяет определить состав реакционной смеси, что необходимо для дальнейшего расчета аппаратов охлаждения и разделения этой реакционной смеси.

Методика расчета РИС

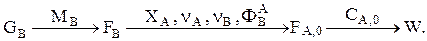
Дано G_B. Определяем 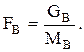Используя уравнение стехиометрического материального баланса, находим 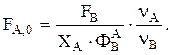Интегральную селективность Ф_В^А при Т=const можно, например, найти экспериментально. Затем находим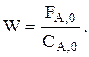

Зная W и F_А,0, определим V и S_T, а также концентрации всех ключевых веществ (если это нужно) в потоке на выходе из РИС. Выбираем 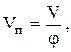при этом поверхность теплопередачи должна быть в реакторе не менее, чем рассчитанная S_T.

В реакторе создается такой гидродинамический режим (в рабочем объеме и в рубашке), чтобы К_Т было не меньше, чем принятое в расчетах.

Примеры. стр. 59-60.

Пример.

РИС

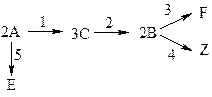
Представить материальный баланс для всех веществ.

W(CA,0—CA)=(—V)×(—2)(r1+r5) W(—CC)=(—V)×(3r1—3r2) W(—CB)=(—V)×(2r2—2r3—2r4) W(—CE)=(—V)×r5 W(—CF)=(—V)×r3 W(—CZ)=(—V)×r4

(1) (2) (3) (4) (5) (6)

Периодический реактор

В аппарат периодического действия за время осуществления собственно химической реакции t не вводят в него и из него не выводят материальные потоки. В периодических условиях практически всегда перерабатывают системы с неменяющимся объемом.

Теперь кинетическую характеристику процесса t можно получить, решая соответствующее уравнение для периодически работающего реактора: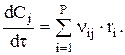

Для простой (одностадийной) реакции расходование основного реагента А во времени происходит по уравнению:

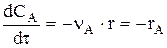или 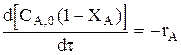откуда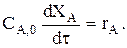

По этим уравнениям нахождение t возможно только в изотермических условиях.

В других случаях надо иметь еще уравнение теплового баланса, которое запишется так (считать Dс_р»0):

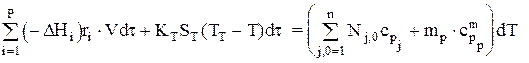или после преобразований:

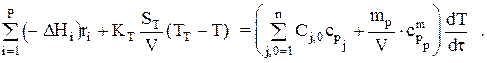
Здесь m_p — масса реактора; 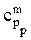— массовая теплоемкость материала реактора.

Тепловой баланс для простой реакции имеет вид:

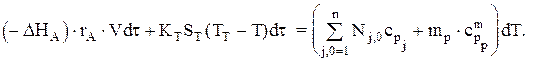
Зная, что C_A,0dX_A=r_A×dt, можно записать:

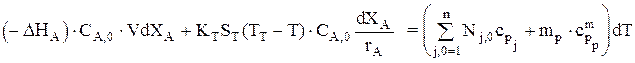или

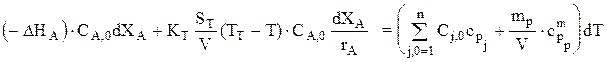
или

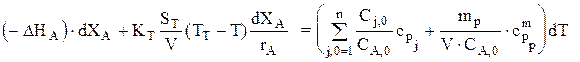
или

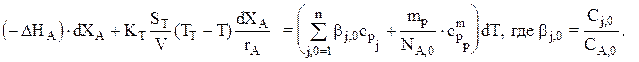
В общем случае для адиабатического режима имеем:

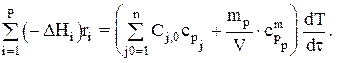
Для простой реакции при адиабатическом режиме имеем:

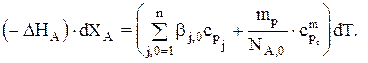
Если c_pj=const, то: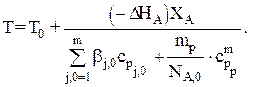

Решая совместно уравнения материального и теплового баланса определяют t и, соответственно, t_ц. Это позволяет для выбранного V найти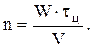

Методика расчета

Выбираем стандартный аппарат периодического действия V_п. Зная j, определяем V=V_п×j. Этот аппарат имеет некоторую фиксированную поверхность теплопередачи S_T. Выбрав расход теплоносителя G_T и число оборотов мешалки, т.е., зная гидродинамический режим движения реакционной массы и теплоносителя, определяем коэффициенты теплоотдачи a₁ и a₂, а затем и К_Т.

Решаем совместно уравнения материального и теплового баланса. Находим t и n ключевых веществ. Зная С_А и С_В, находим 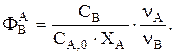Рассчитываем

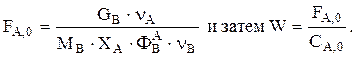
Теперь можно определить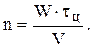

Примеры. Учебник, стр. 62-64

Реактор идеального вытеснения (РИВ)

Рассмотрим профиль линейных скоростей потока по радиусу трубки для режимов: 1) идеального вытеснения; 2) ламинарного; 3) турбулентного.

Cj(R)=const; T(R)=const;
РИВ	ламинарный поток	турбулентный поток

Наиболее близок к РИВ профиль скоростей турбулентного режима.

Условия применения модели РИВ:

1) нужен турбулентный режим движения потока в трубке;

2) отношение L/d несколько десятков(здесь d — диаметр трубки).

Окончательно применимость той или иной модели определяется на «холодных» (стендовых) установках при использовании метода трассёра (о чем речь пойдет позже).

Вывод расчетного уравнения РИВ (стационарный режим)

Составим материальный баланс для выделенного элементарного объема dV=S×dl, где S — сечение аппарата (трубки), l — переменная длина. Для вещества j при стационарном режиме имеем:

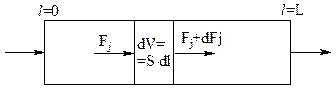
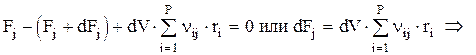
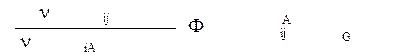Если w=const, то

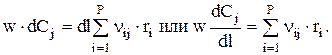Можно записать

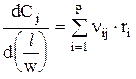или 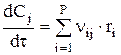, где t=l/w — это не астрономическое время, как в уравнении периодического реактора (его хронометром не измеришь), а время контакта (пребывания).

В случае простой реакции расчетное уравнение для РИВ удобно записывать, используя Х_А:

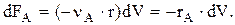
Учитывая, что F_A=F_A,0(1—X_A), получим

—F_A,0×dX_A=—r_A×dV Þ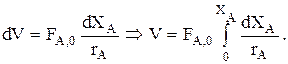

Тепловой баланс для РИВ в общем случае запишется так:

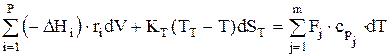или

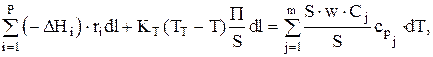где

П — периметр цилиндрической трубки (p×d);

S — сечение трубки (p×d²/4);

S_T — поверхность теплопередачи (dS_T=P×dl).

Теперь имеем:

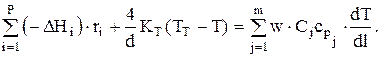
Если Т_Т меняется по длине реактора, то составляется уравнение теплового баланса для теплоносителя. При этом нужно знать температуру теплоносителя на входе в аппарат и его расход G_T. Температура теплоносителя на выходе из аппарата определяется при расчете.

Можно записать

G_T×c^m_pTdT_T=K_T(T—T_T)Pdl.

Возможен прямоток или противоток, что учитывается знаком в левой части уравнения.

Для простой реакции уравнение теплового баланса РИВ имеет вид:

.

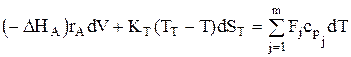Учитывая, что 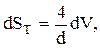запишем:

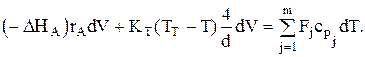
Для РИВ имеем:

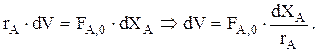
Тогда

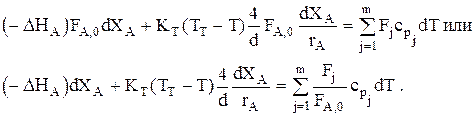Обозначим 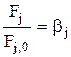. Тогда:

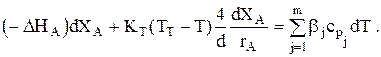
Для адиабаты, если считать c_pj,0=const и Dc_p»0, можно записать:

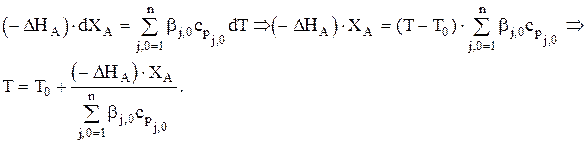
Это уравнение отличается от того, что получено для периодического реактора только на слагаемое в знаменателе, отвечающее за нагрев аппарата.

Методика расчета

1) простая реакция, т.е. Ф_В^А=1.

Задано G_В. Рассчитывают F_A,0 и w по схеме:

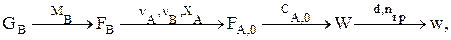где n_тр — число параллельных трубок в реакторе. w выбирают таким, чтобы режим в трубках был турбулентным. Конструируют аппарат из n_тр с диаметром d каждая. В межтрубное сечение подают теплоноситель с расходом G_Т. Рассчитывают a₁ и a₂, а затем и К_Т.

Решают совместно уравнения материального и теплового балансов и определяют L. Если L/d большое, то можно считать, что модель ИВ применима для расчета. Правильнее проверить применимость модели, используя метод трассера.

2) сложная реакция, т.е. Ф_В^А¹1.

Задаемся Ф_В^А, d, и n_тр. Тогда

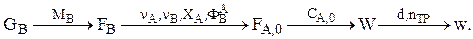
Режим в трубках должен быть турбулентным.

Рассчитываем К_Т. Решаем уравнения материального и теплового балансов. Находим L и концентрации ключевых веществ. Зная С_В и С_А, рассчитываем

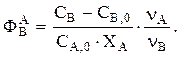
Расчет проводят до тех пор, пока выбранное и рассчитанное значения селективности не совпадут с заданной точностью. При этом необходимо, чтобы L/d равнялось нескольким десяткам.

Для реакции А ® В + (—DН) изменение температуры Т по длине аппарата l в РИВ будет иметь следующий вид:

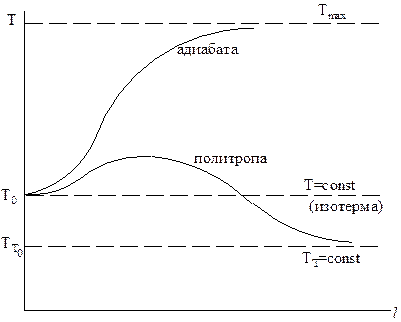
Профиль Т по l можно изменять, варьируя Т₀, Т_Т0, К_Т, G_T, S_T и т.д.

Примеры. Учебник, стр. 50-55.

Метод трассера

Строят физическую модель реактора («холодную модель»), отражающую его основные свойства. Например, строят одну трубку многотрубного реакторав натуральную величину. В нее подают поток с различной линейной скоростью. В поток вводять, например, импульсно некоторое вещество, концентрацию которого легко анализировать. Это вещество называется трассером. Обозначим через С=С/С₀ безразмерную концентрацию трассера и q=t/ 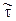— безразмерное время. Здесь 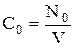, где N₀ — количество трассера, введенного в «холодную» модель с рабочим объемом V; С — текущая концентрация трассера; 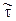— среднее время пребывания элементов потока в «холодной» модели; t — текущее время.

Кривые распределения С от q для различных моделей

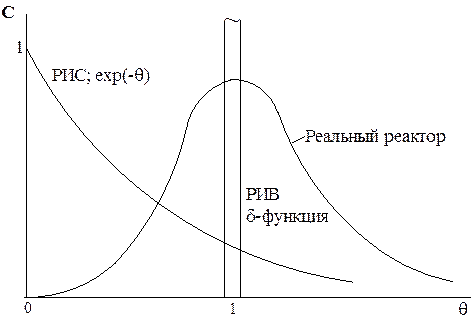
Расчет 1-го и 2-го моментов распределения:

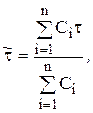где 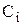— концентрация трассера в i-й пробе потока, выходящего из «холодной» модели; t — время отбора пробы.

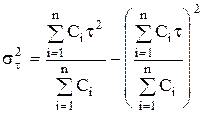и

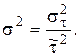
Диффузионная однопараметрическая модель

В гомогенных системах при небольших L/d, приходится учитывать в математической модели возможное осевое (обратное, продольное) перемешивание, которое характеризуется коэффициентом продольного перемешивания D_L. При этом считается, как и в модели РИВ, что по радиусу нет градиентов концентраций и температур.

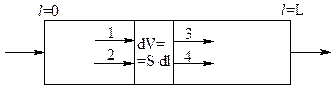
1,3 — конвективные потоки;

2,4 — диффузионные потоки.

Составим материальный баланс для элементарного объема dV, учитывая, что в отличие от РИВ, в выделенный объем вещество j вносится не только конвективным потоком, но и диффузионным (за счет обратного перемешивания). Считается, что перенос вещества за счет обратного перемешивания происходит по закону, аналогичному закону Фика.

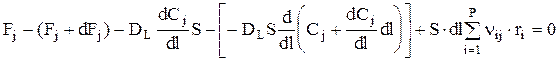	поток 1	поток 3	поток 2	поток 4

Откуда

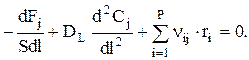Зная, что F_j=S×w×C_j, имеем:

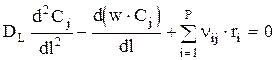или при w=const:

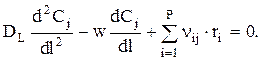
Граничные условия:

при l=0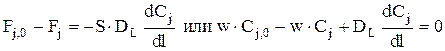

при l=L .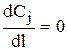

Введем следующие обозначения:

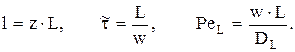
Тогда:

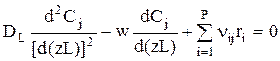
Далее

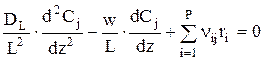или

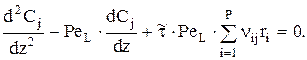
Запишем граничные условия так:

.

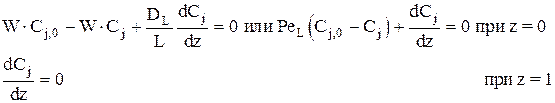Критерий Пекле находится при использовании «холодных» моделей по формуле: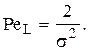

Тепловой баланс

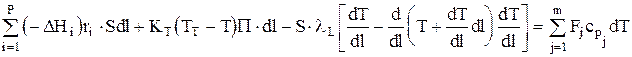
или после преобразований имеем:

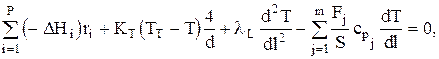где l_L — коэффициент теплопроводности реакционной смеси.

Заменим 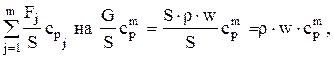где r —плотность реакционной массы, c_p^m — теплоемкость реакционной массы; G — массовый поток реакционной смеси.

Тогда:

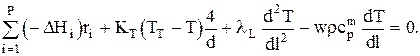
Граничные условия:

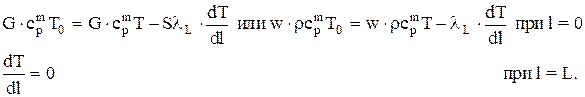
Известно, что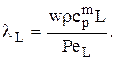

Тогда:

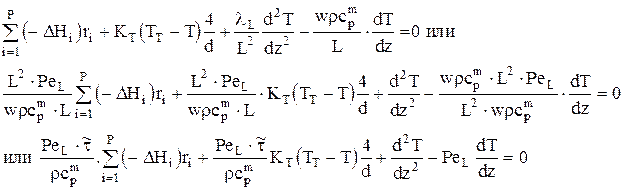
Граничные условия:

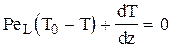	при z=0
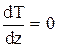	при z=1

Очевидно, что уравнения теплового и материального баланса можно решить, если известно значение Pe_L. Оказывается, что для технических расчетов справедливо соотношение 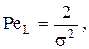Pe_L определяется экспериментально на «холодной» модели.

Методика расчета.

Как и для РИВ задаемся Ф_В^А, находим w для выбранных d и n_тр.. Задаемся расходом G_T и рассчитываем a₁, a₂ и затем К_Т.

Выбираем некоторую длину трубки L. Для значений w и L на «холодной» модели определяем Ре_L. Знаем, что L/w= 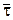. Решаем уравнения материального и теплового балансов с непрерывной коррекцией значений Ф_В^А и L.

Пример. Учебник, стр. 69-70.

Ячеечная модель

Модель потока с осевым перемешиванием можно представить как ряда РИС, соединенных последовательно (каскад РИС).

Число реакторов в ячеечной модели определяют из соотношения: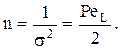

Теперь имеем:

Введем обозначения:

V=V_общ/n — объем одной ячейки идеального смешения;

V_общ — общий объем реактора;

n — число ячеек.

Для реактора цилиндрической формы можно записать:

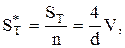где S_T* — поверхность теплопередачи одной ячейки,

S_T — общая поверхность теплопередачи в реакторе.

Составим материальный баланс по веществу j для каждой ячейки идеального смешения:

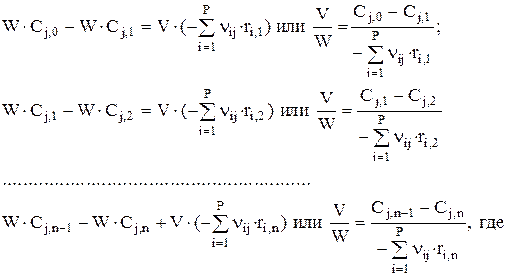
C_j,1; C_j,2; ... C_j,n — концентрация вещества j в 1, 2, ... n ячейке идеального смешения;

r_i,1; r_i,2; ... r_j,n — скорость i-й реакции в 1, 2, ... n ячейке идеального смешения.

При составлении материального баланса по основному реагенту А, для которого задана конечная степень превращения или, что точнее, С_А,n, имеем систему n алгебраических уравнений. В ней неизвестными являются С_А,1, С_А,2, ... С_А,n—1, и V.

Эта система из n уравнений, если имеется теплообмен через стенку, может быть решена только совместно с системой уравнений теплового баланса для ячеек идеального смешения. Тепловой баланс имеет вид, считая c_pj=const и Dc_pj»0:

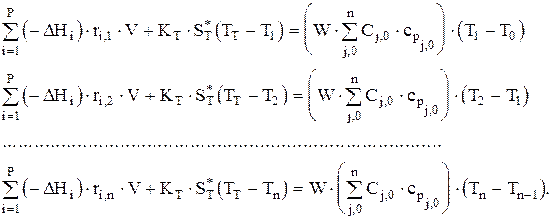
В этой системе уравнений неизвестными являются Т₁, Т₂, .... Т_n температур. Совместное решение систем уравнений материального и теплового балансов позволяет определить, например, V, n-1 концентрацию основного реагента и n температур в ячейках идеального смешения.

Пример.

Дана реакция 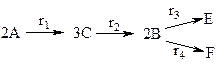. Составить уравнение материального баланса для ячеечной модели, если r_i=exp(a_i-b_i/T)C_j. Число ячеек n; i=1, 2, 3, 4; j=A, B, C, E, F.

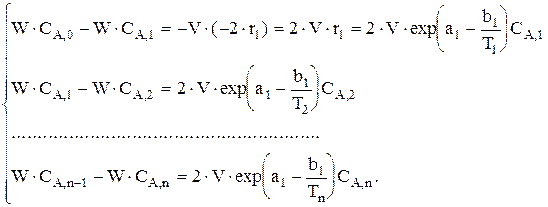
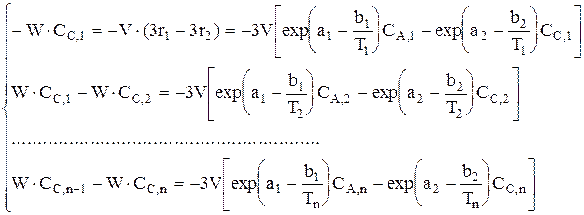
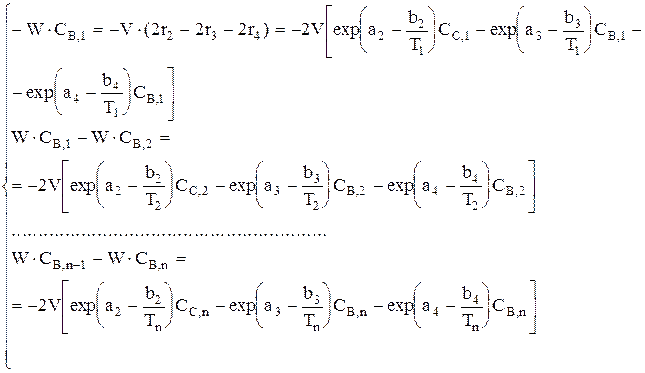Аналогично материальный баланс записывается для Е и F.

Методика расчета

На «холодной» модели находим s² для различных линейных скоростей потока и L.

Выбираем некоторый аппарат с диаметром трубки d и числом параллельно работающих трубок n_тр. Зная s², определим число ячеек. Зная G_В, и задавшись Ф_В^А, определяем W и w. Режим в трубках должен быть турбулентным. Если нужно, изменяем число трубок n. Задаемся расходом теплоносителя G_Т и рассчитываем a₁, a₂ и затем К_Т. Решаем совместно уравнения материального и теплового балансов. Находим С_В на выходе из аппарата, т.е. в n-ой ячейке. Рассчитываем 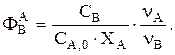Сравниваем полученные значения L и Ф_В^А с выбранными. Проводим коррекцию до совпадения выбранных и рассчитанных L и Ф_В^А с заданной точностью.

Реакторы для гетерогенных систем

Реакции газообразных веществ на поверхности твердых катализаторов широко распространены в технологии нашей специальности: крекинг, риформинг, синтезы на основе СО и Н₂ и др. Катализаторы могут находиться в стационарном, движущемся или псевдоожиженном состоянии. Это определяется кинетикой процесса, тепловым эффектом реакции, условиями теплообмена, продолжительностью работы катализатора без заметной потери активности.

Преимущества псевдоожиженного слоя: изотермичность, отсутствие диффузионных сопротивлений; возможность непрерывной регенерации катализатора.

Недостатки: невысокая удельная производительность; истирание катализатора (эрозия стенок аппарата); загрязнение катализаторной пылью «сырого» продукта реакции; сложность поддержания необходимой циркуляции катализатора.

Расчет реактора со стационарным слоем катализатора по квазигомогенной модели

Предполагается, что в выделенном элементарном объеме dV=dx×dy×dz температура потока и катализатора одинакова; изменением температуры в зерне катализатора можно пренебречь. Такие допущение справедливы при отсутствии сопротивлений массо- и теплопереносу от реакционной массы к поверхности катализатора и далее к его центру. Квазигомогенная модель рассматривает содержимое реактора как однородную непрерывную среду. В этом случае используются константы, отнесенные ко всему слою.

Слой зернистого катализатора чаще всего имеет низкую теплопроводность. При теплообмене через стенку это приводит к возникновению радиальных градиентов температур в цилиндрических трубках. При наличии в слое химических реакций температурные градиенты вызывают градиенты концентраций веществ. Составим материальный баланс по веществу j для выделенного элементарного объема слоя dV.

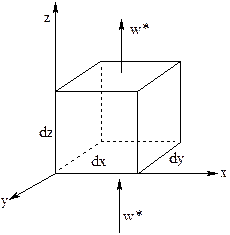
Конвективный поток подается снизу вверх по направлению координаты z. Он проходит через нижнюю и верхнюю элементарные поверхности dx×dy и, соответственно, равен:

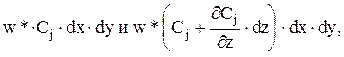где w* — фиктивная линейная скорость потока.

Через поверхности dx×dz и dy×dz конвективный поток не проходит (отсутствует).

Диффузионный поток через нижнюю и верхнюю элементарные поверхности dx×dy равен:

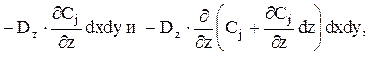где D_z — коэффициент перемешивания по оси z.

Аналогичные потоки существуют и через элементарные поверхности dx×dz и dy×dz. Тогда

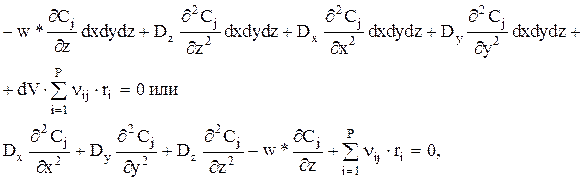
где r_i — скорость i-й стадии, на которой участвует вещество j, отнесенная к единице объема слоя [моль j/(м³×с)].

Для цилиндрической трубки с координатами l — переменная длина и R — переменный радиус можно записать:

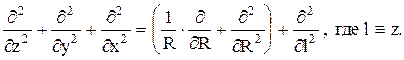
Тогда материальный баланс можно записать так:

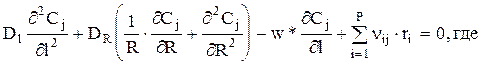D_l, D_R — коэффициенты перемешивания (диффузии) потока по длине и радиусу слоя.

Коэффициенты D_l, D_R, l_l, l_R определяются на «холодных» моделях для реальных физико-химических систем.

Аналогично уравнение теплового баланса в цилиндрических координатах будет иметь вид:

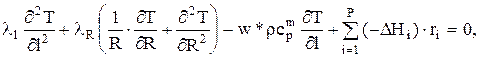
где l_l, l_R — эффективные коэффициенты теплопроводности по длине и радиусу слоя катализатора.

Решение дифференциальных уравнений материального и теплового балансов в частных производных возможно, если известны соответствующие граничные условия. Они таковы.

1) на входе в слой, т.е. при l=0

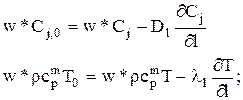
2) на выходе из слоя, т.е. при l=L

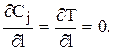
3) на оси слоя катализатора (в силу симметрии), т.е. при R=0

;

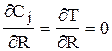4) на границе со стенкой, т.е. при R=R* ( где R* — расстояние от оси слоя до стенки цилиндрической трубки, т.е. ее радиус).

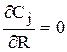
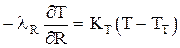(это поток тепла через стенку и далее по радиусу слоя) при R=R*

Если температура теплоносителя Т_Т меняется по длине реактора, то для режима идеального вытеснения теплоносителя имеем:

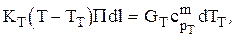где П — периметр трубки с катализатором, через поверхность которой осуществляется теплообмен..

Полученные уравнения с граничными условиями решают численными методами на ЭВМ.

Если слой высокий (L/d_ч>100, где d_ч — диаметр частицы катализатора), а диаметр трубки небольшой (градиентом С_j и Т по радиусу можно пренебречь), то перемешиванием по длине и радиусу можно пренебречь (модель РИВ).

В общем виде имеем двухпараметрическую диффузионную модель.

Псевдоожиженный слой

Начнем пропускать газ через стационарный слой мелких твердых частиц снизу вверх. Слой будет взвешенным, когда его сопротивление потоку станет равным его весу. При этом линейная скорость газа называетсят критической w_кр*. Дальнейшее увеличение скорости может привести к тому, что частицы в режиме пневмотранспорта будут уноситься из реактора. Линейную скорость при этом обозначают w_в (витание).

Свободный кипящий слой может существовать при условии w_кр*<w*< w_в*. Гидродинамическую обстановку кипящего слоя часто характеризуют числом псеводоожижения .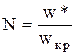

Считают, что весь избыток газа сверх соответствующего скорости w_кр проходит через слой в виде пузырей.

Таким образом газовый поток разбивается на две части (две фазы):

1) сплошной,

2) дискретный (пузыри).

Для дискретной фазы часто принимают режим идеального вытеснения, а для сплошной — идеального смешения. Состав реакционной смеси в обеих фазах изменяется также за счет газового обмена между ними. В дискретной фазе катализатора нет и, соответственно, не осуществляется химическая реакция. Запишем уравнения материального баланса для j-го вещества в обеих фазах.

Для дискретной 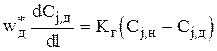, где w_д*= w*— w_кр (w_кр может быть рассчитано для каждого конкретного случая по эмпирическим уравнениям);

С_j,д и С_j,н концентрация вещества j в дискретной и непрерывной фазах;

l — переменная высота псевдоожиженного слоя;

К_г — коэффициент массообмена между дискретной и сплошной фазами, отнесенный к единице объема псевдоожиженного слоя.

Для непрерывной фазы

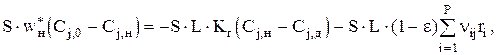
где

w_н*= w_кр;

S — сечение реактора;

L — высота псевдоожиженного слоя;

e — доля пузырей в объеме псевдоожиженного слоя;

С_j,₀ и С_j,н — концентрация вещества j во входящем в реактор потоке и внепрерывной фазе;

r_i — скорость i-й стадии химического процесса, на которой принимает участие j; отнесенная к единице объема слоя при w*=w_кр., т.е. когда в слое нет пузырей.

Развитой псевдоожиженный слой (w*>w_кр) характеризуется своей изотермичностью. Это достигается тем, что газовые пузыри приводят в интенсивное движение твердые частицы. Таким образом пузыри, создавая байпасный поток, уменьшают удельную производительность реактора, а с другой стороны — обеспечивают его изотермичность. Следовательно, при Т=const можно, решая уравнения материального баланса j-го вещества в обеих фазах, определить высоту псевдоожиженного слоя.

Методика решения

Осуществляют решение

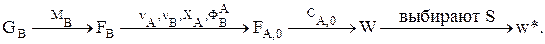Рассчитывают w_кр=w_н*. Находят w_д*=w*—w_кр.

Выбирают L. Решают совместно оба уравнения материального баланса с двумя неизвестными С_j,д и С_j,н. Находят С_j,д и С_j,н на выходе из реактора, т.е. при l=L.

Осуществляют проверку правильности выбора L.

Для основного реагента А известна степень превращения Х_А (или 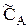на выходе из реактора).

Рассмотрим схематично процесс расходования А в псевдоожиженном слое.

Над слоем потоки непрерывной и дискретной фаз смешиваются, образуется суммарный выходной поток, в котором концентрация А известна. Запишем материальный баланс по А для зоны объединения потоков:

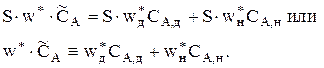
Если последнее уравнение справедливо (верно), т.е. соблюдается равенство, то L выбрано правильно.

Тепловой баланс составляют в целом для всего реактора (как для РИС), учитывая, что Т=const.

Из теплового баланса определяют S_T.

Камера периодического коксования.

Камеру коксования можно рассматривать как периодически работающий реактор, в котором нужно учитывать градиент температур по ширине камеры. Градиентом температур по ее длине и высоте можно пренебречь (вытягивают факел и используют несколько вертикалов).

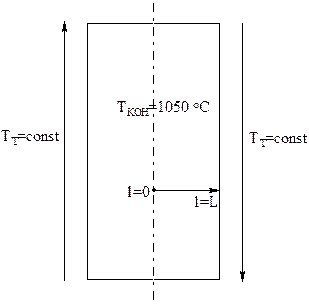Здесь L — это полуширина камеры. Для процесса образования кокса из шихты примем следующую кинетическую схему: 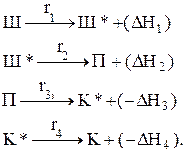Здесь Ш, Ш*, П, К*, К — это, соответственно, влажная шихта, сухая шихта, пластический слой, полукокс, кокс.

Каждая из стадий процесса описывается кинетическим уравнением первого порядка:

r_i=k_0i×exp(-E_i*/T)×C_j, где k_0i — предэкспоненциальный множитель i-ой стадии; E_i* — значение энергии активации i-ой стадии, деленное на R; C_j — концентрация j-го вещества.

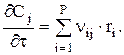
Материальный баланс будет иметь следующий вид:

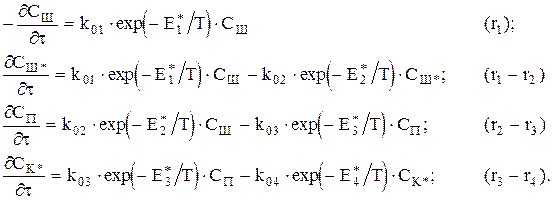
Начальные условия:

t=0, С_Ш=С_Ш,0= 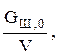где G_Ш,0 — масса шихты, загруженной в камеру коксования с рабочим объемом V.

Запишем уравнение теплового баланса:

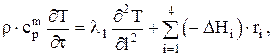где

l_l — коэффициент теплопроводности слоя;

r — средняя плотность реакционной массы в камере коксования;

с_р^m — ее средняя теплоемкость.

Начальные и граничные условия:

t=0, Т=Т₀ и

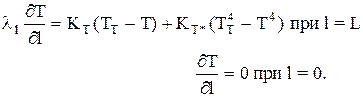
Здесь Т_Т — средняя температура дымовых газов в простенках;

К_Т и К_Т* — коэффициенты теплопередачи от дымовых газов к слою за счет конвекции и излучения.

Решают совместно уравнения материального и теплового балансов до момента t, когда на оси, т.е. при l=0, температура не станет равной 1000-1050 ^оС. Для каждого состава шихты эта температура имеет свое значение. Достижение этой температуры на оси камеры говорит об окончании процесса. Найденное значение t используют для расчета t_ц=t+t_нз. Затем уже по известной методике расчета периодических реакторов определяют число камер в батарее.

Математическая модель позволяет определить t для камер различной ширины, шихт различного состава, термоподготовленной шихты и т.д.