Безразмерные характеристики материального баланса

Пример

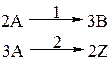Дано: СА,0, СВ,0 = СZ,0 = 0, СВ и СZ. Найти СА.

Решение.

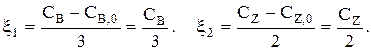
Теперь:

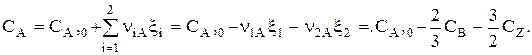
Запишем теперь скорость химической реакции для i-ой стадии:

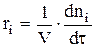, где t — текущее время.

Если V=const, то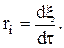

Скорость реакции по веществу j, участвующему на Р стадиях, запишется так:

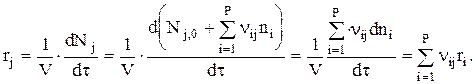
Необходимо отметить, что r_i всегда положительна. Знак r_i определяется знаком n_ij. Скорость r_i положительна для веществ, образующихся на i-ой стадии, и отрицательна для веществ расходующихся.

Если V=const, то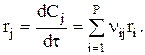

Пример

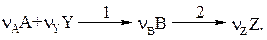Это двухстадийная реакция. Соответственно,

r₁ и r₂ –скорости 1 и 2 стадий. Считать (это дано), что по каждому реагенту (А, Y и В) реакция имеет первый (частный порядок); V=const.

Тогда: r₁ = k₁·C_AC_Y и r₂ = k₂·C_В. Здесь k₁ и k₂ –константы скоростей 1 и 2 стадий.

Найдем кинетическое описание процесса, т.е. изменение концентраций двух ключевых веществ, например, А и В. Очевидно, зная концентрации А и В в любой момент времени, можно найти концентрации Y и Z в этот же момент времени, используя стехиометрические соотношения материального баланса.

Решение.

Запишем r_A=—n_Ar₁ и r_В=n_Вr₁—n_Вr₂.

Тогда

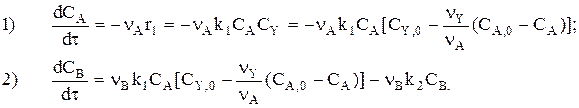
Система «1-2» решается совместно, и для любого t находим С_А и С_В. Затем находят 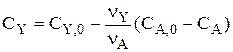и

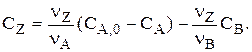
Пример.

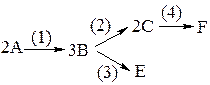
Требуется написать кинетическую схему.

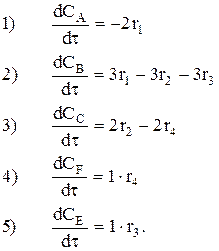
Безразмерные характеристики материального баланса

Введем понятие основного реагента. Это реагент, который взят в недостатке, т.е. тот, у которого отношение начального количества вещества к положительному значению его стехиометрического коэффициента будет наименьшим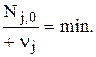

Степень превращения основного реагента А – это доля израсходованного реагента А, пошедшего на образование всех веществ:

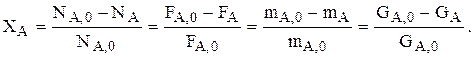Если V=const, то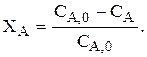

Степень превращения может меняться от 0 до 1 или от 0 до 100 %. Очевидно, что N_A=N_A,0–N_A,0×X_A=N_A,0×(1–X_A) и, если V=const, то С_A=С_A,0×(1–X_A).

Для простой реакции N_A,0–N_A=n_А×h и N_A,0–N_A=N_A,0×X_A, т.е. n_А×h= N_A,0×X_A и 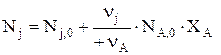Здесь n_А положительно, а n_j имеет знак минус (–) для веществ расходующихся и плюс (+) для образующихся.

Для характеристики материального баланса многостадийных (сложных) реакций вводят безразмерную величину, называемую селективностью. Различают дифференциальную и интегральную селективности.

Интегральная селективность – это отношение количества реально полученного продукта j к его теоретическому количеству, которое могло бы образоваться из основного реагента А при отсутствии побочных реакций и потерь. Интегральную селективность для j по А записывают так:

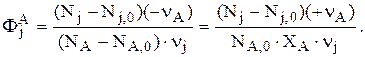
Например

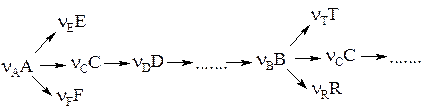
Тогда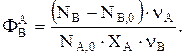

Если вещество j образуется из А по одной реакции, то 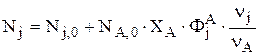или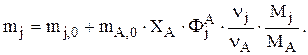

Такова связь между мольной и массовой интегральными селективностями. Аналогичные зависимости справедливы для мольных (F) и массовых (G) потоков. Если под j понимать В (целевой продукт), то уравнение используют для нахождения количества А на входе в реактор, например F_А,0, при заданной производительности G_В

.

По определению интегральная мольная селективность вещества j по А имеет вид:

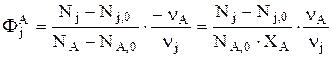, откуда следует:

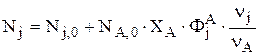или

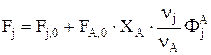
Если F_j задано и требуется определить F_A,0, то можно записать

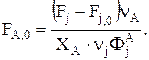
Соответственно, для массовых потоков имеем:

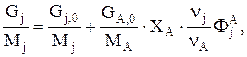откуда

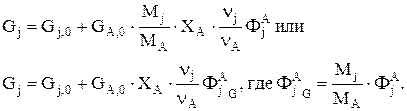
Селективность можно определить как отношение скорости целевой реакции (скорости образования целевого продукта) к общей скорости процесса (скорости расходования реагента). Рассчитанную таким образом селективность дифференциальной.

где r_цел.р. – скорость расходования реагента по целевой реакции; r_общ. – суммарная скорость расходования реагента.

Пример. Учебник стр.28-30