Арифметические выражения

Приведем примеры записи арифметических выражений на Фортране:

Математическая формула	Арифметическое выражение на Фортране
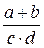	(a+b)/(c*d)
p+q sin2a	p+q*sin(a)**2
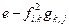	e-f(i,k)**2*g(k,j)

Для того чтобы правильно записывать арифметические выражения, нужно соблюдать следующие правила:

1. Все символы пишутся в строчку на одном уровне. Проставляются все знаки операций (нельзя пропускать *).

2. Не допускаются два следующих подряд знака операций. (Нельзя A + – B; можно A + (–B).)

3. Операции с более высоким приоритетом (рангом) выполняются раньше операций с меньшим приоритетом.

4. Вычисление функции имеет более высокий ранг, чем арифметические операции. Аргумент функции – выражение, стоящее в круглых скобках после имени функции.

5. Операции одного ранга выполняются слева направо (возведение в степень – справа налево).

6. Часть выражения, заключенная в скобки, вычисляется в первую очередь. (Например, (A+B)*(C–D) — умножение производится после сложения и вычитания.)

Не следует записывать выражений, не имеющих математического смысла :

· деления на нуль;

· возведения нулевого значения в отрицательную или нулевую степень;

· возведения отрицательного операнда в нецелочисленную степень.

В таких ситуациях происходит прерывание работы процессора.

При переносе длинного выражения на следующую строку нельзя повторять знак операции.

Пример. Цифрами сверху указан порядок выполнения операций:

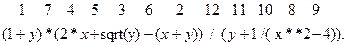
Данное арифметическое выражение соответствует следующей математической формуле:

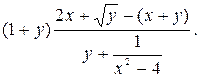
Преобразование типов операндов при вычислении выражений.При выполнении двухместной операции

A знак B :

– если типы А и В одинаковые, то и тип результата – тот же;

– если типы А и В разные, то сначала происходит преобразование операнда с младшим типом к старшему типу, затем выполняется операция. Результат получит старший тип.

Числовые типы в порядке возрастания старшинства расположены так:

целый (I) – вещественный (R) – комплексный (C).

Внутри каждого типа старшинство растет с ростом разновидности.

Особенности вычислений с целыми числами.Рассмотрим простую программу:

real(4) c1, c2

c1=3/2; c2= -3/2

print *,c1,c2 ! 1.0 -1.0

End

Операнды – целые числа, поэтому и результат должен быть целым числом - целой частью результата обычного деления. Затем, поскольку c1, c2 имеют тип real(4), целые числа 1 и –1 преобразуются в стандартный вещественный тип.

Если один из операндов сделать вещественным, то результатом деления также будет вещественное число, в данном случае – не равное единице:

c1=3./2 ! 3. – вещественная тройка

с2=float(3)/2 ! float – функция преобразования

! к вещественному типу

print *, c1,c2 ! 1.5 -1.5

Таким образом, чтобы получить правильный результат арифметического деления, достаточно сделать один из операндов формально вещественным.

Особенности возведения в степень. Возведение в целую степень компилятор реализует в виде серии последовательных умножений, а в действительную – через логарифмирование основания, умножение на показатель степени и вычисление показательной функции:

x⁵=x*x*x*x*x x ^1,2 = e ^1,2*^ln(x)

Тип показателя степени определяется по формальным признакам. Поэтому возведение в степени 2 и 2.0, также в целую степень k и вещественную степень y при одинаковом числовом значении названных переменных будет производиться разными способами.

Для вычисления значения квадратного корня рекомендуется использовать не операцию возведения в степень 0.5, а стандартную функцию sqrt.

Особенности вычислений с разнопорядковыми величинами. Ограниченность разрядности и диапазона чисел, представимых в любой ЭВМ, делает порядок выполнения операций одинакового приоритета не вполне безразличным. Например:

real(4):: a=1.0e+32, b=-1.0e+32, c=7.0

print *,a+b+c ! 7.000000 (верный результат)

print *,a+c+b)! 0.000000E+00 (потеря значимости)

При сложении чисел с существенно различными порядками нужно учитывать возможную потерю значимости меньшего по модулю в процессе выравнивания порядков.

Сложение чисел одного знака во избежание потери точности следует начинать со слагаемых, меньших по модулю. В процессе накопления произведения при неудачном выборе пар сомножителей можно получить переполнение разрядной сетки, или "машинный нуль". Нужно стремиться к тому, чтобы каждое очередное произведение было по модулю возможно ближе к единице.

Встроенные функции.Естественным требованием к языку, ориентированному на научные приложения, является достаточно богатый набор встроенных, т.е. являющихся частью языка, функций и процедур.

Каждая функция имеет родовое и специфическое имя. При использовании родового имени тип функции определяется типом аргумента. Специфическое имя ориентировано на строго определенный тип аргумента и результата. В таблице приведены основные математические функции с родовыми именами. Использованы обозначения типов: I – целый, R – вещественный, C – комплексный.