Случай равноотстоящих узлов

Пусть , .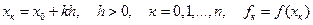

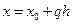Подставив эти выражения в (10.3), получаем

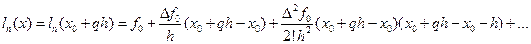
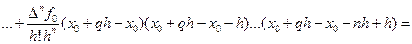
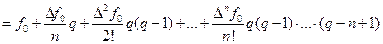. (10.4) Выражение (10.4) называется интерполяционным многочленом Ньютона для интерполяции вперед.

Начало отсчета в нем расположено в крайнем левом узле 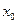(здесь 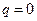). Интерполяционный многочлен (10.4) удобно использовать в начале таблицы и для экстраполяции левее точки 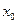, т.е. для .

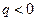Рассмотрим пример интерполяции по формуле (10.4).

Пусть дана таблица значений функции 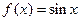и ее конечных разностей.

Конечные разности для простоты принято выписывать в числе единиц последнего десятичного знака, т.е. без указания положения запятой.

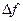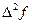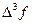5 7 9 11 13 15	0,087156   0,121869   0,156434   0,190809   0,224951   0,258819	-34713   -34565   -34375   -34142   -33868	-148   -190   -233   -274	-42   -43   -41

Допустим, что надо найти 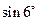. Из таблицы видно, что третьи разности близки к постоянной. Это свидетельствует о том, что функция 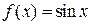на рассматриваемом промежутке близка к некоторому алгебраическому многочлену третьей степени.

Положим в (10.4) .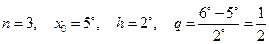

Вычисления имеют вид:

, ,

, ,

.

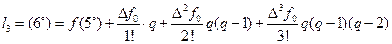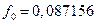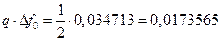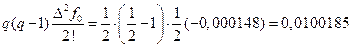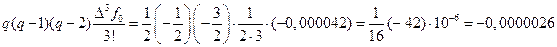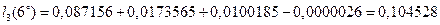
Промежуточные значения находились с семью знаками после запятой. Седьмой является запасным, в окончательном результате он округлен.

Для справки, точное значение 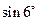, округленное с шестью знаками после запятой, равно 0,104528. т.е. все выписанные знаки для 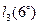получились верные.

Для интерполяционного многочлена Ньютона при интерполяции назад начало отсчета 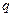расположено в крайнем правом узле 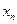, а используемые конечные разности идут в таблице от 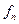вправо вверх:

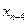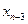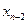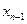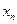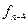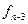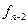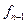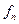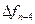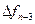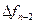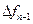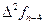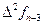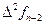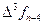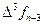Интерполяционный многочлен с узлами 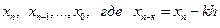, имеет вид

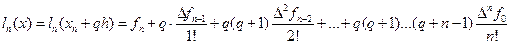. (10.5)

Этот многочлен называется интерполяционным многочленом Ньютона для интерполяции назад.

Обратное интерполирование.

а). Пусть функция задана таблицей.

Задача обратного интерполирования заключается в том, чтобы по заданному значению функции определить соответствующее значение аргумента .

Будем считать, что в рассматриваемом интервале функция монотонна. Следовательно, задача имеет единственное решение. Она решается с помощью интерполяционного многочлена Лагранжа. Для этого надо принять переменную за независимую, а считать функцией от . Написав по заданным узлам 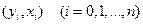многочлен Лагранжа, можно определить по заданному . Остаточный член можно получить из остаточного члена формулы Лагранжа, меняя местами и

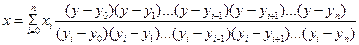. (10.6)

б). Итерационные методы. Если функция 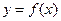задана в виде таблицы с равноотстоящими узлами, то для нее можно записать один из интерполяционных многочленов. Например, первый интерполяционный многочлен Ньютона:

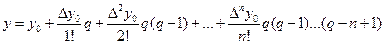. (10.7)

Рассматривая последнее выражение как уравнение относительно 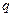, находим 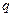по заданному значению , а затем вычисляем

.

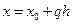Если число узлов велико, то получим алгебраическое уравнение высокой степени. При решении такого уравнения удобно применить метод итераций.

Для этого запишем уравнение (10.7) в виде

.

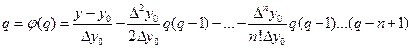За начальное приближение принимаем 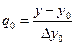, а затем применяем процесс итераций 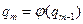. При достаточно малом шаге 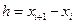процесс итераций сходится к искомому корню, т.е. .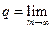

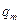Условием сходимости является выполнение неравенства .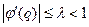

На практике итерации продолжают до тех пор, пока два последовательных значения 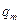и 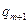не совпадут с заданной точностью, и полагают .

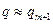11. Интерполирование сплайнами.

Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или просто сплайном называют кусочно-полиномиальную функцию, определенную на отрезке и имеющую на этом отрезке некоторое число непрерывных производных.

Рассмотрим частный, но распространенный в практике случай, когда сплайн определяется с помощью многочленов третьей степени (кубический сплайн).