Вычисление значений синуса и косинуса

С помощью формул приведения аргумент х можно заключить в промежуток: 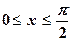. Если 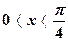, то имеем:

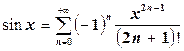. (5.18)

Eсли же 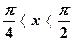, то полагают:

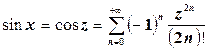, (5.19)

где 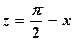и .

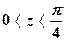Сумму ряда (5.18) удобно вычислять суммированием

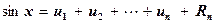, (5.20)

где слагаемые 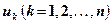последовательно находятся с помощью рекуррентного соотношения:

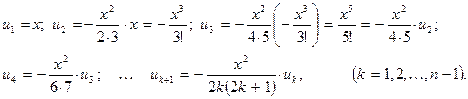
Т.к. ряд (5.18) знакочередующийся с монотонно убывающими по модулю членами, то на основании теоремы, приведенной выше, справедлива оценка

;

.

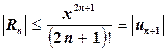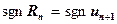Как только будет обнаружено, что 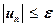, процесс суммирования можно прекратить; e - заданная остаточная погрешность.

Аналогично ,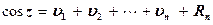

где ,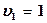

;

.

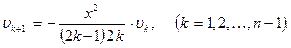
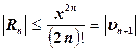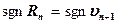Вычисление значений гиперболического синуса

Как известно,

,

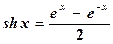причем ,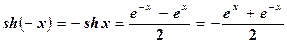

т.е. функция shx - нечетная.

Для гиперболического синуса справедливо разложение

.

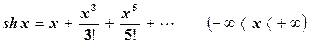Предполагая, что х > 0, вычисления удобно производить суммированием:

,

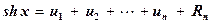где 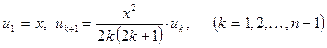и R_n – остаточный член. При 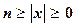имеем:

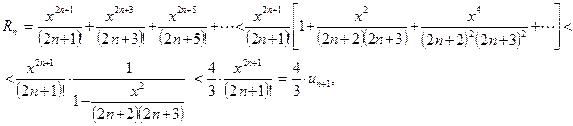
так как 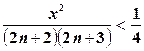при .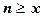

Очевидно, что 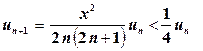при .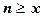

Поэтому 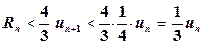, то есть .

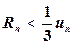Вычисление значений гиперболического косинуса.

Как известно,

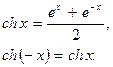
Для гиперболического косинуса справедливо разложение:

.

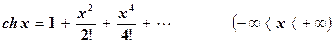Вычисления удобно производить процессом суммирования:

,

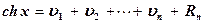где 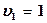, 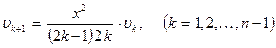и R_n – остаточный член. При 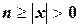имеем:

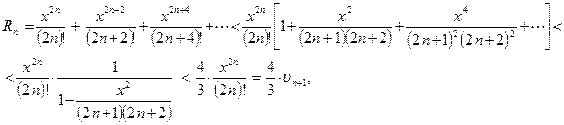
Так как при n ³ 1 справедливо неравенство

,

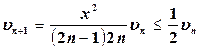то .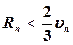

Применение метода итерации для приближенного вычисления

Значений функции

Пусть требуется вычислить значение непрерывной функции

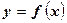. (5.20¢)

Запишем функцию (5.20¢) в неявном виде

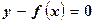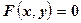или , где 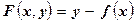(5.21)

Предположим, что 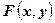непрерывна и имеет непрерывную частную производную 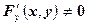. Пусть y_n – приближенное значение у. Применяя теорему Лагранжа, будем иметь:

,

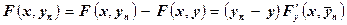где 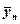- некоторое промежуточное значение между у_п и у. Отсюда

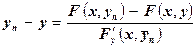. Т.к. 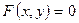, то

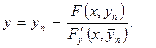(5.22)

Значение 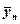нам неизвестно. Полагая 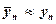, для вычисления значения 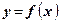получим итерационный процесс

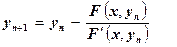
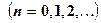. (5.23)

Формула (5.23) имеет простой геометрический смысл. Зафиксируем значение х и рассмотрим график функции 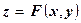(5.24)

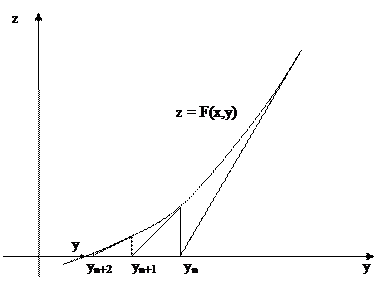
Рис.5. 2. Графическое представление метода итераций.

Из формулы (5.23) вытекает, что наш процесс представляет собой метод Ньютона, примененный к функции (5.24), т.е. последовательные приближения у_п+1 получаются как абсциссы точки пересечения с осью ОУ касательной к кривой (5.24), проведенной при 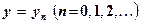(см. рис.2). Сходимость процесса обеспечивается, есл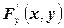и и 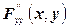сохраняют постоянные знаки в рассматриваемом интервале, содержащем корень у.

Начальное значение у₀ произвольно и выбирается по возможности близким к искомому значению у. Процесс итерации продолжается до тех пор, пока в пределах заданной точности e два последовательных значения у_п и у_п-1 не совпадут между собой: 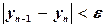. При этом, строго говоря, не гарантируется, что

,

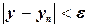поэтому в каждом конкретном случае требуется дополнительное исследование.