Приближенные числа и действия с ними
Погрешности и их классификация
Решение, получаемое численным методом, обычно содержит некоторую погрешность. Ее источниками являются: 1) несоответствие математической задачи (математической модели) изучаемому реальному явлению; 2) погрешность исходных данных (входных параметров); 3) погрешность метода решения; 4) вычислительная погрешность (погрешность округлений).
Погрешность в решении, вызванная первыми двумя источниками, называется неустранимой. Эта погрешность присутствует всегда, подобно погрешности функции, возникающей за счет погрешности аргументов.
Погрешность метода возникает в силу того, что численные методы сами по себе являются приближенными, т.е. даже если бы не было источников неустранимых погрешностей и не было бы погрешностей округления, то решение задачи все равно содержало бы погрешность. Отчасти это происходит потому, что численным методом обычно решается другая, более простая задача, аппроксимирующая (приближающая) исходную задачу. В ряде же случаев используемый численный метод строится на базе бесконечного процесса, прерываемого на некотором шаге, что дает лишь приближенное решение.
В численных методах изучению погрешности метода уделяется значительное внимание. Зная зависимости погрешности метода от контролируемых параметров, можно принимать соответствующие меры по оптимизации этих параметров с целью уменьшения погрешности. Очевидным путем уменьшения погрешности решения является выбор такого метода, который дает наименьшие погрешности по сравнению с другими методами.
Технически наиболее сложным является вопрос учета погрешностей округления в арифметических действиях. При ручных вычислениях, когда действий немного, погрешности округления учитываются с помощью способов, изложенных ниже. Они основываются на элементарной теории погрешностей. Примерно такая же ситуация складывается и при машинных расчетах, когда число действий относительно невелико (например, несколько тысяч). Здесь погрешности округления не проявляются, так как в ЭВМ числа представляются с десятью и более десятичными значащими цифрами, а окончательный результат редко бывает нужен более чем с 5 десятичными значащими цифрами.
В случае же, когда задача требует для своего решения, скажем, 107 и более арифметических действий, учет влияния погрешностей округления в каждом действии не реален. При таком учете получится слишком завышенная оценка предельной погрешности, так как ей отвечают самые неблагоприятные случаи, когда от действия к действию абсолютные погрешности накапливаются. В действительности погрешности округления ведут себя достаточно случайно как по величине, так и по знаку. Поэтому есть предпосылки для их взаимной компенсации.
Для решения одной и той же задачи могут применяться различные приближенные методы, в которых чувствительность к погрешностям округления различна.
Выбор численного метода. Численный метод может считаться удачно выбранным, если погрешность метода в несколько раз меньше неустранимой погрешности, а погрешность, возникающая за счет округлений, по крайней мере, в несколько раз меньше погрешности метода.
Если неустранимая погрешность отсутствует, то погрешность метода должна быть несколько меньше заданной точности решения.
К численным методам предъявляется еще ряд других требований. Предпочитается метод, реализуемый с помощью меньшего числа действий, требующий меньшей памяти ЭВМ, являющийся логически более простым (т.е. более быстрая реализация на ЭВМ). Обычно перечисленные требования противоречат друг другу, поэтому часто при выборе численного метода приходится соблюдать компромисс между ними.
Приближенные числа и действия с ними.
Пусть а – точное числовое значение некоторой величины; а* - приближенное числовое значение этой величины. Величина
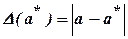 (2.1)
(2.1)
называется абсолютной погрешностью приближенного числа а*, а величина
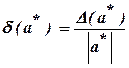 (2.2)
(2.2)
называется его относительной погрешностью.
Любое число 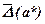 , о котором известно, что
, о котором известно, что
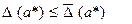 (2.3)
(2.3)
называется предельной абсолютной погрешностью приближенного числа а*.
Любое число 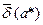 , о котором известно, что
, о котором известно, что
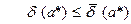 (2.3')
(2.3')
называется предельной относительной погрешностью приближенного числа а*.
По определению принято, что 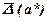 и
и 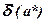 связаны отношением
связаны отношением 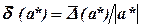 .
.
