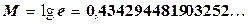Вычисление значений аналитической функции

Действительная функция f(x) называется аналитической в точке x, если в некоторой окрестности 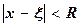этой точки функция разлагается в степенной ряд (ряд Тейлора):

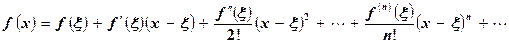(5.6)

Разложение f(x) в ряд Тейлора является удобным способом вычисления значений этой функции.

Если f(x) известно и требуется найти значение 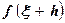, где h – «малая поправка», то формулу (5.6) выгодно записывать в виде

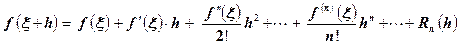(5.7),

где 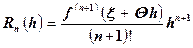(0 <Q < 1) (5.8)

Подставляя значение h в (5.7), мы получаем задачу, решение которой подробно разбиралось выше (см. «нахождение сумм числовых рядов»).

Вычисление значений показательной функции

Для экспоненциальной функции e^x справедливо разложение

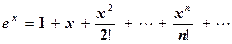, (5.9)

интервал сходимости которого -¥ < x +¥. Остаточный член ряда имеет вид

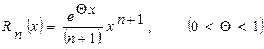(5.10)

При больших по модулю значениях х ряд (5.9) мало пригоден для вычислений. Поэтому поступают следующим образом: пусть

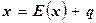
(5.11),

где Е(х) – целая часть числа х и 0 £ q < 1 – дробная его часть. Имеем

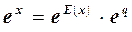(5.12)

Первый множитель е^Е может быть получен умножением:

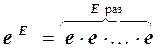, если Е > 0

или 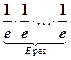, если Е< 0.

е или 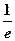берут с достаточной точностью, т.е. погрешность в определении е или 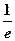<< e - заданной точности:

е = 2, 718281828459045¼

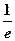= 0,36787944117442¼

Второй множитель в (5.12) е^q вычисляется с помощью разложения (5.9)

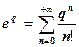, (5.13)

которое при 0 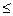q < 1 образует быстро сходящийся ряд.

Для остаточного члена R_n (q) получаем оценку из (5.10).

Так как 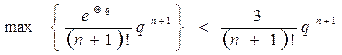, то при Q = 1 и q = 1

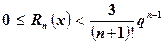
Последующие вычисления ведутся аналогично вычислениям при нахождении суммы ряда.

Вычисление значений логарифмической функции

Для натуральных логарифмов чисел, близких к единице, справедливо разложение

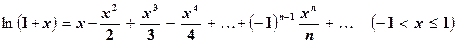. (5.14)

Формула (5.14) малопригодна для вычислений, так как диапазон чисел 0 < 1 + x £ 2 не велик и, кроме того, при 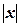, близком к единице, ряд (5.14) сходится медленно.

Существует более удобная формула для вычисления натуральных логарифмов. Выведем ее.

Заменяя х в формуле (5.14) на –х, будем иметь

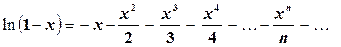(5.15)

Вычтем почленно (5.15) из (5.14)

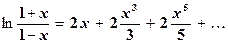или .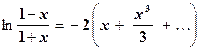

Сделаем замену

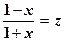, или .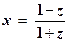

Тогда

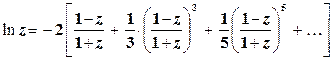(5.16)

при 0 < z < +¥.

Пусть х – положительное число. Представим его в виде

,

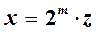где m – целое число и 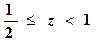. Тогда, полагая

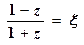, где 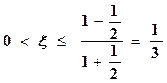, и применяя формулу (5.16), имеем

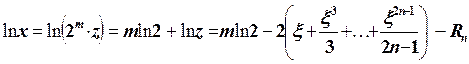(5.16¢)

где

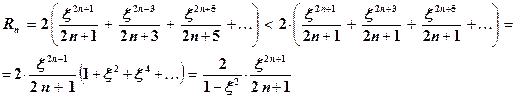
При 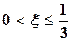имеем 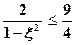и поэтому

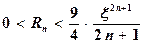(5.17)

или, более грубо,

.

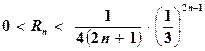Число членов п находится из соображений, приводимых раньше при вычислении суммы рядов.

Пример. Найти ln 3 с точностью до 10^-5.

Решение. Вычисления будем производить с двумя запасными знаками. Положим .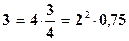

Отсюда z = 0,75 и

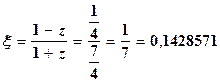
Имеем

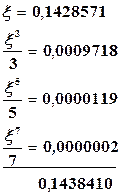
Используя формулу (5.16¢) и учитывая, что ln 2 = 0,69314718¼, получаем

ln 3 = 2 × 0,69314718 - 2 × 0,1438410 = 1,09861.

Замечание 1. Можно также вычислять натуральные логарифмы чисел, исходя из представления

,

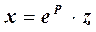где Р – целое число и .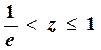

Замечание 2. Для вычисления десятичных логарифмов используется формула

,

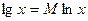где