Уменьшение погрешностей

Выше, при рассмотрении погрешностей, мы убедились, что практически любые арифметические операции приводят к увеличению погрешностей. Но в разных ситуациях это происходит по-разному. Особенно к быстрому увеличению относительной погрешности приводит вычитание близких чисел. Поэтому в алгоритмах следует избегать таких и подобных ситуаций.

Рассмотрим еще несколько примеров, показывающих источник подобных погрешностей и возможные пути их исключения в вычислениях за счет правильной организации.

а) Пусть требуется найти сумму пяти чисел:

S = 0,2764 + 0,3944 + 1,475 + 26,46 + 1364.

Простым сложением («ручным») с последующим округлением получаем S = 1393. Но при вычислении на машине округление происходит после каждого сложения. Предполагая условно сетку четырехразрядной, проследим вычисление на машине суммы чисел от наименьшего к наибольшему, т.е. в порядке их записи:

0,2764 + 0,3944 = 0,6708; 0,6708 + 1,475 = 2,156;

2,156 + 26,46 = 28,62; 28,62 + 13,64 = 1393 = S₁.

Итак, получили верный результат.

Изменим теперь порядок суммирования:

1364 + 26,46 = 1390; 1390 + 1,475 = 1391;

1391 + 0,3944 = 1391; 1391 + 0,2764 = 1391 = S₂.

Видим, что S₁ ¹ S₂.

На данном простом примере причины потери точности очевидны: она происходит из-за того, что прибавления к большому числу малых чисел не происходит, т.к. они выходят за рамки разрядной сетки 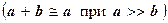. Этих малых чисел может быть очень много и в результате сложения погрешность накапливается.

В подобных вычислениях надо соблюдать правило: сложение чисел нужно проводить по мере их возрастания. Подобного рода «маленькие хитрости» в машинной практике могут потребоваться в любой момент для улучшения алгоритма и снижения погрешностей результатов.

б) Еще один пример в продолжение предыдущего.

При вычислении на ЭВМ значения 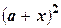может оказаться, что x << a, и результатом сложения а + х получится а. В этом случае может помочь замена:

.

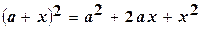в) Рассмотрим следующий пример – использование рядов для вычисления значений функций. Пусть раскладывается в ряд функция sinx по степеням х:

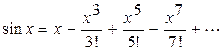
Вычислим значение функции при х = 0,5236 (радиан), что соответствует 30°. При вычислениях члены ряда, меньшие 10^-4, учитывать не будем (к данному ряду применима теорема Лейбница, поэтому погрешность будет £ 10^-4). Проведя вычисления с четырьмя верными знаками, получим

sin 0,5236 » 0,5236 – 0,2393 × 10^-1 + 0,3281 × 10^-3 = 0,500.

Из курса высшей математики мы знаем, что данный ряд имеет радиус сходимости 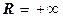, т.е. по этой формуле мы можем разложить sinx по любому аргументу. Нам интересно ее разложить для х = 30° + 360° = 390° = 6,807 (радиан). Опуская подробные вычисления, даем результат sin 6,807 » 0,5493. Относительная погрешность составила здесь около 10%, что объясняется погрешностями округлений и способом суммирования ряда (слева направо, без учета величины членов).

Конечно, можно было попытаться повысить точность вычислений. Но в данном примере даже при учете членов ряда до 10^-8 и вычислениях с восемью значащими цифрами при х = 25,66 (радиан) = 4·360° + 30° в результате аналогичных вычислений получается результат, не имеющий смысла: sin 25,66 @ 24.

Поэтому в программах, использующих степенные ряды для вычисления значений функций, должны быть приняты соответствующие меры по предотвращению подобной потери точности. Так, для тригонометрических функций можно использовать формулы приведения, благодаря чему х окажется в интервале ½х½ < 1, при этом резко ускорится сходимость ряда.

В других случаях, например, при вычислении экспоненты аргумент х можно разбить на сумму целой и дробной частей: 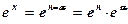, где n – целая часть х, a - ее дробная часть. 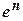вычисляют умножением, 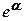- разложением в ряд.

Таким образом, при организации вычислений надо стараться своевременно распознать «подводные камни» и соответствующим образом их обойти.

Разумеется, описанные выше примеры потерь точности не охватывают и малой части тех возможных ситуаций, которые встречаются в практических вычислениях. Кроме того, реальные ситуации могут оказаться и значительно сложнее описанных случаев.