Классический метод расчета

1. Правила коммутации:

i_L(0_–) = i_L(0₊) = 0 А,

u_C(0_–) = u_C(0₊) = J R₂ = 20 B.

Составление характеристического уравнения цепи.

2.1. Совместное решение однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:

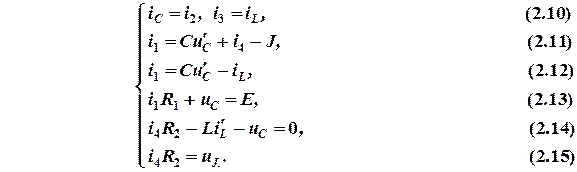Из уравнения (2.12)

.

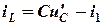Из уравнения (2.13) определим ток

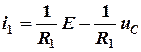(2.17)

И подставим его в выражение для тока индуктивности

.

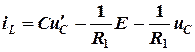Определим производную тока индуктивности

.

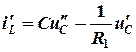Из уравнения (2.11) определим ток i₄

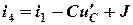
И подставим в полученное уравнение (2.17)

.

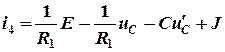Все полученные выражения подставляем в уравнение (2.14)

.

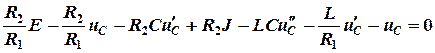После приведения подобных слагаемых и группирования получаем дифференциальное неоднородное уравнение второго порядка

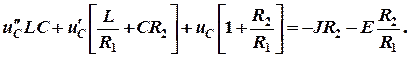
Таким образом методом исключения из системы дифференциальных уравнений для любой электрической цепи можно получить дифференциальное неоднородное уравнение.

Характеристическое уравнение получается из соответствующего однородного дифференциального уравнения в результате замены производных на соответствующие степени оператора p и имеет вид

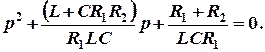
2.2. Алгебраизация дифференциальных уравнений. Для получения характеристических уравнений записывается система уравнений по методу контурных токов, которая впоследствии переписывается в алгебраической форме с помощью вспомогательного символа p, заменяющего операцию дифференцирования, и 1/p, заменяющего операцию интегрирования:

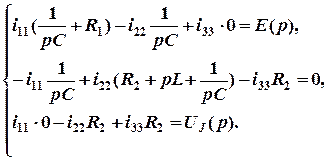
Так как i₃₃ = J , следовательно,

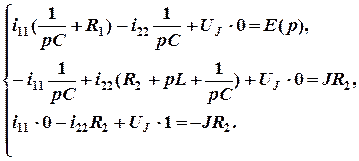
и, соответственно, для свободных составляющих токов:

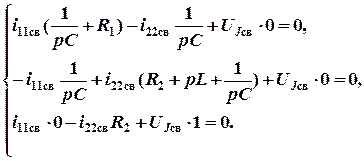
Данная система алгебраических уравнений имеет решение, отличное от нулевого только тогда, когда ее определитель равен нулю:

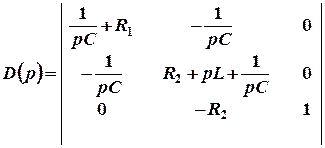
Или

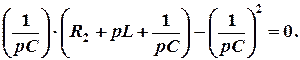
Таким образом, характеристическое уравнение в результате преобразования принимает вид

.

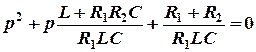Метод входного сопротивления. Удалим источники из цепи в соответствии с известным правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются.

В произвольной ветви, разорвав цепь, запишем входное сопротивление:

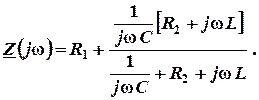
Заменив jw на p, получим

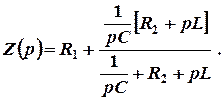
Приравняв данное выражение нулю (Z(р) = 0) и произведя необходимые преобразования, получим характеристическое уравнение цепи

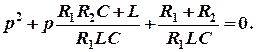
Подставим значения параметров цепи:

p² + 700p + 300000 = 0.

Корни характеристического уравнения

p₁ = – 350 + j421,308, p₂ = – 350 – j421,308

Являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер.

5. Определение принужденной составляющей. Рассматриваемая цепь в принужденном режиме имеет вид (рис. 2.4)

,

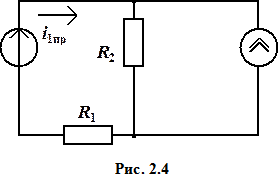
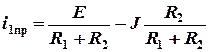i_1пр = 1/3 (A).