ЛАБОРАТОРНАЯ РАБОТА № 1. СИТОВЫЙ АНАЛИЗ СЫПУЧЕГО МАТЕРИАЛА, ПОСТРОЕНИЕ ХАРАКТЕРИСТИК КРУПНОСТИ

СИТОВЫЙ АНАЛИЗ СЫПУЧЕГО МАТЕРИАЛА, ПОСТРОЕНИЕ ХАРАКТЕРИСТИК КРУПНОСТИ

Цель работы: Освоение методики производства ситового анализа, расчета и оформления его результатов, определение с помощью характеристик крупности выходов заданных классов.

Инструмент, приборы и оборудование:Механический встряхиватель с тремя наборами сит (сита с размером отверстий 0,50; 0,25; 0,10; 0,071 мм); технические весы; набор гирь; секундомер; совок для отбора проб; чашки пластмассовые для взвешивания проб и полученных в результате рассева классов; исследуемый материал крупностью 0-1 мм.

Общие сведения

Материалы, с которыми приходится иметь дело при дроблении, измельчении, грохочении и обогащении полезных ископаемых, представляют собой смеси зерен (кусков) минералов различного размера. Размеры эти колеблются от сотен мм до нескольких мкм. Поскольку куски имеют неправильную форму, то их величина может быть охарактеризована несколькими размерами. Однако для практических целей величину куска желательно характеризовать одним эквивалентным размером, так называемым “диаметром”.

Метод определения размера частицы (куска) выбирается в зависимости от способа измерений и целей, для которых этот диаметр подсчитывается.

При грохочении для массовых определений размера зерна за диаметр зерна принимают размер наименьшего квадратного отверстия, через которое это зерно может проходить. Крупность всей массы сыпучего материала оценивают по содержанию в ней классов определенной крупности, т.е. по ее гранулометрическому составу.

Гранулометрический состав материалов для контроля процессов грохочения, дробления и измельчения на обогатительных фабриках определяют чаще всего посредством ситового анализа.

Рассев сыпучего материала с целью определения его гранулометрического состава называется ситовым анализом. Ситовый анализ заключается в просеивании пробы через стандартный набор сит и в определении процентного содержания остатка на каждом из них по отношению к массе исходной пробы.

Для облегчения просеивания применяют механические устройства (рис.1.1), в которых закрепленный набор сит совершает вращательное движение с одновременным встряхиванием. Выделение классов при грохочении производят по схеме от “крупного к мелкому” (рис.1.2).

Результаты ситового анализа заносят в типовую таблицу. По данным таблицы ситового анализа строят характеристику крупности.

Характеристика крупности - это графическое изображение гранулометрического состава сыпучего материала.

Суммарные характеристики крупности “по +d ” могут быть выпуклыми, вогнутыми и прямолинейными (рис. 1.3): выпуклая кривая 3 говорит о преобладании в материале крупных зерен, вогнутая 1 - мелких зерен, прямолинейная 2 - о равномерном распределении в материале зерен по крупности.

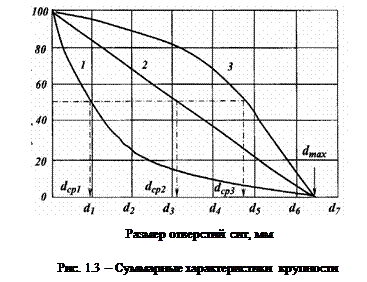
По кривой суммарной характеристики крупности можно определить выход любого класса.

При построении суммарных характеристик крупности в широком диапазоне крупности зерен материала отрезки на оси абсцисс в области мелких классов получаются весьма малого размера, что затрудняет построение и использование характеристик. Чтобы не строить больших графиков, суммарные характеристики строят в системе координат с полулогарифмической (рис. 1.4) или логарифмической шкалой.

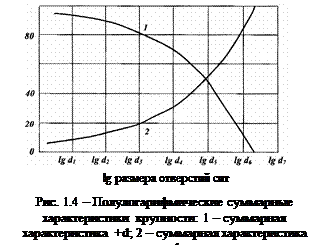
Логарифмическая характеристика позволяет в некоторых случаях установить наличие закономерностей распределения в материале зерен по крупности. Для дробленных и измельченных мономинеральных пород логарифмическая характеристика, построенная “по -d ”, большей частью получается прямолинейной.

Уравнение прямой линии в логарифмических координатах имеет вид:

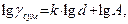(1.1)

где g_сум - суммарный выход классов мельче отверстий сита, %;

k - коэффициент, равный тангенсу угла наклона прямой;

d - диаметр отверстий сита, мм;

lg А - отрезок, отсекаемый прямой на оси ординат.

Используя антилогарифмы, уравнение (1.1) можно преобразовать:

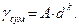(1.2)

Уравнение (1.2) суммарной характеристики, построенной “по минус d”, носит название уравнения Годэна-Андреева.

Величина коэффициента k определяет направление и степень изгиба кривой характеристики крупности. Если характеристика построена по “+ d” , то

- при k>1 – выпуклая характеристика, много крупных классов;

- при k=1 – прямая характеристика, равномерное распределение по классам;

- при k<1 – вогнутая характеристика, много мелких классов.

Из уравнения (1.2) следует, что при d = d_max → g_сум = 100%.

Тогда

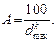(1.3)

Во многих случаях лучшее соответствие опытным данным дает уравнение Розина-Раммлера

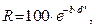(1.4)

где R – суммарный выход класса крупнее d ( по “+” ),%;

d – размер отверстий сита;

b и n – параметры, зависящие от свойств материала и размерности величины d.

При двойном последовательном логарифмировании уравнение приобретает вид:

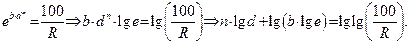
В координатах [lgd;lglg(100/R)] уравнение Розина – Раммлера изображается прямой линией с угловым коэффициентом n.

Уравнение Розина – Рамлера применяется при определении грансостава продуктов измельчения.