Порядок выполнения работы. АНАЛИЗ СВОЙСТВ СИСТЕМЫ ПОИСКА ЭКСТРЕМУМА

АНАЛИЗ СВОЙСТВ СИСТЕМЫ ПОИСКА ЭКСТРЕМУМА

СО СТАРШЕЙ ПРОИЗВОДНОЙ В УПРАВЛЕНИИ

Цель работы

Исследовать свойства градиентной системы поиска экстремума, основанной на методе локализации. Оценить влияние дифференцирующего фильтра и фильтра оценки частной производной на характер переходных процессов.

Основные сведения

В работе исследуется объект управления, который описывается уравнениями

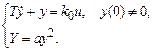(1.1)

На основании требований к процессу выхода на экстремум в замкнутой системе (t_п и σ %) формируется желаемое уравнение

.

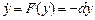С учетом градиента G = ∂Y/∂y, который для объекта (1.1) равен G = 2ay, желаемое уравнение может быть представлено в форме

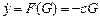, (1.2)

где с = d/2a. Поведение системы в статике будет описываться уравнением сG = 0, или G = 0, что соответствует выходу на экстремум. Согласно методу синтеза формируется управляющее воздействие

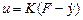, (1.3)

где K – коэффициент усиления регулятора, численное значение которого выбирается из диапазона

bK ≥ (20…100), .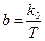

Для реализации закона управления (1.3) используется дифференцирующий фильтр, который при отсутствии помехи измерения описывается уравнением

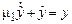, (1.4)

где 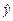и 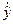являются оценками y и 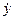соответственно; 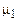– постоянная времени фильтра.

Оценка градиента G (частной производной в данном случае) осуществляется с помощью специального фильтра

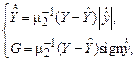(1.5)

где μ₂ – постоянная времени фильтра оценки частной производной (ФОЧП). Значения 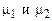следует выбирать с учётом условия разделимости движений по соотношению

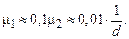(1.6)

Методические указания

3.1. Приступая к работе, необходимо предварительно (в соответствии с номером варианта) сформировать желаемое дифференциальное уравнение, а также определить параметры дифференцирующего фильтра и фильтра оценки частной производной.

3.2. Для исследования свойств системы в качестве метода интегрирования рекомендуется выбрать метод Рунге-Кутта 4-го порядка.

3.3. При исследовании быстрой переменной 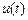необходимо задавать время наблюдения не более 0,05 с.

Порядок выполнения работы

4.1. Определить параметры регулятора и фильтров на основании требований к качеству работы системы (табл. 1.1).

Т а б л и ц а 1.1

Параметр	Вариант
k0
T
a	0,8		0,5	0,6		0,5	0,9

4.2. Собрать модель замкнутой системы (рис. 1.1) и зарисовать переходные процессы y(t), Y(t) и G(t), задавая начальные условия 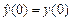=2, а .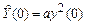

4.3. Рассмотреть траекторию движения системы на плоскости (y, Y).

4.4. Исследовать влияние регулятора на y(t) и u(t) при тех же начальных условиях, изменяя K в диапазоне (1…50).

4.5. Оценить влияние начальных условий дифференцирующего фильтра на y(t), Y(t) и G(t), уменьшая и увеличивая 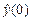в
1,5 раза относительно номинального значения. Построить траектории движения системы на плоскости (y, Y).

4.6. При 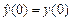исследовать влияние начальных условий ФОЧП на y(t), Y(t) и G(t), изменяя 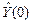в диапазоне
(0,6…5) .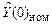

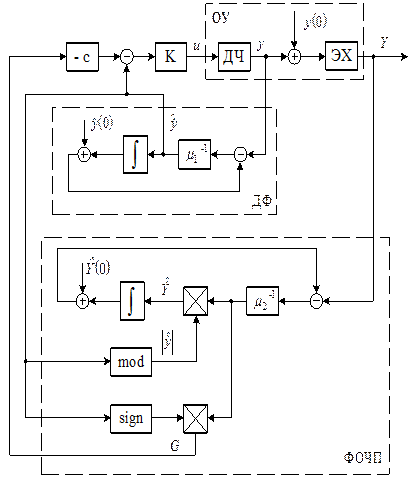
Рис.1.1. Структурная схема системы поиска экстремума

4.7. Исследовать влияние параметра с на характер процессов, уменьшая и увеличивая его значение в 5 раз при исходных значениях начальных условий ДФ и ФОЧП. Сравнить результаты с процессами, полученными в п. 4.1. Зарисовать переходные процессы y(t), Y(t) и G(t).

4.8. Пр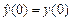и и 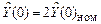исследовать влияние m₂ на y(t), Y(t) и G(t), увеличивая его значение в 5 раз относительно расчетного.

4.9. Пр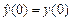и и 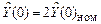оценить влияние m₁ на процессы в системе, увеличивая его значение в 5 раз относительно расчетного.

Содержание отчета

5.1. Цель работы.

5.2. Результаты расчета параметров регулятора, фильтра оценки частной производной и дифференцирующего фильтра.

5.3. Структурная схема системы.

5.4. Графики всех переходных процессов и фазовых портретов.

5.5. Выводы по работе.

6. Контрольные вопросы

6.1. Как формируется закон управления в системах, основанных на принципе локализации?

6.2. Какова роль градиента в системах подобного типа?

6.3. С какой целью в систему вводится дифференцирующий фильтр?

6.4. Как оценить градиент с помощью ФОЧП?

6.5. Какое влияние оказывают малые инерционности фильтров на свойства замкнутой системы?

Лабораторная работа № 2