Основные правила преобразования структурных схем

1. Последовательное соединение звеньев (рис. 2.14, а). При последовательном соединении выходная величина каждого предшествующего звена является входным воздействием последующего звена. При преобразовании структурных схем цепочку из последовательно соединенных звеньев можно заменить одним звеном (рис. 2.14,6) с передаточной функцией 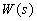, равной произведению передаточных функций отдельных звеньев .

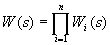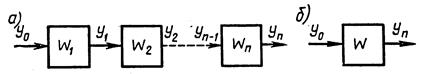
Рис. 2.14

2. Параллельное соединение звеньев (рис.2.15,а). При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь параллельно соединенных звеньев можно заменить одним звеном (рис.2.15,б) с передаточной функцией, равной сумме передаточных функций входящих в нее звеньев: .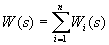

3. Звено, охваченное обратной связью (рис.2.16,а). Принято считать, что звено охвачено обратной связью, если его выходной сигнал через какое-либо другое звено подается на вход. При этом, если сигнал 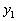обратной связи вычитается из входного воздействия 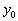( 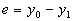), то обратную связь называют отрицательной. Если сигнал 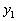обратной связи складывается с входным воздействием 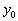( 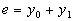), то обратную связь называют положительной.

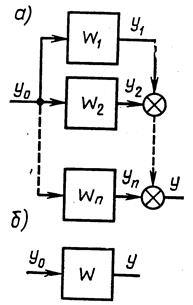
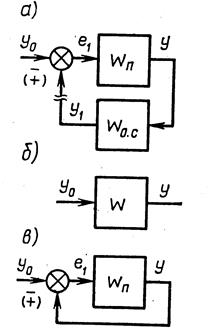
Рис. 2.15

Рис. 2.16

Передаточная функция 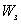замкнутой цепи с отрицательной обратной связью — звена, охваченного отрицательной обратной связью,— равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи

, .

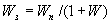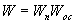Передаточная функция замкнутой цепи с положительной обратной связью равна передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи

, .

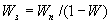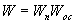Если передаточная функция 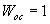, то обратная связь называется единичной и структурная схема изображается так, как показано на рис. 2.16,в. Передаточная функция при этом принимает вид 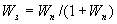при отрицательной обратной связи и 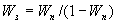— при положительной обратной связи.

При преобразовании структурных схем возникает необходимость переноса и перестановки сумматоров и узлов. Рассмотрим, какие изменения в схеме при этом нужно произвести.

4. Перенос сумматора (рис. 2.17). Легко показать, что при переносе сумматора по ходу сигнала необходимо добавить звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор (рис. 2.17, а). Если сумматор переносится против хода сигнала, то необходимо добавить звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор (рис. 2.17,б).

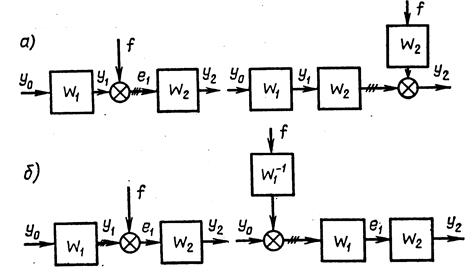
Рис. 2.17

При переносе сумматора возникают неэквивалентные участки линии связи. Эти участки на рис. 2.17 заштрихованы.

5. Перенос узла (рис. 2.18, а). При переносе узла также необходимо добавить звено. Если узел переносится по ходу сигнала, то добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел (рис. 2.18,б). Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел (рис. 2.18,в).

6. Перестановка узлов и сумматоров (рис. 2.19). Узлы можно переставлять местами (рис. 2.19 а). Точно так же можно переставлять сумматоры, не добавляя звена (рис. 2.19, б). При перестановке узла и сумматора (перенос узла через сумматор) необходимо добавить звено — суммирующее или сравнивающее (рис. 2.19, в, г).

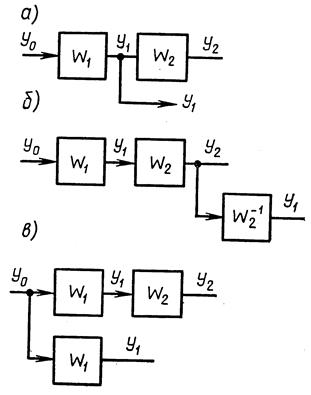
Рис. 2.18

Рис. 2.19

При переносе узла через сумматор, а также при перестановке сумматоров возникают неэквивалентные участки линии связи. Эти участки на рисунке заштрихованы.

Вычисление передаточной функции одноконтурной системы. Замкнутую систему (структурную схему) называют одноконтурной, если при ее размыкании в какой-либо точке получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных и обратных связей.

Рассмотрим одноконтурную систему, приведенную на рис. 2.20,а. Найдем передаточную функцию по входу g и выходу у. Участок по ходу сигнала от точки приложения входного воздействия до точки съема выходного сигнала назовем прямой цепью (рис. 2.20, а), а цепь из последовательно соединенных звеньев, входящих в замкнутый контур (рис. 2.20,б),— разомкнутой цепью. Как легко проверить, справедливо следующее правило: передаточная функция одноконтурной системы с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс(минус) передаточная функция разомкнутой цепи

,

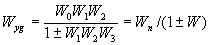где 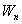— передаточная функция прямой цепи, 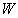— передаточная функция разомкнутой цепи. Сформулированное правило справедливо для любой одноконтурной системы.

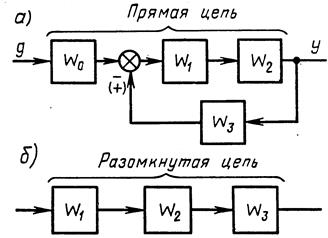
Рис. 2.20

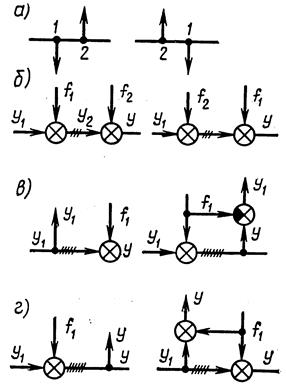
Вычисление передаточной функции многоконтурной системы. Замкнутую систему (структурную схему) называют многоконтурной, если при ее размыкании получается цепь, содержащая параллельные или обратные связи, или, иначе, замкнутую систему называют многоконтурной, если она помимо главной обратной связи содержит местные обратные или параллельные связи. Говорят, что многоконтурная система имеет перекрещивающиеся связи, если контур обратной или параллельной связи охватывает участок цепи, содержащий только начало или конец другой цепи обратной или параллельной связи (рис. 2.21,а,б).

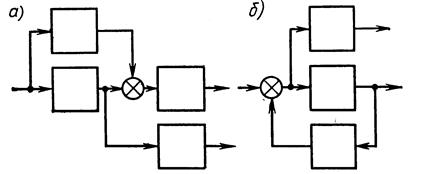
Рис. 2.21

Для вычисления передаточной функции многоконтурной системы необходимо прежде всего перестановкой и переносом узлов и сумматоров освободиться от перекрещивающихся связей. Затем, используя первые три правила преобразования структурных схем, преобразовать ее в одноконтурную систему, передаточную функцию которой, легко вычислить согласно сформулированному выше правилу. Следует иметь в виду, что при преобразовании структурной схемы нельзя переносить сумматор через точку съема выходного сигнала, так как при этом точка съема оказывается на неэквивалентном участке линии связи.

Пример 2.4. Найдем передаточные функции системы, приведенной на рис. 2.22,а, по “входам” g, f и “выходам” у и с. Эта система является многоконтурной с перекрещивающимися связями. Перенеся и переставив сумматоры, ее можно привести к многоконтурной системе без перекрещивающихся связей (рис. 2.22,б). После замены параллельно соединенных звеньев и звена, охваченного обратной связью, эквивалентными звеньями с передаточными функциями 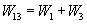, 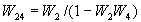получим одноконтурную схему (рис. 2.22,в).

При вычислении передаточной функции по входному воздействию g полагаем 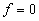. Согласно правилу вычисления передаточной функции одноконтурных систем имеем

.

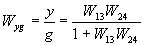При вычислении передаточной функции по входному воздействию f полагаем 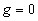. При этом сравнивающее звено становится инвертирующим эвеном с передаточной функцией, равной —1. Инвертирующее звено в замкнутый контур можно не вводить, если суммирующее звено преобразовать в сравнивающее звено. Поэтому в этом случае структурную схему можно представить так, как это показано на рис. 2.22,г. Из этой схемы очевидно

.
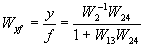