Контрольная работа № 9. «Элементы математической статистики, комбинаторики к теории вероятности»
Вариант 1
1. Вычислить:
a) 3!
b) 7! – 5!
c) 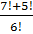
2. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
3. Сколькими способами можно расставить на одной полке 8 различных книг?
4. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найдите вероятность того, что из этих 5 деталей две окажутся бракованными.
5. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2, вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что а) оба элемента выйдут из строя, б) оба элемента будут работать.
Вариант 2
1. Вычислить:
а) 5!
б) 8! – 3!
в) 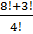
2. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
3.В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?
4. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?
5.Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.
Вариант 3
1. Вычислить:
а) 6!
б) 8! + 3!
в) 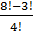
6. Из колоды в 36 карт вынимается одна. Какова вероятность появления карты червовой масти?
7. У нас есть 9 разных книг из серии «Занимательная математика». Сколькими способами можно расставить их на полке?
8. Студенты колледжа изучают в каждом семестре по десять дисциплин. В расписание занятий включается каждый день по 3 дисциплины. Сколько различных расписаний можно составить диспетчерская?
9.Группа из 5 женщин и 20 мужчин выбирает трех делегатов. Считая, что каждый из присутствующих с одинаковой вероятностью может быть выбран, найти вероятность того, что выберут двух женщин и одного мужчину.
Вариант 4
1. Вычислить:
а) 7!
б) 8! + 2!
в) 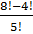
2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?
3. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.
4. В группе из 27 студентов нужно выбрать трех дежурных. Сколькими способами можно сделать?
5. В урне шары разного цвета: 20 белого, 15 черного, 5 синего. Найти вероятность того, что из урны наугад извлеченный шар окажется не белого или синего цвета?
