Контрольная работа № 5. «Решение неравенств»

Вариант 1

1. Решите систему неравенств:

.

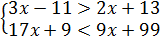2. Решите неравенства, применяя теоремы о равносильности:

.

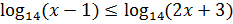3. Решите неравенство, методом введения новой переменной:

.

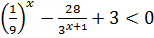4. Решите неравенство: .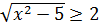

5. Решите неравенство: .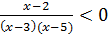

Вариант 2

1. Решите систему неравенств:

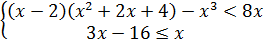
2. Решите неравенства, применяя теоремы о равносильности:

.

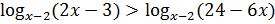3. Решите неравенство, методом введения новой переменной:

.

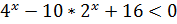4. Решите неравенство: .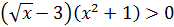

5. Решите неравенство: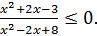

Вариант 3

1. Решите систему неравенств:

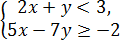
2. Решите неравенства, применяя теоремы о равносильности:

.

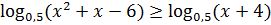3. Решите неравенство, методом введения новой переменной:

.

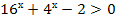4. Решите неравенство: .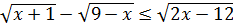

5. Решите неравенство: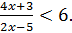

Вариант 4

1. Решите систему неравенств:

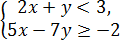
2. Решите неравенства, применяя теоремы о равносильности:

.

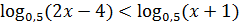3. Решите неравенство, методом введения новой переменной:

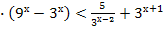
4. Решите неравенство: .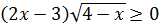

5. Решите неравенство: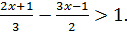

Контрольная работа № 6. «Производная и её применение»

Вариант 1

1. Найдите производную функции:

а) ;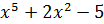

б) ;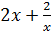

в) ;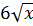

г) .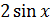

2. Найдите значение производной функции:

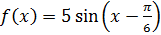в точке .

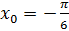3. Найдите точки графика функции 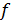, в которых касательная параллельна оси абсцисс:

.

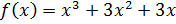4. Найдите наибольшее и наименьшее значения функции

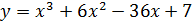на отрезке .

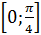5. Напишите уравнения касательных к кривой 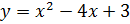, проходящих через точку М(2;-5).

Вариант 2

1. Найдите производную функции:

а) ;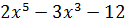

б) ;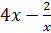

в) ;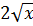

г). .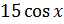

2. Найдите значение производной функции:

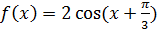в точке .

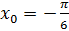3. Найдите точки графика функции 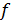, в которых касательная параллельна оси абсцисс:

.

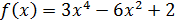4. Найдите наибольшее и наименьшее значения функции

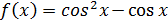на отрезке .

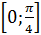5. Напишите уравнения касательных к кривой 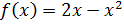, проходящих через точку М(-2; 3).

Контрольная работа № 7. «Первообразная и интеграл»

Вариант 1

1. Докажите, что F(х) = 2х⁴ – 3cosx является первообразной для функции f(x) = 8x³ + 3sinx.

2. Найдите неопределенный интеграл: ʃ ( - 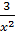+ 5cosx ) dx.

3. Вычислите интегралы:

a) ;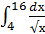

b) .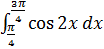

4. Вычислите площадь фигуры ограниченной линиями:

y = 1 + x³, y = 0, x = 2.

5. Вычислить площадь фигуры, ограниченной графиком функции

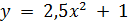, касательной к этому графику в точке с абсциссой х = 2 и прямой х = 0; фигура расположена в левой координатной плоскости.

Вариант 2

1. Докажите, что F(х) = 3х⁵ + 3 sin x является первообразной для функции f(x) = 15x⁴ + 3cosx.

2. Найдите неопределенный интеграл: ʃ (- 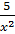- 3sinx) dx.

3. Вычислите интегралы:

a) ;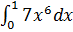

b) .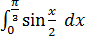

4. Вычислите площадь фигуры ограниченной линиями:

y = 4 – x², x = -1, x = 0.

5. Вычислить площадь фигуры, ограниченной графиком функции

y = -x³ + 3, касательной к этому графику в точке с абсциссой х = -2 и прямой х = 0; фигура расположена в левой координатной плоскости.

Контрольная работа № 8. «Степени и корни»

Вариант 1

1. Вычислите:

a)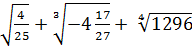

b)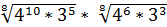

2. Упростите выражение: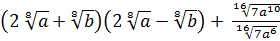

3. Вычислите значение выражения: ,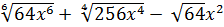

при x = 0,3.

4. Вычислите:

a) 2^-5

b) ( )^-1

c)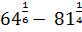

d)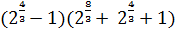

5. Упростите выражение: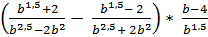

Вариант 2

1. Вычислите:

a)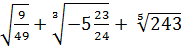

b)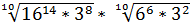

2. Упростите выражение: .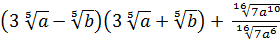

3. Вычислите значение выражения: 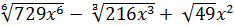, при

x = 2,4.

4. Вычислите:

a) 5^-3

b) ( )^-1

c)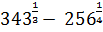

d) .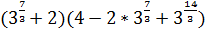

5. Упростите выражение: 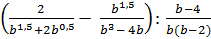.