Буквенная запись свойств вычитания
И сложения (п. 9)
Цели:научить применять свойства сложения и вычитания для упрощения вычислений и буквенных выражений.
Оборудование: плакат «найди пропущенные числа»; кодоскоп, кодопозитивы.
Ход урока
I. Проверка домашнего задания.
1. Воспроизвести на листах таблицу свойств сложения и вычитания.
2. Соседи по парте обмениваются тетрадями, сверяют ответы с доской, исправляют ошибки и ставят оценку друг другу в тетради.
II. Устные упражнения.
1. Придумать задачу, решением которой является выражение: 81 – (х + у).
2. Среди чисел, записанных во втором столбце, найдите ответы:
а) 30462 – 693 1) 1874
б) 2567 – 693 2) 29769
в) 31452 – 693 3) 1875
г) 2568 – 693 4) 30759
3. Плакат: «Найдите пропущенные числа»:
а)
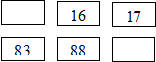
б)
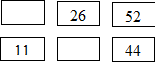
4. По кодоскопу на экране проецируются:
а) б)
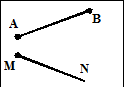
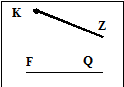
Ответить на вопросы:
Какие фигуры изображены? В чем их сходство? Чем отличаются?
III. Работа по теме урока.
№ 344 (а, в); 348
Самостоятельная работа по вариантам.
Вариант I: № 345 (г); 346 (в); 359.
Вариант II: № 345 (д); 346 (г); 357.
IV. Итог урока.
Выполните вычисления по схеме:
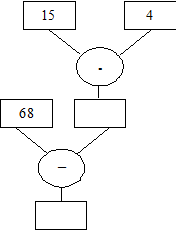
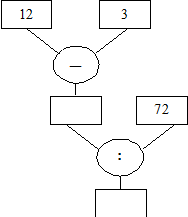
V. Домашнее задание: п. 9, № 364 (в), 365 (б), 369, 371 (б, г).
Урок № 33
Уравнение (п. 10)
Цели:научить формулировать определения уравнения, корня, объяснить, что значит решить уравнение, а также учить решать уравнения.
Оборудование: плакат с рисунками из п. 10; плакат с высказывание М. А. Эйнштейна.
Ход урока
I. Изучение нового материала.
1. Высказывание А. Эйнштейна: «Мне приходится делить свое время между политикой и уравнениями. Однако уравнение, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
2. Рассмотреть решение задачи из п. 10.
3. Равенство может быть верным или неверным.
4. Определения уравнения, корня; что значит решить уравнение (после объяснения учителя ученики читают эти определения по учебнику, запоминают и рассказывают друг другу при сменных парах).
5. Рассмотреть примеры и сформулировать ответы на вопросы: как найти неизвестные слагаемые? Как найти неизвестное уменьшаемое? Вычитаемое?
Примеры: х + 18 = 40; х – 16 = 20; 36 – х = 25.
II. Закрепление.
1. Выполнить: № 372 (а, в, г) – предварительно сформулировать нужное правило; № 374, 373 (а) – показать образец правильного оформления задачи.
Пусть в корзине было х грибов. Так как в корзину положили 27 грибов, то в ней стало (х + 27) грибов, что по условию задачи составляет 75 грибов.
Решение
Составим уравнение: х + 27 = 75.
х = 75 – 27; х = 48.
Итак, в корзине было 48 грибов.
Ответ: 48 грибов.
2. Самостоятельная работа по вариантам:
Вариант I: № 393 (а).
Вариант II: № 393 (г).
III. Итог урока.
Учитель: Что сегодня на уроке узнали нового?
Ответить на вопросы:
1) Какое равенство называется уравнением?
2) Какое число называется корнем уравнения?
3) Что значит решить уравнение?
4) Как проверить, верно ли решено уравнение?
5) Как найти неизвестное слагаемое? вычитаемое? уменьшаемое?
IV. Домашнее задание:п. 10; № 395 (а, в); 398, 403 (а), повторить п. 6. Придумать частушки про уравнения. В математический словарь: уравнение, корень, решить уравнение.
Урок № 34
