Оценки параметров распределения

Одной из задач статистики является оценка параметров распределения случайной величины Х по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 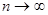, где объем выборки. Для оценки параметров распределения Х из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Обозначим через θ оцениваемый параметр, через - оценку этого параметра. Для того чтобы оценка давала хорошее приближение, она должна удовлетворять определенным требованиям.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру θ, т.е. , в противном случае оценка называется смещенной.

Состоятельной называют статистическую оценку параметра , что для любого наперед заданного числа вероятность при 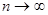стремится к 1.

Это означает, что при достаточно больших можно с вероятностью, близкой к 1, т. е. почти утверждать, что оценка отличается от оцениваемого параметра меньше чем на .

Несмещенная оценка будет состоятельной, если при 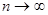её дисперсия стремится к нулю: .

Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии: .

Если варианты - большие числа, то для облегчения вычисления формулу для преобразуют к виду: , где С- ложный нуль.

Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.

При этом, чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценку, обладающую таким свойством, называют эффективной.

Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.

Пусть - оцениваемый параметр, - его оценка, составленная из Х₁, Х₂, …, Х_п.

Если известно, что оценка является несмещенной и состоятельной, то по данным выборки вычисляют значение и считают его приближением истинного значения . При этом среднеквадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называют точечными.

Пусть - некоторое число. Если выполняется неравенство , т. е. , что можно записать в виде , то говорят, что интервал покрывает параметр . Однако невозможно указать оценку , чтобы событие было достоверным, поэтому будем говорить о вероятности этого события. Число называют точностью оценки .

Определение. Надежностью (доверительной вероятностью) оценки параметра для заданного называют вероятность того, что интервал покроет параметр , т.е. .

Определение. Доверительным интерваломназывают найденный по данным выборки интервал(θ^*- δ; θ^* +δ), который полностью покрывает параметр θ с заданной надежностью γ.

Надежность γ обычно принимают равной 0,95, 0,99 или 0,999.

Нельзя категорически утверждать, что найденный доверительный покрывает параметр . Но в этом можно быть уверенным на 95% при , на 99% при и т. д. Это означает, что если сделать много выборок, для 95% из них (если ) вычисленные доверительные интервалы действительно покроют .

В некоторых случаях среднее квадратическое отклонение σ ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения проводятся одним и тем же прибором при одних и тех же условиях, то σ для всех измерений одно и то же и обычно бывает известно.

Пусть случайная величина X распределена нормально с параметрами a и σ, причем σ известно. Построим доверительный интервал, покрывающий неизвестный параметр a с заданной надежностью γ. При этом .

Потребуем, чтобы выполнялось соотношение , где - наперед заданная надежность.

Используя известные формулы получаем, . Так как Р задана и равна , то окончательно имеем: .

Смысл этого соотношения: с надежностью γ можно утверждать, что доверительный интервал покрывает неизвестный параметр a. Точность оценки . Здесь число t определяется из равенства по таблице.

При неизвестном σ (и объеме выборки ) ,где S – исправленное среднее квадратическое отклонение: .

Пусть случайная величина Х имеет нормальное распределение с неизвестными нам параметрами а и . Оказывается, что случайная величина (обозначим её возможные значения через t) , где п-объем выборки, -выборочная средняя, S- исправленное среднее квадратическое отклонение) имеет распределение, не зависящее от а и .Ононазывается распределением Стьюдента.

Плотность вероятности распределения Стьюдента задается формулой: , где коэффициент зависит от объема выборки. Потребуем, чтобы выполнялось соотношение: , где - заданная надежность, приходим к утверждению: с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр а, точность оценки . Здесь случайные величины и S заменены неслучайными величинами 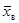и s, найденными по выборке.

При распределение Стьюдента практически не отличается от нормированного нормального распределения.

Для нахождения доверительного интервала для среднего квадратического отклонения σ будем пользоваться следующим предложением:

С надежностью γ можно утверждать, что доверительный интервал покрывает неизвестный параметр σ, точность оценки , где S – исправленное выборочное среднее квадратическое отклонение: ; q - находят по таблице по заданным n и γ.

Причем: если q<1, то ,

если q>1, то .

Пусть проводится п независимых равноточных измерений (измерений проводимых в одинаковых условиях и одним прибором) некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины Х₁, Х₂, …, Х_п. Так как обычно неизвестно, следует пользоваться предложением: с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр а, точность оценки . Здесь случайные величины и S заменены неслучайными величинами 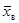и s, найденными по выборке.

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения случайных ошибок измерений. Для оценки используют «исправленное» среднее квадратическое отклонение s. Утверждение: с надежностью γ можно утверждать, что доверительный интервал покрывает неизвестный параметр σ, точность оценки , где S – исправленное выборочное среднее квадратическое отклонение: , применимо для оценки точности измерений.