Амплитудно-фазовая (частотная) характеристика или годограф Найквиста

Амплитудно-фазовая характеристика (годограф Найквиста) - Графическое отображение для всех частот спектра отношений выходного сигнала САУ к входному, представленных в комплексной форме. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка.

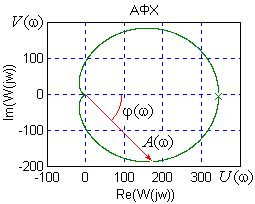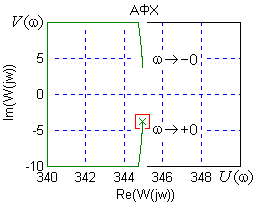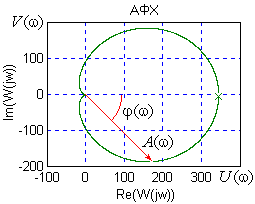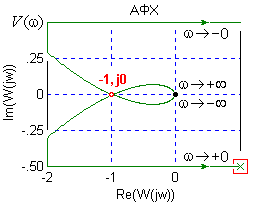
От АФХ порождаются все другие частотные зависимости:

• U(w) - четная (для замкнутых САУ P(w));
• V(w) - нечетная;
• A(w) - четная (АЧХ);
• j(w) - нечетная (ФЧХ);
• ЛАЧХ & ЛФЧХ - используются наиболее часто.

Логарифмические ЧХ - ЛАЧХ & ЛФЧХ

Построение ЛАЧХ & ЛФЧХ производится по выражениям:

L(w) = 20 lg |W(jw)| = 20 lg A(w), [дБ]; j(w) = arg(W(jw)), [рад].

Числитель и знаменатель ПФ САР могут быть представлены либо в виде отношения полиномов:

,

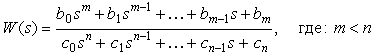либо в виде отношения их разложений на элементарные множители:

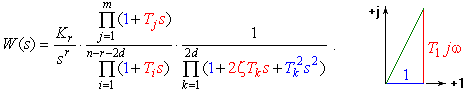(1)

Подстановка sjw позволяет перейти в частотный домен. При наличии ЭВМ построение ЛАЧХ & ЛФЧХ не составит труда в любом случае. Однако разложенная на множители ПФ (1) позволяет построить асимптотические ЛАЧХ & ЛФЧХ практически без вычислительной работы. Каждый линейный множитель ее числителя и знаменателя есть комплексное число. Найдем модуль каждого (как гипотенузу прямоугольного треугольника), и перейдем к логарифмическому масштабу:

.

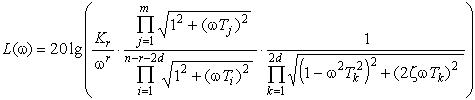Для упрощения дальнейших построений избавимся от операции умножения, заменив ее операцией сложения в логарифмическом домене:

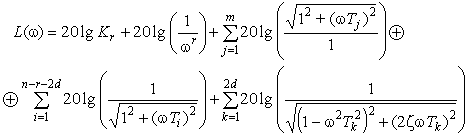(2).

Легко понять, что каждое слагаемое выражения (2) есть либо прямая линия, либо асимптотически приближается к прямым линиям при устремлении частоты к нулю и к бесконечности. Наклон аппроксимирующих прямых всегда кратен 20 дБ за декаду.

Для построения ЛФЧХ необходимо найти фазу каждого множителя числителя и знаменателя частотной ПФ, как арктангенс отношения его противолежащего катета к прилежащему (напомним, что при произведении комплексных чисел (в экспоненциальной форме) фазы (показатели степени) складываются, а при делении - вычитаются). Таким образом, построение ЛФЧХ производится по выражению:

.

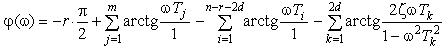Отметим так же, что одному Белу соответствует увеличение мощности в 10 раз. Поскольку A - это физическая величина либо первого, либо второго рода, а не их произведение (т.е. не мощность); увеличение ее в 10 раз соответствует увеличению мощности в 100 раз, что соответствует двум Белам или 20 дБ.

Правила построения асимптотических ЛАЧХ & ЛФЧХ

Правила построения асимптотических ЛАЧХ & ЛФЧХ, точнее каждого слагаемого выражения (2) показаны на рисунках.

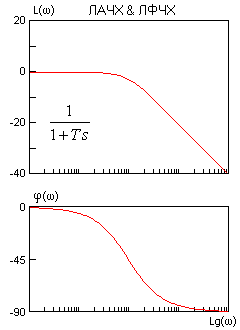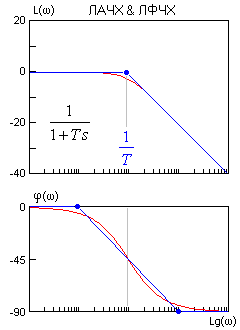
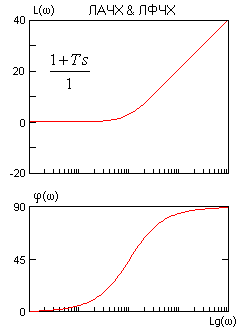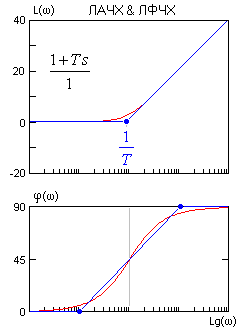
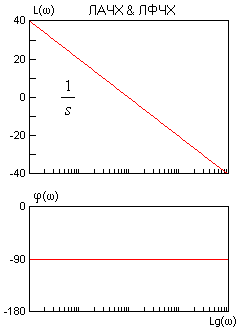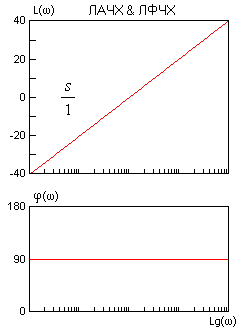
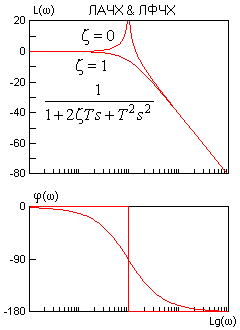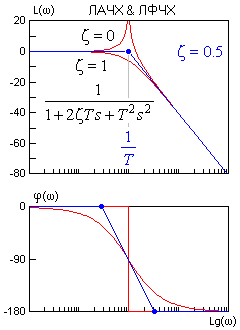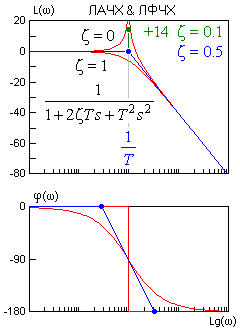
Точность асимптотических ЛАЧХ & ЛФЧХ достаточна в большинстве случаев. Для звеньев первого порядка максимальная амплитудная ошибка вблизи частоты сопряжения составляет 3 дБ. Максимальная фазовая ошибка - 6%. Фрагмент ЧХ колебательного звена вблизи резонансной частоты лишь иногда следует уточнить по опорным справочным кривым для данного z.