Изображение периодических функций

Пусть f(t) – периодическая функция периода T. Обозначим f₀(t) один первый период этой функции, т. е.

(*)

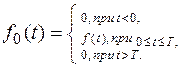Пусть .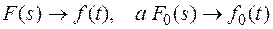

Равенство (*) можно рассматривать как импульс и для определения изображения этого импульса можно воспользоваться равенством (1) предыдущего параграфа.

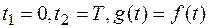
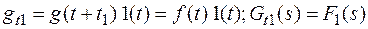
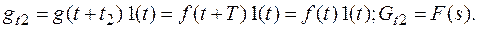
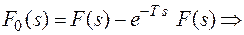
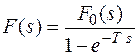
Это равенство позволяет найти изображение периодической функции по изображению одного первого периода этой функции.

ЛЕКЦИЯ 15

План лекции

1. Решетчатые функции.

2. Конечная разность, конечная сумма.

3. Разностные уравнения.

4. Линейные разностные уравнения.

РЕШЕТЧАТЫЕ ФУНКЦИИ.

D- И Z- ПРЕОБРАЗОВАНИЯ.

Решетчатые функции.

Наряду с функциями f(t), заданными в каждой точке числовой оси t, рассмотрим функции, заданные лишь в некоторых точках Такие функции называются решетчатыми. Обычно решетчатые функции задают в равноотстоящих точках t = nT, где n – любое целое число, T = const, называемая периодом дискретности.

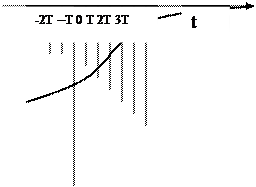Каждой функции f(t) непрерывного аргумента t соответствует бесконечное множество решетчатых функций, для этого достаточно положить, что

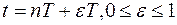. Функция 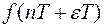при фиксированном 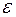также является решетчатой, и называется смещенной.

Строго говоря, решетчатые функции являются функциями аргумента n, где n пробегает 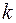значений целых чисел, поэтому решетчатая функция обозначается также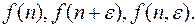

Для решетчатой функции вводятся понятия конечная разность, конечная сумма, которые в некотором смысле аналогичны понятиям интеграла и производной для обычных функций.

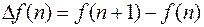- называется конечной разностью 1-го порядка функции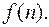

Конечной разностью 2-го порядка функции 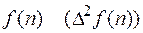называется конечной разностью 1-го порядка функции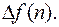

.

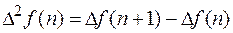Аналогично, конечной разностью 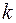- го порядка функции 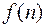называется

.

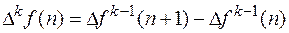Конечную разность любого порядка можно определить через значение функции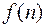

.

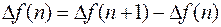
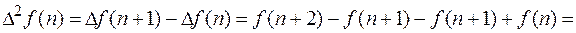
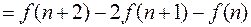
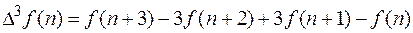Справедлива формула

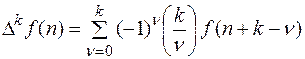
здесь 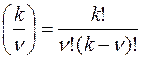- число сочетаний.

Функция F(n) называется первообразной функции f(n), если конечная разность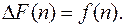

В дальнейшем будем рассматривать решетчатые функции f(n), определяемые только для положительных n = 0,1,2,… . Для таких n

.

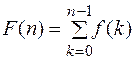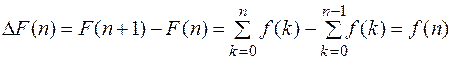
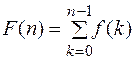- конечная сумма.

Разностные уравнения.

Уравнение вида

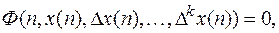(1)

связывающее решетчатую функцию x(n) и ее конечные разности, называется разностным уравнением.

Это уравнение с помощью формулы

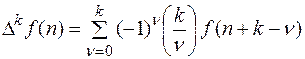
можно привести к виду, в котором содержатся только решетчатые функции x(n)

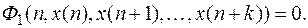(2)

Например, уравнение

.

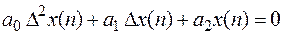
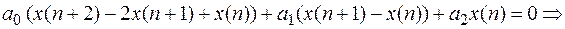
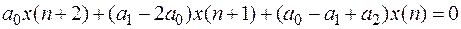Если в уравнении (2) одновременно присутствуют функци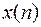и и 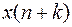, то говорят, что уравнение (1) имеет порядок k. При переходе от (1) к (2) функция 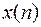может сократиться, т. е. (2) может иметь вид

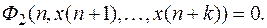(3)

Введем 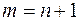, тогда

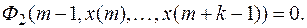(4)

В этом случае уравнение (1) имеет порядок (k – 1). В литературе разностные уравнения обычно изучаются в форме (2).

Решетчатая функция x(n), обращающая уравнение (2) в тождество, называется решением этого уравнения.