Методика работы с правилами и алгоритмами

Понятие «алгоритм» является основным, неопределяемым. Его сущность заключается в предписании, указывающем, какие операции и в какой последовательности надо выполнить с данными, чтобы решить любую задачу данного типа. Характеристические свойства понятия «алгоритм»: а) массовость (с помощью данного алгоритма могут быть решены все задачи определенного типа); б) дискретность шагов (при построении алгоритма выделены отдельные и законченные операции); в) элементарность шагов (каждую выделенную операцию в состоянии выполнить исполнитель алгоритма); г) результативность (точное выполнение указаний алгоритма при решении любой задачи из данного класса однотипных задач всегда должно приводить к определенному результату).

Правило представляет собой свернутый алгоритм: некоторые его шаги являются системами операций в сжатом виде, а отдельные операции, необходимые на начальном этапе формирования метода, вообще не содержатся в формулировке правила. Правила выражаются формулами и словесными формулировками.

Цель использования алгоритмов и правил – формирование общих методов решения класса однотипных задач.

Основные этапы работы с правилами и алгоритмами в школе:

– введение алгоритма (цель – актуализация знаний, необходимых для введения и обоснования алгоритма, а также формирование алгоритма);

– усвоение алгоритма (цель – отработка операций, входящих в алгоритм, и усвоение их последовательности);

– применение алгоритма (цель – отработка алгоритма в знакомых и незнакомых ситуациях).

При изучении особенными школьниками правил и алгоритмов необходимо учитывать замедленный темп формирования обобщенных знаний, интеллектуальную пассивность детей, повышенную утомляемость их в процессе интеллектуальной деятельности.

Оптимальным для этой категории школьников является изучение правил в несколько замедленном темпе, с более широкой наглядной и словесной конкретизацией общих положений, с большим количеством тренировочных упражнений.

При работе над правилами с особенными детьми эффективно использование различных памяток-инструкций, которые позволяют осуществить коррекцию недостатков их памяти и мышления. Проговаривая и выполняя инструкцию по отдельным этапам, дети учатся правильно рассуждать и контролировать себя в процессе самостоятельной работы. Например, при умножении на круглые десятки и сотни отдельным ученикам будет полезна памятка следующего содержания:

1. Подпиши множители один под другим так, чтобы нули остались в стороне.

2. Выполни умножение, не обращая внимание на нули.

3. Сосчитай число нулей в обоих множителях и припиши эти нули к произведению.

Важно предусмотреть постепенное сокращение помощи со стороны и такое же постепенное увеличение трудности предлагаемых заданий. Серьезное внимание следует уделить мотивационно-занимательной стороне обучения, стимулирующей развитие познавательных интересов.

В качестве примера рассмотрим работу учителя с особенными учащимися над правилом сравнения обыкновенных дробей с одинаковыми знаменателями.

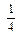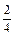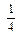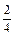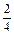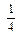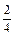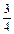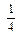Со сравнением дробей можно познакомить учащихся, широко используя их знания и опыт в получении дробей путем деления целого предмета (единицы) на равные части. Берем яблоко, делим его на четыре равные доли. Сравним долю яблока и . Что больше: или ? Учащиеся наглядно убеждаются, что больше . Так же сравниваются и ; и 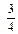. Учитель обращает внимание на знаменатели и числители сравниваемых дробей. Учащиеся, наблюдая, убеждаются, что среди дробей с одинаковыми знаменателями дробь с большим числителем оказывается большей.

Затем учитель пишет ряд дробей 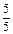; ; 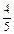; ; 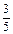; 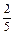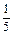с одинаковыми знаменателями, но разными числителями и просит рассказать и показать, как получить эти дроби, используя полоски бумаги или отрезки. Он обращает внимание учащихся сначала на знаменатели всех записанных дробей (знаменатели всех дробей одинаковые), а затем на их числители (числители разные) и с помощью чертежа просит сравнить эти дроби. Так учащиеся подводятся к обобщению, что при одинаковых знаменателях та дробь больше, у которой чис­литель больше. Для вывода правила необходимо рассмотреть (на круге, дробных счетах, квадрате) еще ряд дробей с одинаковыми знаменателями, но разными числителями и сравнить их.

Такие упражнения позволят учащимся сознательно усвоить правило сравнения дробей с одинаковыми знаменателями. Во всех случаях следует подчеркивать и останавливать внимание учащихся на том, что доли, которые сравниваются, одинаковые, но количество этих долей разное. Следовательно, чем больше долей, тем дробь больше. 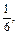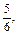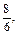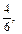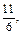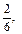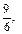Далее учащимся можно предлагать задания более отвлеченного характера, например такие: сравнить следующие дроби: 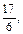записать их от меньшей к большей (и наоборот); назвать наименьшую (наибольшую) дробь из данного ряда дробей; назвать из данного ряда дробей дроби меньше 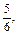(больше ).

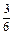Чтобы предупредить формальное усвоение учащимися знаний по этой теме, механическое использование правила сравнения дро­бей, необходимо время от времени требовать от учащихся изобра­жения и сравнения дробей на рисунках.

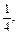
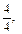
Целесообразно также научить учащихся сравнивать дроби с единицей и на основе этих знаний, ориентируясь на «зону ближайшего развития ребенка», дать понятие о правильной и неправильной дроби. Например, стоит выполнить задание: показать дроби 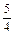на отрезках, полосках, кругах; ответить на вопрос, какие из дробей меньше единицы, какие равны 1, какие больше 1.