Графический метод решения задач линейного программирования
Наиболее простым и наглядным методом решения задачи линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.
Рассмотрим задачу ЛП в стандартной форме записи:
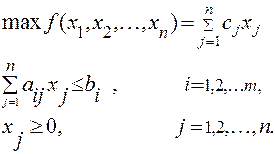
Положим n=2, т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ai1 x1 + ai2 x2 = bi , i=1,2,…m. Условия неотрицательности определяют полуплоскости, соответственно, с граничными прямыми x1=0,x2 =0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х1+3х2£ 12. Во-первых, построим прямую 2х1+3х2=12. Эта прямая проходит через точки (6, 0) и (0, 4). Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет
неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим х1=х2=0 в неравенство 2х1+3х2£12. Получим 2´0+3´0£12. Данное утверждение является верным, следовательно, неравенству 2х1+3х2£12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на рис.1.
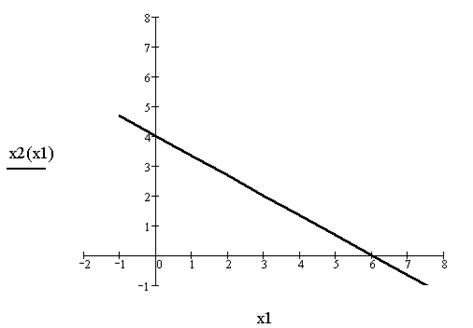 |
Рис. 1. Неравенству 2х1+3х2£12 соответствует нижняя полуплоскость.
Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет условиям неотрицательности (xj ³0, j=1,…,n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т.е.
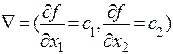 .
.
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая 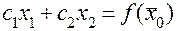 , перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.
, перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – убывает.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Графический метод решения ЗЛП состоит из следующих этапов.
1. Строится многоугольная область допустимых решений ЗЛП – ОДР,
2. Строится вектор-градиент ЦФ в какой-нибудь точке Х0 принадлежащей ОДР –
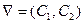 .
.
3. Линия уровня C1x1+C2x2 = а (а–постоянная величина) - прямая, перпендикулярная вектору –градиенту 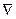 – передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
– передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,x2), найденное в получаемой точке, является максимальным.
При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1,x2) не существует.
Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
Рассмотрим графическое решение задач линейного программирования на следующем примере.
Задача. о планировании выпуска продукции пошивочному предприятию.
Намечается выпуск двух видов костюмов - мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм - 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Tребуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского - 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.
Модель задачи.
Введем следующие обозначения: х1 - число женских костюмов; x2 - число мужских костюмов.
Прибыль от реализации женских костюмов составляет 10х1, а от реализации мужских 20х2, т.е. необходимо максимизировать целевую функцию
f(x) = 10´ х1 + 20´ х2 -> max.
Ограничения задачи имеют вид:
х1 + х2 £ 150
2 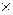 х1 + 0.5
х1 + 0.5 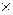 х2 £ 240
х2 £ 240
х1 + 3.5 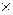 х2 £ 350
х2 £ 350
х2³ 60
х1 ³ 0
Первое ограничение по труду х1 + х2 £ 150. Прямая х1 + х2 = 150 проходит через точки (150, 0) и (0, 150).
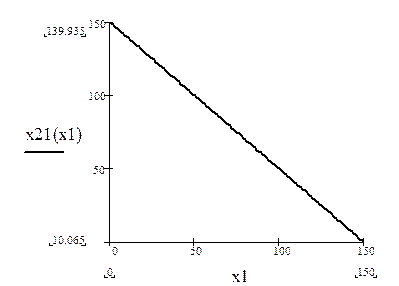
Рис. 2. Решением первого неравенства является нижняя полуплоскость.
Второе ограничение по лавсану 2 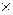 х1 + 0.5
х1 + 0.5 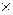 х2 £ 240. Прямая 2
х2 £ 240. Прямая 2 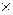 х1 + 0.5
х1 + 0.5 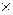 х2 = 240 проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х1 + 3.5
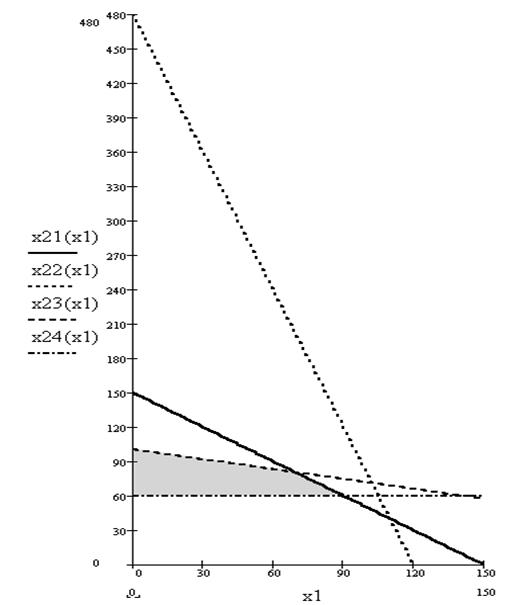
х2 = 240 проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х1 + 3.5 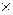 х2 £ 350. Добавим четвертое ограничение по количеству мужских костюмов х2 ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60. На рис.3. заштрихована область допустимых решений.
х2 £ 350. Добавим четвертое ограничение по количеству мужских костюмов х2 ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60. На рис.3. заштрихована область допустимых решений.
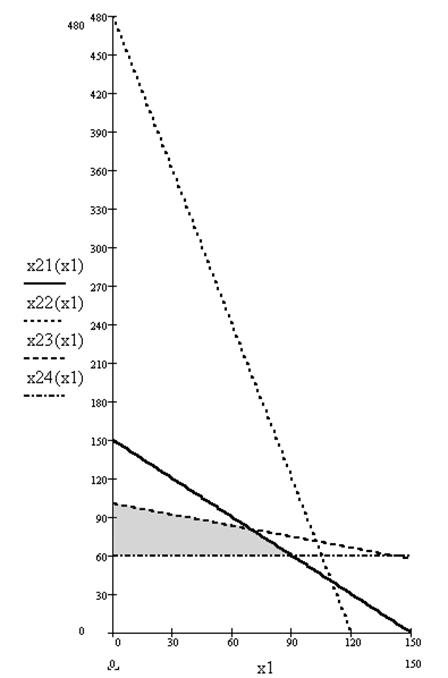
Рис. 3. Заштрихована область допустимых решений.
Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е. 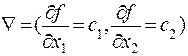 = (10;20).
= (10;20).
Что бы построить этот вектор, нужно соединить точку (10;20) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации — в противоположном направлении. Для удобства можно строить вектор, пропорциональный вектору Ñ. Так, на рис. 2.1.6. изображен вектор градиент (30;60).
В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:
х1 + 3.5 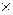 х2 = 350
х2 = 350
х1 + х2 = 150 .
Отсюда легко записать решение исходной ЗЛП: max f(x) = 2300 и достигается при x1=70 и x2=80 (рис. 4.)
Рис.4. Максимум целевой функции достигается в точке (70, 80).
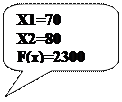 |
Задача.Для изготовления двух видов продукции А1 и А2 используют три вида ресурсов S1, S2, S3, запасы которых составляют 18, 16 и 5 усл.ед. Расход ресурсов на 1 ед. продукции приведен в таблице:
| Виды ресурсов | Запасы ресурсов | Расходы ресурсов на 1 изд. | |
| А1 | А2 | ||
| S1 | 18 | 1 | 3 |
| S2 | 16 | 2 | 1 |
| S3 | 5 | - | 1 |
| Прибыль | 2 руб. | 3 руб. |
Необходимо составить такой план производства продукции, который обеспечит наибольшую прибыль от ее реализации.
Составим экономико-математическую модель (ЭММ) задачи.
Пусть надо выпустить изделий A1 - x1 шт., а изделий А2 - x2 шт. Тогда прибыль F = 2x1 + 3x2 Þ max
 x1 + 3x2 £ x1 + 3x2 £ | 18 |
| 2x1 + x2 £ | 16 |
| x2 £ | 5 |
| x1 ³ 0, | x2 ³ 0 |
Решим задачу графически.
| 1) | x1 + 3x2 £ 18 | ||
| x1 + 3x2 = 18 (0; 6) (18; 0) | |||
| к.т. (0; 0), 0 + 3*0 < 18 (в) – входит | |||
| 2) | 2x1 + x2 £ 16 | ||
| 2x1 + x2 = 16 (0; 16) (8; 0) | |||
| к.т. (0; 0), 2*0 + 0 < 16 (в) – входит | |||
| 3) | x2 £ 5 | ||
| x2 = 5, x2 < 5 - ниже прямой | |||
| 4) | x1 ³ 0 - правее ОX2 | ||
| 5) | x2 ³ 0 - выше ОX1 | ||
| Линия уровня | F = 2x1 + 3 x2 F = 0 | ||
| 2x1 + 3x2 = 0 (0; 0) (3; -2) | |||
 | q = {2; 3} - указывает направление возрастания F. | ||
max F достигается в т. С
| т.С | x1 + 3 x2 = 18 | Þ - | 2 x1 + 6 x2 = 36 | Þ | 5 x2 = 20 | Þ |
| 2x1 + x2 = 16 | 2 x1 + x2 = 16 | x1 + 3 x2 = 18 | ||||
| Þ | x2 = 4 | |||||
| x1 = 6 |
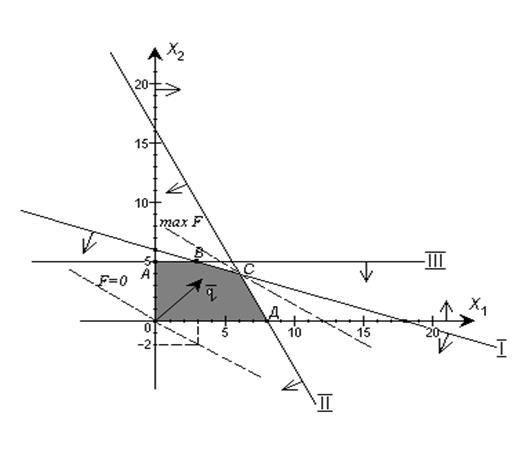 |
Таким образом, необходимо выпустить x1 = 6 шт. изделий А1, x2 = 4 шт. изделий А2, чтобы получить max F = 2*6 + 3*4 = 24 ден.ед.
