Прохождение случайных сигналов через линейные системы

Существует два подхода к исследованию систем управления при случайных возмущениях:

1) вероятностный – на основе плотностей распределения вероятностей;

2) статистический – с помощью усредненных характеристик: математического ожидания, дисперсии, корреляционной функции, спектральной плотности.

Применение вероятностного подхода, как правило, связано со значительными трудностями. С одной стороны, они вызваны недостатком информации о плотностях распределения случайных сигналов. С другой стороны, существующий математический аппарат достаточно сложен. Приведем только один важный факт: если входной сигнал имеет нормальное распределение, то на выходе линейной системы будет также сигнал с нормальным распределением.

В прикладных задачах нас чаще всего интересует не плотность распределения вероятностей на выходе системы, а некоторые более осязаемые характеристики – среднее значение, дисперсия и т.д. Поэтому в подавляющем большинстве случаев используется статистический подход. Далее мы будем предполагать, что на вход линейной системы с известной передаточной функцией действует стационарный случайный процесс с заданной спектральной плотностью .

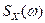Прежде всего, отметим, что при стационарном случайном входе выход линейной системы – тоже стационарный случайный процесс (линейная система его не «портит»). Для процесса требуется найти

· математическое ожидание ;

· дисперсию ;

· корреляционную функцию ;

· спектральную плотность .

Проще всего решается вопрос с математическим ожиданием: среднее значение выхода равно среднему значению входа, умноженному на статический коэффициент усиления системы (коэффициент усиления постоянного сигнала):

.

Учитывая, что в линейных системах справедлив принцип суперпозиции (реакция на сумму двух сигналов равна сумме реакций на отдельные сигналы), далее мы для простоты будем рассматривать только центрированные процессы, имеющие нулевые средние значения.

Остальные характеристики удобнее определять с помощью спектральной плотности выхода. Вспомним, что спектральная плотность – это плотность распределения мощности сигнала по частотам. Сначала рассмотрим, как изменяется мощность гармонического сигнала , когда он проходит через линейную систему. Из классической теории автоматического управления известно, что на выходе устанавливается гармонический процесс с той же частотой, но с другой амплитудой и фазой:

,

причем его амплитуда определяется по частотной характеристике :

.

Мощность гармонического сигнала (средний квадрат) пропорциональна квадрату амплитуды:

.

В последнем равенстве использовано свойство комплексного числа – квадрат его модуля равен произведению этого числа на комплексно-сопряженное, то есть на .

Таким образом, мы с помощью простых рассуждений вышли на очень важный результат: при гармоническом входе с частотой мощность сигнала на выходе линейной системы равна мощности входного сигнала, умноженной на . Учитывая, что это свойство справедливо на всех частотах, и заменив слово «мощность» на «спектральную плотность», получаем формулу, позволяющую сразу найти спектр процесса на выходе:

.

Соответствующая корреляционная функция может быть найдена как обратное преобразование Фурье от . Для вычисление среднего квадрата процесса нужно проинтегрировать :

.

Если процесс центрированный, средний квадрат совпадает с дисперсией, то есть . В общем случае для вычисления дисперсии нужно использовать равенство .

Выделим один важный случай, когда входной сигнал – это единичный белый шум с постоянной спектральной плотностью (белый шум единичной интенсивности). Тогда получаем

.

(6)

Таким образом, спектральная плотность выхода системы, на вход которой действует единичный белый шум, равна квадрату ее амплитудной характеристики.

Пусть передаточная функция линейной системы равна . Белый шум, проходя через такое звено, превращается в сигнал, имеющий спектральную плотность

,

график которой показан на рисунке:

Белый шум «содержит» все частоты, но они по-разному преобразуются. Постоянный сигнал (имеющий частоту ) передается на выход системы без изменений. На низких частотах искажения достаточно малые, а высокие частоты подавляются (фильтруются) системой. Это типичный фильтр низких частот (он пропускает низкочастотные сигналы и блокирует высокочастотные). Отметим очень важный факт: поскольку высокие частоты подавляются, отклонения спектра входного сигнала от равномерного спектра белого шума в этой области не будут существенно влиять на спектр выхода. На этой идее основано компьютерное моделирование случайных процессов (см. далее).