Анализ случайных процессов в Matlab

Чтобы вычислить дисперсию и СКВО случайного процесса, значения которого записаны в массив x, применяются функции var и std:

v = var(x); % дисперсия

sigma = std(x); % среднеквадратическое отклонение

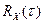Для анализа корреляционной функции удобно использовать функции пакета Signal Processing Toolbox (обработка сигналов). Функция xcorr вычисляет двустороннюю корреляционную функцию . Для того, чтобы получить правильные абсолютные значения корреляционной функции, результат нужно разделить на количество отсчетов исходного сигнала. Например, если значения сигнала находятся в массиве x, корреляционная функция может быть вычислена так:

R = xcorr(x) / length(x);

Если построить ее мы получим значения как для положительных, так и для отрицательных 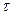. Если нужны только значения при , первую часть приходится «обрезать», учитывая, что график симметричный.

Rplus = R(floor(length(R)/2):end);

Здесь функция length вычисляет длину массива, а floor – округляет результат в меньшую сторону.

Для оценки спектра в заданном частотном диапазоне, например, рад/с, можно использовать два подхода. Метод Блэкмана-Тьюки использует преобразование Фурье корреляционной функции:

w = [0:0.1:5];

Sw = [];

for i=1:length(w)

Sw(i) = sum(Rplus .* cos(w(i)*t));

end;

Sw = 2*T*Sw;

Здесь в массиве t записано время, соответствующее отсчетам оценки корреляционной функции Rplus для положительных 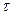, а T – это интервал между этими отсчетами. Операция .* (точка и знак умножения) обозначает поэлементное умножение массивов одного размера.

При использовании окна нужно предварительно умножить корреляционную функцию на весовые коэффициенты. Например, для окна Хэмминга

hamm = 0.54 + 0.46*cos(pi*t/max(t));

Rplus = Rplus .* hamm;

Потом выполняется программа оценки спектра, приведенная выше.

Второй метод использует дискретное преобразование Фурье для исходного сигнала.

N = 512; % число точек (степень двойки)

w = 2*pi*[0:N/2] / N / T; % сетка угловых частот

Fw = T * fft(x, N); % оценка F_X(w)

Sw = Fw .* conj(Fw) / N / T; % оценка S_X(w)

Sw = Sw(1:N/2+1); % взяли первую половину

% до частоты Найквиста

Иногда требуется обеспечить заданный шаг по частоте. Для этого нужно соответствующим образом выбрать 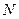, учитывая, что . Отсюда получаем . Это значение нужно округлить «вверх» до ближайшей степени двойки – это можно сделать с помощью функции nextpow2, которая вычисляет ближайшую степень двойки, которая больше заданного числа. В программе это выглядит так (для рад/с):

dw = 0.5; % шаг по частоте

N = 2*pi / dw / T; % количество точек в ДПФ

N = 2^nextpow2(N); % привели к степени двойки

При использовании спектрального окна нужно предварительно умножить исходный сигнал на весовые коэффициенты. При этом для сохранения энергии сигнала учитывается масштабный коэффициент для конкретного окна. Например, для окна Хэмминга

hamm = hamming(length(x));

scale = 1 / sqrt(0.54^2 + 0.46^2/2);

hamm = hamm * scale;

Здесь для построения окна используется функция hamming из пакета Signal Porcessing Toolbox, при вызове которой в скобках указывают количество отсчетов сигнала. Далее ДПФ выполняется для взвешенного сигнала

Fw = T * fft(x.*hamm, N); % оценка F_X(w)

остальные команды в программе не меняются.

[1] Иначе говоря, синусоиду нужно измерять более 2 раз за период.

[2] Можно доказать, что , где звездочка обозначает комплексно-сопряженную величину.