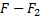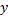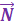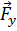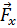Пример применения законов Ньютона
Урок 6. Динамика. Законы Ньютона.
Механическое движение подчиняется основным законам механики – законам Ньютона. Законы Ньютона выполняются только в инерциальных системах отсчета.
Инерция – явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения (т.е. в таких случаях отсутствует ускорение).
 Инерциальные системы отсчета - системы отсчета, относительно которых наблюдается инерция, а также те, которые движутся равномерно и прямолинейно относительно ИСО. (ИСО – системы, ускорение которых равно нулю).
Инерциальные системы отсчета - системы отсчета, относительно которых наблюдается инерция, а также те, которые движутся равномерно и прямолинейно относительно ИСО. (ИСО – системы, ускорение которых равно нулю).
 Первый закон Ньютона:
Первый закон Ньютона:
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действия скомпенсированы.
 Иными словами, если равнодействующая всех приложенных к телу сил равна нулю, то скорость тела остается постоянной.
Иными словами, если равнодействующая всех приложенных к телу сил равна нулю, то скорость тела остается постоянной.
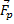 = 0 → v = const
= 0 → v = const
|
 Равнодействующей силой называется векторная сумма всех приложенных к телу сил (см. мат. справку «Векторная сумма» в уроке 3).
Равнодействующей силой называется векторная сумма всех приложенных к телу сил (см. мат. справку «Векторная сумма» в уроке 3).  Второй закон Ньютона:
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
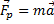
Заметка: Направление ускорения, всегда совпадает с направлением равнодействующей силы, т.к. m>0.
 Третий закон Ньютона:
Третий закон Ньютона:

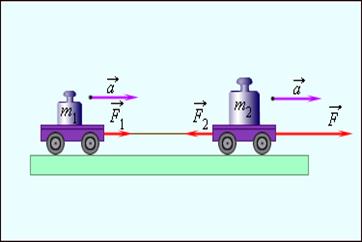
 Тела действуют друг на друга с силами, направленными вдоль одной прямой, противоположными по направлению и равными по модулю.
Тела действуют друг на друга с силами, направленными вдоль одной прямой, противоположными по направлению и равными по модулю.
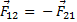
Здесь: 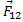 – сила, действующая на первое тело, со стороны второго,
– сила, действующая на первое тело, со стороны второго, 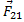 – сила, действующая на второе тело, со стороны первого. Эти силы не компенсируют друг друга, так как они приложены к разным телам!
– сила, действующая на второе тело, со стороны первого. Эти силы не компенсируют друг друга, так как они приложены к разным телам!
 Четвертый закон Ньютона (Закон всемирного тяготения):
Четвертый закон Ньютона (Закон всемирного тяготения):
 Две материальные точки притягиваются друг к другу с силой (силой тяготения), прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Две материальные точки притягиваются друг к другу с силой (силой тяготения), прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
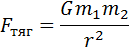
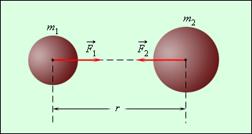 Здесь: G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная, m1 и m2 - массы притягивающихся друг к другу тел (кг), r – расстояние между их центрами масс (м)
Здесь: G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная, m1 и m2 - массы притягивающихся друг к другу тел (кг), r – расстояние между их центрами масс (м)
Силы тяготения направлены вдоль прямой соединяющей центры масс тел.
Пример применения законов Ньютона
|
|
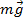 (всегда направленная вниз), сила реакции опоры
(всегда направленная вниз), сила реакции опоры 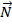 (всегда направлена перпендикулярно поверхности, которой касается тело), сила трения
(всегда направлена перпендикулярно поверхности, которой касается тело), сила трения 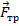 (всегда направлена противоположно движению) и сила тяги
(всегда направлена противоположно движению) и сила тяги 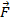 (она заставляет автомобиль двигаться и направлена по направлению движения автомобиля).
(она заставляет автомобиль двигаться и направлена по направлению движения автомобиля). 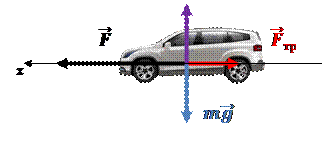 |

По вертикали автомобиль не движется, значит по первому закону Ньютона, равнодействующая всех сил приложенных телу ( по вертикали) равна 0., т.е:
Ох: 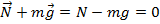 , отсюда следует, что N =mg
, отсюда следует, что N =mg
По горизонтали автомобиль движется равноускоренно, значит по второму закону Ньютона сумма всех приложенных сил (по горизонтали) равна 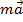
Oy: 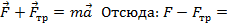 ma.
ma.
Получаем систему уравнений для данного случая:

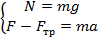
 Математическая справка «Проекции вектора на координатные оси»
Математическая справка «Проекции вектора на координатные оси» 
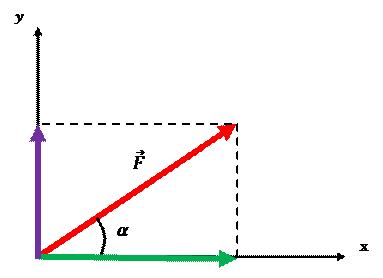
Пусть имеется вектор 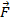 , расположенный под углом α к горизонтали (см. рисунок). Необходимо построить его проекции на координатные оси Ох и Оу.
, расположенный под углом α к горизонтали (см. рисунок). Необходимо построить его проекции на координатные оси Ох и Оу.
Для начала опускаем перпендикуляры из конца вектора на координатные оси Ох и Оу (на рисунке штриховые линии). Затем строим проекции:
Проекция на ось Ох получится если провести вектор из начала вектора 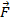 в точку, в которую был опущен перпендикуляр (зеленая стрелка). Проекцию на ось Оу строим аналогично (фиолетовая стрелка:
в точку, в которую был опущен перпендикуляр (зеленая стрелка). Проекцию на ось Оу строим аналогично (фиолетовая стрелка:
Найти модуль этих проекций можно по формулам: (Формулы получаются из прямоугольного треугольника с катетами 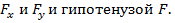 )
)
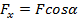 (прилежащий катет)
(прилежащий катет)
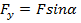 (противолежащий катет)
(противолежащий катет)
| |||||||
| |||||||
| |||||||
 |

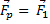 Для m2:
Для m2: 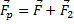 =
=