Дать краткое определение характеристического уравнения. Раскрыть принцип определения типа переходного процесса по типу корней характеристического уравнения
1. Δ=0 характеристическое уравнение где Δ(дельта)-определитель системы уравнений относительно свободных токов, число уравнений равно количеству неизвестных свободных токов.
Составленное по 2ому закону Кирхгофа уравнение :
UL+r*i=E эквивалентно L*(di/dt)+r*i=E
Решение i=iпр(принужденное )+iсв(свободное)
Частное решение = E/R (iпр)
Общим решением этого уравнение является показательная функция следующего вида: A*e^(p*t)
iсв (i свободное ) = A*e^(p*t)
L*(diсв/dt)+r*iсв=0 (приравниваем правую часть к нулю для нахождения свободных токов)
постоянная интегрирования(коэффициент амплитуды) А для каждого свободного тока своя.
а коэффициент затухания(корень характеристического уравнения) р одинаков для свободных токов ветвей
А и р не зависят от времени
А= -(E/r)
P= - (L/r)
Следовательно
i=iпр(принужденное )+iсв(свободное)
i=E/r-(E/r)*e^(-(r/L)*t)
. 


Вопрос13
-основные определения операторного метода нахождения переходных процессов. Объяснить, почему начальные условия учитываются в виде отдельных элементов на эквивалентной операторной схеме
Ответ:Перехо́дныепроце́ссы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, то есть, — при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Операторный метод — это метод расчёта переходных процессов в электрических цепях, основанный на переносе расчёта переходного процесса из области функций действительной переменной (времени t) в область функций комплексного переменного (либо операторной переменной), в которой дифференциальные уравнения преобразуются в алгебраические.
Найдём изображения каждого из слагаемых дифференциального уравнения:
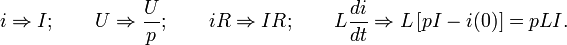 [1]
[1]
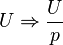 получается потому, что изменение U во времени выражается функцией U = H(t)U (ключ замкнули в момент t = 0), где H(t) — ступенчатая функция Хевисайда, (H(t) = 0 при t < 0 и H(t) = 1 при t = 0 и t > 0, причём изображение H(t) есть 1/p).
получается потому, что изменение U во времени выражается функцией U = H(t)U (ключ замкнули в момент t = 0), где H(t) — ступенчатая функция Хевисайда, (H(t) = 0 при t < 0 и H(t) = 1 при t = 0 и t > 0, причём изображение H(t) есть 1/p).
Получаем следующее изображение дифференциального уравнения
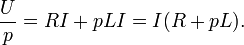
Из последнего выражения найдём изображение тока:
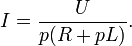
Таким образом, решение сводится к нахождению оригинала тока по известному изображению. Разложим правую часть уравнения на элементарные дроби:
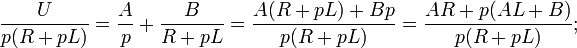
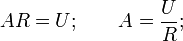
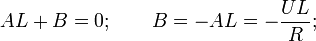
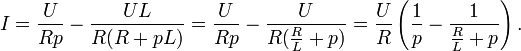
Найдём оригиналы элементов последнего выражения:
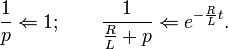
Окончательно получаем
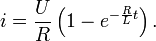
Вопрос14
- объяснить суть подхода к решению методом интеграла Дюамеля. Дать определение переходной проводимости, переходной функции и их роли в нахождении переходного процесса (как учитываются скачки входного напряжения в решении).
Ответ: Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 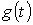 или (и) переходную функцию по напряжению
или (и) переходную функцию по напряжению 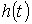 , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
, можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 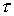 , а вторую - как t.
, а вторую - как t.
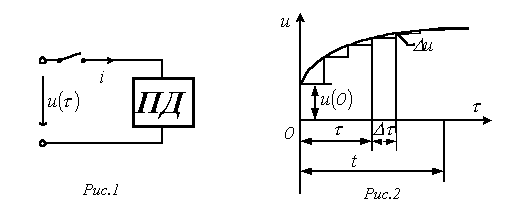
Пусть в момент времени 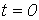 к цепи с нулевыми начальными условиями (пассивному двухполюснику ПДна рис. 1) подключается источник с напряжением
к цепи с нулевыми начальными условиями (пассивному двухполюснику ПДна рис. 1) подключается источник с напряжением 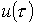 произвольной формы. Для нахождения тока
произвольной формы. Для нахождения тока 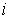 в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения
в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения 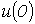 и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.
и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.
В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 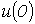 , равна
, равна 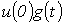 .
.
В момент времени 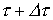 имеет место скачок напряжения
имеет место скачок напряжения 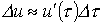 , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока
, который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока 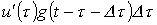 .
.
Полный ток 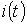 в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом
в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом 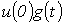 , т.е.
, т.е.
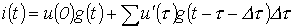 .
.
Заменяя конечный интервал приращения времени 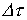 на бесконечно малый, т.е. переходя от суммы к интегралу, запишем
на бесконечно малый, т.е. переходя от суммы к интегралу, запишем
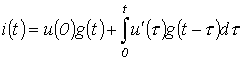 . . | (1) |
Соотношение (1) называется интегралом Дюамеля.
