Модель Лотке-Вольтерра (хищник-жертва)

Математическое моделирование биологических процессов началось с создания первых простейших моделей экологической системы.

Допустим, в некотором замкнутом районе живут рыси и зайцы. Рыси питаются только зайцами, а зайцы – растительной пищей, имеющейся в неограниченном количестве. Необходимо найти макроскопические характеристики, описывающие популяции. Такими характеристиками являются число особей в популяциях.

Простейшая модель взаимоотношений популяций хищника и жертвы, основанная на логистическом уравнении роста, названа (как и модель межвидовой конкуренции) по имени ее создателей - Лотки и Вольтерра. Эта модель крайне упрощает исследуемую ситуацию, но все же полезна в качестве отправной точки в анализе системы хищник-жертва.

Предположим, что (1) популяция жертвы существует в идеальной (независимой от плотности) среде, где ее рост может ограничивать только наличие хищника, (2) столь же идеальна среда, в которой существует хищник, рост популяции которого ограничивает лишь обилие жертв, (3) обе популяции размножаются непрерывно согласно экспоненциальному уравнению роста, (4) скорость поедания жертв хищниками пропорциональ­на частоте встреч между ними, которая, в свою очередь, является функцией плотности популяций. Эти допущения и лежат в основе модели Лотки - Вольтерра.

Пусть в отсутствие хищников популяция жертвы растет экспоненциаль­но:

dN/dt =r₁N₁

где N -численность, а r, - удельная мгновенная скорость роста популя­ции жертвы. Если же хищники присутствуют, то они уничтожают особей жертвы со скоростью, которая определяется, во-первых, частотой встреч хищников и жертв, возрастающей по мере увеличения их численностей, и, во-вторых, эффективностью, с которой хищник обнаруживает и ловит свою жертву при встрече. Число жертв, встреченных и съеденных одним хищником N_с, пропорционально эффективности охоты, которую мы выразим через коэффициент С_1; численности (плотности) жертвы N и времени, затраченному на поиски Т:

N_C=C₁NT (1)

Из этого выражения легко определить удельную скорость потребления жертв хищником (т.е. число жертв, поедаемых одной особью хищника в единицу времени), которую часто называют также функциональным ответом хищника на плотность популяции жертвы:

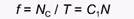(2)

В рассматриваемой модели С₁ является константой. Это означает, что число жертв, изъятых хищниками из популяции, линейно возрастает с увеличением ее плотности (так называемый функциональный ответ типа 1). Ясно, что общая скорость поедания жертв всеми особями хищника составит:

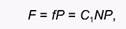(3)

где Р - численность популяции хищника. Теперь мы можем записать уравнение роста популяции жертвы следующим образом:

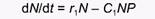(4)

При отсутствии жертвы особи хищника голодают и гибнут. Предполо­жим также, что в этом случае численность популяции хищника будет уменьшаться экспоненциально согласно уравнению:

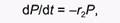(5)

где r₂ - удельная мгновенная смертность в популяции хищника.

Если жертвы присутствуют, то те особи хищника, которые смогут их найти и съесть, будут размножаться. Рождаемость в популяции хищника в данной модели зависит только от двух обстоятельств: скорости потребления жертв хищником и эффективности, с которой поглощенная пища перерабатывается хищником в его потомство. Если мы выразим эту эффективность через коэффициент s, то рождаемость составит:

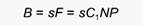
Поскольку С₁ и s - константы, их произведение - это также константа, которую мы обозначим как С₂. Тогда скорость роста популяции хищника будет определяться балансом рождаемости и смертности в соответствии с уравнением:

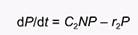(6)

Уравнения 4 и 6 вместе образуют модель Лотки-Вольтерра.

Свойства этой модели мы можем исследовать точно так же, как и в случае конкуренции, т.е. построив фазовую диаграмму, на которой численность жертвы отложена по оси ординат, а хищника - по оси абсцисс, и проведя на ней изоклины-линии, соответствующие постоян­ной численности популяций. С помощью таких изоклин определяют поведение взаимодействующих популяций хищника и жертвы.

Для популяции жертвы: при откуда

Таким образом, поскольку r, и С₁, - константы, изоклиной для жертвы будет линия, на которой численность хищника (Р) является постоянной, т.е. параллельная оси абсцисс и пересекающая ось ординат в точке Р =r₁ /С₁. Выше этой линии численность жертвы будет уменьшаться, а ниже- возрастать.

Для популяции хищника:

при откуда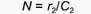

Поскольку r₂ и С₂ - константы, изоклиной для хищника будет линия, на которой численность жертвы (N) является постоянной, т.е. перпендикуляр­ная оси ординат и пересекающая ось абсцисс в точке N = r₂/С₂. Слева от нее численность хищника будет уменьшаться, а справа - возрастать.

Если мы рассмотрим эти две изоклины вместе, то легко заметим, что взаимодействие популяций хищника и жертвы имеет циклический характер, поскольку их численности претерпевают неограниченные сопряженные колебания. Когда велико число жертв, численность хищников растет, что приводит к увеличению пресса хищничества на популяцию жертвы и тем самым к снижению ее численности. Это снижение, в свою очередь, ведет к нехватке пищи у хищников и падению их численности, которое вызывает ослабление пресса хищничества и увеличению численности жертвы, что снова приводит к росту популяции жертвы и т.д.

Для данной модели характерна так называемая "нейтральная стабиль­ность", которая означает, что популяции неограниченно долго совершают один и тот же цикл колебаний до тех пор, пока какое-либо внешнее воздействие не изменит их численность, после чего популяции совершают новый цикл колебаний с иными параметрами. Для того, чтобы циклы стали стабильными, популяции должны после внешнего воздействия стремиться вернуться к первоначальному циклу. Такие циклы, в отличие от нейтрально стабильных колебаний в модели Лотки-Вольтерра, принято называть устойчивыми предельными циклами.

Модель Лотки-Вольтерра, тем не менее, полезна тем, что позволяет продемонстрировать основную тенденцию в отношениях хищник-жертва возникновение циклических сопряженных колебаний численности их популяций.