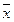Практическая работа № 3 «Представление булевой функции в виде

со­вершенной ДНФ. совершенной КНФ, минимальной ДНФ»

Основные понятия и определения.

Определение. Формула называется тождественно-истинной (тавто-логией), если для любых наборов переменных она принимает значение И.

Определение. Формула называется тождественно тождественно-ложной, если для любых наборов переменных она принимает значение Л.

В алгебре высказываний используют две нормальные формы: дизъюнктивную и конъюнктивную нормальные формы формулы (ДНФ и КНФ).

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.

Конъюнктивной нормальной формой (КНФ) формулы есть формула, равносильная исходной формуле логики высказываний и записанная в виде конъюнкции элементарных дизъюнкций переменных.

Каждая формула, не равная тождественно Л, может быть приведена СДНФ, которая является единственной с точностью до перестановки дизъюнктивных членов.

Каждая формула, не равная тождественно И, может быть приведена к СКНФ, которая является единственной с точностью до перестановки конъюнктивных членов.

Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами

1. Каждое логическое слагаемое формулы содержит все высказывания, входящие в формулу.

2. Все логические слагаемые формулы различны

3. Ни одно логическое слагаемое не содержит высказывание и его отрицание

4. Ни одно логическое слагаемое формулы не содержит одно и то же высказывание дважды.

Алгоритм получения СКНФ по таблице истинности:

1) Отметить те строки , в последнем столбце которых стоят 0:

2) Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =0, то в дизъюнкцию включают саму эту переменную, если =1, то ее отрицание:

3) Все полученные дизъюнкции связать в конъюнкцию.

Образец решения

Построить таблицу истинности для высказывания: 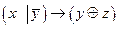, построить СНДФ, СКНФ, найти минимальную ДНФ.

Решение.

Строим таблицу истинности- таблицу, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний.

x	y	z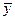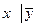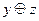

По таблице составляем дизъюнктивную нормальную форму (ДНФ). ДНФ в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции нескольких конъюнктов.

Алгоритм получения СДНФ по таблице истинности:

1) Отметить те строки , в последнем столбце которых стоят 1:

2) Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =1, то в конъюнкцию включают саму эту переменную, если =0, то ее отрицание:

3) Все полученные конъюнкции связать в дизъюнкцию:

Выбираем в таблице строки, в которых булева функция принимает значение 1. В данном случае – это 2-ая, 3-ая, 4-ая, 6-ая и 7-ая строки.

Для каждой строки составляем конъюнкцию: если значение переменной равно 0. то берем ее отрицание, а если 1, то берем саму переменную. Затем составляем дизъюнкцию полученных конъюнкций:

.

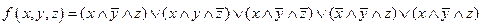Выбираем в таблице строки, в которых булева функция принимает значение 0. В данном случае – это 1-ая, 5-ая, и 8-ая строки:

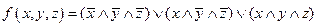
ДНФ называется минимальной, если она содержит наименьшее число букв среди всех ДНФ ей равносильных.

Метод Квайна основывается на применении двух основных соотношений.

Соотношение склеивания :

;

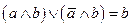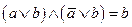
Соотношение поглощения:

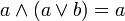
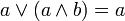
Используя соотношение склеивания получаем:

= ,

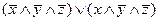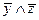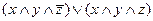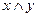= . Отсюда,

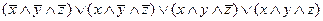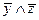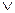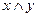=( ) ( )- сокращенная ДНФ

Задания для практической работы: построить таблицу истинности, найти СНДФ, найти минимальную ДНФ для высказывания:

Вариант 1

1.

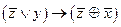
2.

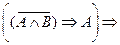
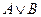
3.

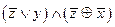
Вариант 2

1.

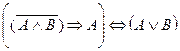
2.

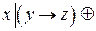
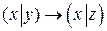
3.

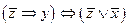
Вариант 3

1.

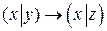
2.

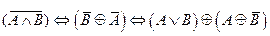
3.

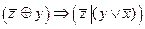
Вариант 4

1.

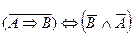
2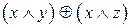

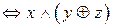
3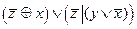

Вариант 5

1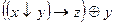

2.

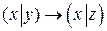
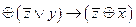
3.

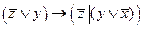
Вариант 6

1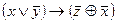

2.

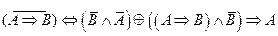
3.

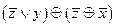
Вариант 7

1.

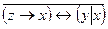
2.

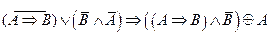
3.

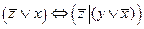
Вариант 8

1.

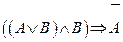
2.

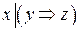
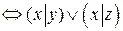
3.

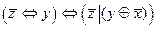
Вариант 9

1 .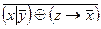

2.

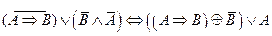
3.

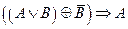
Вариант 10

1.

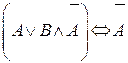
2.

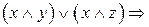
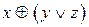
3.

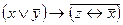
Вариант 11

1 .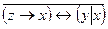

2.

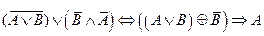
3.

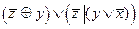
Вариант 12

1.

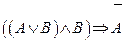
2.

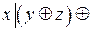
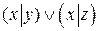
3.

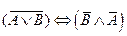
Вариант 13

1.

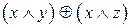
2.

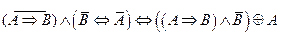
3.

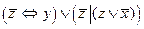
Вариант 14

1.

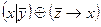
2.

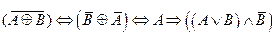
3.

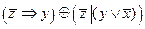
Вариант 15

1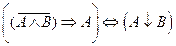

2.

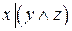
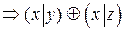
3.

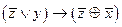
Практическая работа № 4 «Классификация булевых функций;

проверка множества булевых функций на полно­ту»

Основные понятия и определения.

Будем рассматривать логические переменные x₁, x₂, …, x_n, принимающие только два значения: «1» или «0».

Булевой функциейf (x₁, x₂, …, x_n) называется произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0».

Количество булевых функций одного аргумента равно 2² = 4, это функции:

f₁(x) = 0, f₂(x) =1, f₃ (x) = x и f₄(x) = .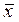

Булевых функций двух аргументов всего 2⁴ = 16, а количество булевых функций n аргументов равно .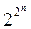

Всякой формуле алгебры логики, составленной из элементарных высказываний x₁, x₂, …, x_n соответствует булева функция f (x₁, x₂, …, x_n), аргументы которой принимают значения истинности соответствующих элементарных высказываний: «1» или «0». Две равносильные формулы алгебры логики определяют одну и ту же булеву функцию, т.к. значения истинности этих формул совпадают для одинаковых значений входящих в них переменных. Для булевых функций можно составлять таблицы значений – всякую булеву функцию n аргументов можно задать таблицей из 2ⁿ строк.

Например, таблица значений некоторых функций 2-х аргументов, соответствующих основным логическим операциям (отрицание одного аргумента, конъюнкция, дизъюнкция, импликация и эквиваленция) выглядит так:

x1	x2		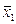x1 Ù x2	x1 Ú x2	x1 ® x2	x1 « x2

Значение булевой функции f (x₁, x₂) при известных значениях аргументов устанавливается по строке таблицы, соответствующей заданным значениям x₁ и x₂. Например, для функции f (x₁, x₂) = x₁ ® x₂ значение f (1, 0) = 0, а значение f (1, 1) = 1.

Каждой релейно-контактной схеме (РКС), составленной из переключателей x₁, x₂, …, x_n, можно поставить в соответствие булеву функцию, называемую ее функцией проводимости:

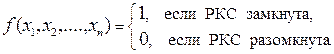
Функция проводимости РКС задается при помощи формулы логики, соответствующей этой РКС. Например, РКС, изображенная на рис. 2,

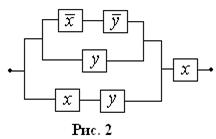
имеет функцию проводимости 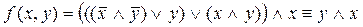, таблица значений которой имеет вид:

х	y	f(x, y)

Любая функция п переменных может быть представлена многочленом (полиномом) Жегалкина и это представление единственно.

Многочлены алгебры логики строятся по аналогии с обычными многочленами. Умножение заменяем конъюнкцией, а сложение альтернативной дизъюнкцией (сложением по модулю два).

Многочленом Жегалкина называется альтернативная дизъюнкция, каждый член которой представляет собой конъюнкцию переменных или переменные, или 1. Любая функция может быть представлена многочленом (полиномом) Жегалкина и это представление единственно. Функция является линейной, если многочлен Жегалкина не содержит конъюнкции переменных.

Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством .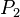

Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:

· Функции, сохраняющие константу 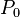и ;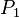

· Самодвойственные функции ;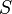

· Монотонные функции ;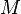

· Линейные функции .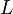

Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с 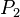, целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом, критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию. Пост доказал, что множество замкнутых классов булевых функций —счётное множество.

Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.

Образец решения:

Записать булеву функцию в виде многочлена Жегалкина. Определить является ли функция линейной.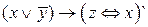

Решение:

Преобразуем равенство, используя формулы алгебры логики.

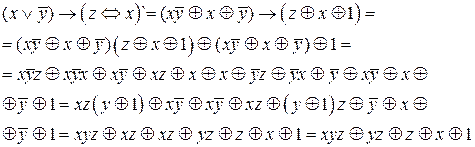
Функция не является линейной, т.к. многочлен Жегалкина содержит конъюнкции переменных.

Ответ: функция не является линейной; многочлен Жегалкина, соответствующий данной функции:

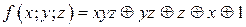
Задания для практической работы:

Вариант 1

Построить функцию, двойственную данной: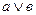

Вариант 2

К какому из классов Поста принадлежит функция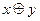

Вариант 3

Построить функцию, двойственную данной: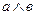

Вариант 4

К какому из классов Поста принадлежит функция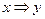

Вариант 5

Построить функцию, двойственную данной: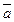

Вариант 6

К какому из классов Поста принадлежит функция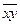

Вариант 7

Построить функцию, двойственную данной: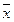

Вариант 8

К какому из классов Поста принадлежит функция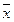

Вариант 9

Построить функцию, двойственную данной: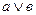

Вариант 10

К какому из классов Поста принадлежит функция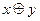

Вариант 11

Построить функцию, двойственную данной: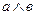

Вариант 12

К какому из классов Поста принадлежит функция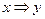

Вариант 13

Построить функцию, двойственную данной: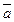

Вариант 14

К какому из классов Поста принадлежит функция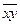

Вариант 15

Построить функцию, двойственную данной: