Теплопередача через плоскую стенку. Коэффициент теплопередачи. Термическое сопротивление
Расчет теплопередачи через плоскую стенку удобно выполнять, используя поверхностную плотность теплового потока
q = Q/F,
где Q – тепловой поток, Вт; F – площадь стенки, м2.
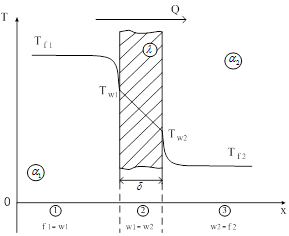
Рис. 5.1. Теплопередача через плоскую стенку
Расчетная схема теплопередачи через плоскую стенку показана на рис. 3.1. Рассмотрим прямую задачу расчета теплопередачи через плоскую стенку при следующих исходных данных:
— толщина плоской стенки равна δ;
— коэффициент теплопроводности стенки λ;
— коэффициент теплоотдачи от горячего флюида к стенке 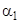 ;
;
— коэффициент теплоотдачи от стенки к холодному флюиду 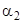 ;
;
— температура горячего флюида 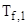 ;
;
— температура холодного флюида 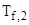 .
.
В результате решения поставленной задачи необходимо найти и плотность теплового потока qи, при заданной площади поверхности теплообмена F, тепловой поток Q, а также температуры на поверхностях стенки 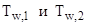 .
.
Краткая форма записи условий прямой задачи теплопередачи имеет вид:
Дано: 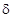 ,
, 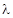 ,
, 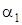 ,
, 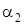 ,
, 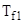 ,
, 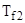 Найти: q,
Найти: q, 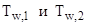
Для решения задачи по расчету теплопередачи через плоскую стенку воспользуемся свойством стационарного режима теплообмена q = const при постоянном λ. Запишем формулы для расчета плотности теплового потока на всех трех участка теплопередачи:
— на 1-ом участке – участке теплоотдачи ( 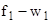 ):
):
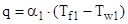
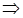
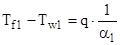 ;
;
— на 2-ом участке – участке теплопроводности ( 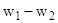 ):
):
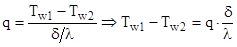 ,
,
— на 3-ем участке – участке теплоотдачи ( 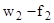 ):
):
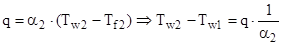 ,
,
Суммируем перепады температур на всех трех участках теплопередачи
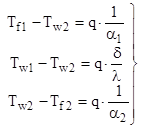 +
+
и, после несложных алгебраических преобразований, получаем выражение для расчета плотности теплового потока через плоскую стенку:
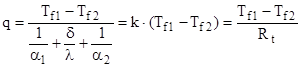 ,
,
где k – коэффициент теплопередачи через плоскую стенку, Вт/(м2·град); 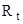 – термическое сопротивление теплопередачи через плоскую стенку, (м2·град)/Вт. Из анализа последней формулы следует, что k и
– термическое сопротивление теплопередачи через плоскую стенку, (м2·град)/Вт. Из анализа последней формулы следует, что k и 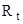 рассчитываются по формулам
рассчитываются по формулам
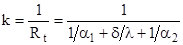 ;
; 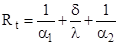 .
.
Термическое или тепловое сопротивление — это свойство материи противостоять изменениям температуры. Когда вещества с высоким термическим сопротивлением используют для изоляции, они хуже проводят тепло. По сравнению с веществами с низким термическим сопротивлением, такие материалы лучше держат температуру. Материалы с высоким термическим сопротивлением используют, когда необходимо поддерживать постоянную температуру внутри камеры или помещения, так как они замедляют утечку тепла в более холодную окружающую среду, или, наоборот, поступление тепла в камеру из более теплой среды.
Термическое сопротивление теплопередачи через плоскую стенку равно сумме термического сопротивления теплоотдачи от горячего флюида к стенке 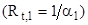 , термического сопротивления теплопроводности плоской стенки
, термического сопротивления теплопроводности плоской стенки 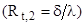 и термического сопротивления теплоотдачи от стенки к холодному теплоносителю
и термического сопротивления теплоотдачи от стенки к холодному теплоносителю 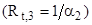 .
.
Прежде чем перейти к определению температурного поля, еще раз подчеркнем, что тепловой поток не изменяется в процессе теплопередачи:
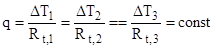 ,
,
где 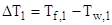 – перепад температур на первом участке теплопередачи – на участке теплоотдачи;
– перепад температур на первом участке теплопередачи – на участке теплоотдачи;
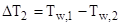 – перепад температур на втором участке теплопередачи – на участке теплопроводности;
– перепад температур на втором участке теплопередачи – на участке теплопроводности;
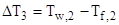 – перепад температур на третьем участке теплопередачи – на участке теплоотдачи.
– перепад температур на третьем участке теплопередачи – на участке теплоотдачи.
Из последнего уравнения по свойству пропорции следует, что
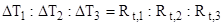 ,
,
т.е. перепад температур, на каком либо участке теплопередачи прямо пропорционален термическому сопротивлению данного участка.
Для расчета неизвестных температур  выберем участок теплообмена таким образом, чтобы на его границах одна температура была известна, а другая искомая.
выберем участок теплообмена таким образом, чтобы на его границах одна температура была известна, а другая искомая.
Например, температуру 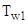 можно найти двумя способами, поскольку по условию задачи заданы две температуры:
можно найти двумя способами, поскольку по условию задачи заданы две температуры:
а) на участке ( 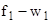 )
)
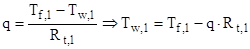 ,
,
б) на участке ( 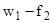 )
)
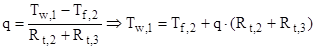 .
.
Естественно, что результаты числового расчета температуры 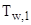 по обеим формулам совпадают.
по обеим формулам совпадают.
Для расчета температуры 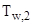 можно воспользоваться уже тремя формулами, поскольку в данном случае мы знаем уже три температуры
можно воспользоваться уже тремя формулами, поскольку в данном случае мы знаем уже три температуры 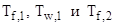 :
:
а) на участке ( 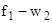 )
)
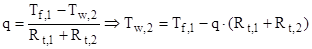 ,
,
б) на участке ( 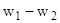 )
)
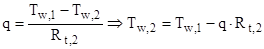 ;
;
в) на участке ( 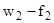 )
)
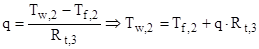 .
.
Для стенки, состоящей из nслоев, формула расчета теплопередачи через плоскую стенку имеет вид:
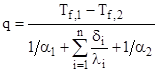 ,
,
где 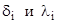 – толщина и коэффициент теплопроводности i-го слоя стенки.
– толщина и коэффициент теплопроводности i-го слоя стенки.
Рекомендуемая последовательность решения:
а) определяют термические сопротивления всех элементарных участков;
б) по двум заданным температурам в системе теплообмена находят плотность теплового потока по формуле (2);
в) по найденному значению q и одной из известных температур рассчитывают остальные неизвестные температуры слоев и жидкостей.
