Как строить эпюру продольных сил?
Установить закон распределения внутренних сил по проведенному сечению методами статики не представляется возможным: составляя уравнения равновесия для сил, приложенных к оставленной части тела, можно лишь найти статический эквивалент внутренних сил (главный вектор и главный момент), возникающих в рассматриваемом сечении.
Указанные шесть внутренних силовых факторов имеют следующие наименования: N, — продольная(или нормальная сила); Q Я„— поперечные силы; М, — крутящиймомент; М„, М„— изгибающие моменты.
4. Расчетная схема является схематизированным представлением реальной конструкции, в котором сознательно не учитывается ряд менее важных с точки зрения проводимого расчета факторов, относящихся к конструктивным особенностям, характеру нагружения и закрепления.
После обоснованного выбора расчетных моделей материала, элемента конструкции, опорных устройств и нагрузок переходят к оценке прочности с помощью моделей разрушения. Модели разрушения представляют собой уравнения связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность. Для большинства конструкций летательных аппаратов рассматривают модели статического разрушения, усталостного разрушения и модели механики разрушения.
5. Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы 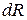 , возникающей на бесконечно малой площадке
, возникающей на бесконечно малой площадке 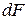 в окрестности данной точки (рис. 1.4, а).
в окрестности данной точки (рис. 1.4, а).
В количественном выражении 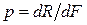 .
.
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).
Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( 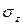 – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (
– сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( 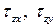 – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
– тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
Между полным ( 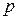 ), нормальным (
), нормальным ( 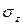 ) и касательными напряжениями (
) и касательными напряжениями ( 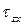 и
и 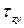 ) существует зависимость:
) существует зависимость:
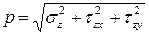 .
.
6. Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х называется сумма произведений элементарных площадок dA на их расстояние y до данной оси, численно равная интегралу:
Sx= 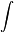 AydA AydA | (1) |
и относительно оси у:
Sy= 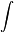 AxdA AxdA | (2) |
Основные свойства статических моментов инерции
· Размерность статического момента — единица длины в третьей степени, обычно [см3] или [м3] .
· Статический момент может быть положительным, отрицательным и равным нулю.
· Ось, относительно которой статический момент равен нулю, называется центральной .
· Точка пересечения центральных осей назвается центром тяжести сечения.
· Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это вытекает со свойств определенного интеграла.
Определение положения центра тяжести
Из формулы (1) и (2) вытекает:
Sx=yc  A
A
Sy=xc  A
A
где A — площадь всей фигуры;
уc — расстояние от центра тяжести фигуры до оси х.
xc — расстояние от центра тяжести фигуры до оси y.
Тогда положение центра тяжести фигуры вычисляется по формулах:
xc=ASy= 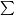 ni=1Ai
ni=1Ai 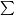 ni=1xi
ni=1xi  Ai
Ai
yc=ASx= 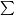 ni=1Ai
ni=1Ai 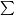 ni=1yi
ni=1yi  Ai
Ai
где Ai  yi
yi  xi – площадь єлементов, на которые разбито сечение и координаты центра тяжести элементов, а n – количество таких элементов.
xi – площадь єлементов, на которые разбито сечение и координаты центра тяжести элементов, а n – количество таких элементов.
Если сечение имеет ось симметрии, то она всегда проходит через центр тяжести, а потому статический момент относительно оси симметрии всегда равен нулю.
7. Осевой момент инерции фигуры - этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:

Центробежный момент инерции фигуры - этоинтеграл произведений элементарных площадей на их расстояния до осей x и y:
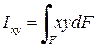
Р 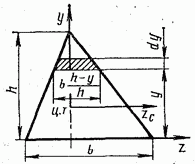 ис. 4.6
ис. 4.6
Рис. 4.7
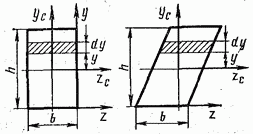
Прямоугольник и параллелограмм (рис. 4.6). Выделим элементарную полоску площадью  и подставим это значение
и подставим это значение  под знак интеграла (4.2):
под знак интеграла (4.2):
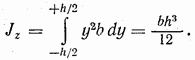
Следовательно, момент инерции прямоугольника и параллелограмма с основанием 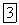 и высотой
и высотой  относительно центральной оси, параллельной основанию,
относительно центральной оси, параллельной основанию,
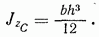
Моменты инерции этих фигур относительно осей, проходящих через основание, находим по формуле (4.12):
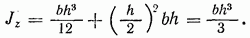
Треугольник с основанием  и высотой
и высотой  (рис. 4.7). Разобьем треугольник на элементарные полоски, параллельные его основанию. Площадь такой полоски
(рис. 4.7). Разобьем треугольник на элементарные полоски, параллельные его основанию. Площадь такой полоски
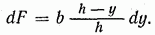
Тогда момент инерции треугольника относительно оси, проходящей через основание,
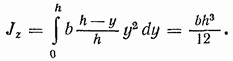
Подсчитывая по формулам переноса момент инерции треугольника относительно центральной оси, параллельной основанию, получаем
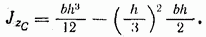
Рис. 4.8
Отсюда относительно центральной оси момент инерции треугольника
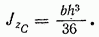
Круг и полукруг диаметра d (рис. 4.8). 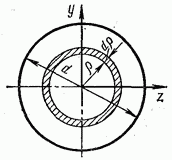
Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиуса  элементарное кольцо площадью
элементарное кольцо площадью  и вычислим
и вычислим  по формуле (4.5):
по формуле (4.5):
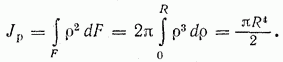
Обычно размеры круглого сечения выражают через диаметр  и подсчитывают
и подсчитывают  по формуле
по формуле
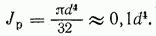
Осевые моменты инерции круга найдем с помощью соотношения  Замечая, что в силу симметрии круга
Замечая, что в силу симметрии круга  получаем для осевых моментов инерции круга выражение
получаем для осевых моментов инерции круга выражение
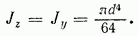
8. Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:
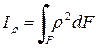
Если через полюс проведена система взаимно перпендикулярных осей x и y, то 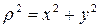 , иформула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:
, иформула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:
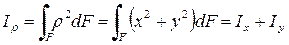
Для круга вначале вычисляют полярный момент инерции, затем — осевые. Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3).
 Площадь каждого кольца можно рассчитать как площадь прямоугольника с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца:
Площадь каждого кольца можно рассчитать как площадь прямоугольника с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца:
dA = 2πρ dρ.
Подставим это выражение для площади в формулу для полярного момента инерции: 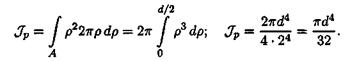
Получим формулу для расчета полярного момента инерции круга: рис. 25.3
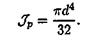
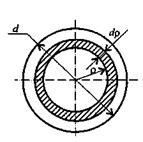
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:
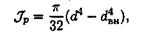
где d — наружный диаметр кольца; dвн — внутренний диаметр кольца.
Если обозначить dвн /d = с, то
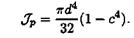
11. Главные оси имеют важное практическое применение. Каким свойством обладают главные оси?
Центробежный момент инерции может быть положительным, отрицательным, а также равным нулю в зависимости от положения координатных осей. Рассмотрим квадрат (рис. 4.2, а).
Центробежный момент инерции квадрата ( 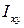 ) относительно осей
) относительно осей 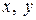 положителен, поскольку координаты
положителен, поскольку координаты 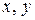 всех элементов площади положительны. При повороте осей вокруг начала координат на угол 900 (рис. 4.2 б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.
всех элементов площади положительны. При повороте осей вокруг начала координат на угол 900 (рис. 4.2 б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.
Можно найти положение двух взаимно перпендикулярных осей, при котором 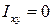 . Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).
. Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).
Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ей перпендикулярна).
Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями.
12. Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:
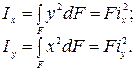
Ввели в рассмотрение еще две геометрические характеристики: радиусы инерции поперечного сечения относительно осей x и y, соответственно. Формула радиуса инерции имеет вид:
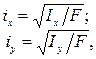
Главным центральным осям инерции соответствуют главные радиусы инерции:
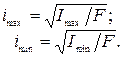
Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:
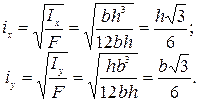
Для круглого сечения формула главных радиусов инерции имеет вид:
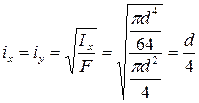
13. Механические свойства материалов
совокупность показателей, характеризующих сопротивлениематериала воз действующей на него нагрузке, его способность деформироваться при этом, а такжеособенности его поведения в процессе разрушения.
Диаграмма деформации. Приложенная к образцу нагрузка вызывает его деформацию
Вид диаграммы деформации не меняется,если по оси ординат откладывать напряжение
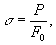
а по оси абсцисс — относительное удлинение
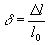
(F0 и l0 — соответственно начальная площадь поперечного сечения и расчётная длина образца).
Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся наединицу площади поперечного сечения образца
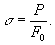
в кгс/мм2. Напряжение
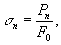
Сопротивление пластической деформации. При нагрузках Р > Рв наряду со всё возрастающей упругой деформацией появляется заметная необратимая, не исчезающая при разгрузке пластическая деформация.
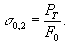
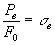
Характеристики пластичности. Пластичность при растяжении конструкционных материаловоценивается удлинением
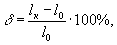
или сужением
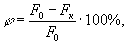
при сжатии — укорочением
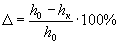
15. Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы 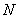 , а прочие силовые факторы равны нулю.
, а прочие силовые факторы равны нулю.
Рассмотрим однородный прямолинейный стержень длиной 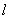 и площадью поперечного сечения А, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).
и площадью поперечного сечения А, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).
Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).
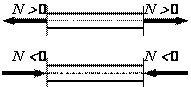
Рис.2.1
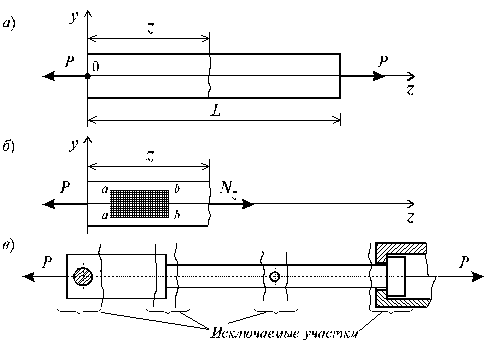
Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение 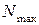 ).
).
КАК СТРОИТЬ ЭПЮРУ ПРОДОЛЬНЫХ СИЛ?
Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).
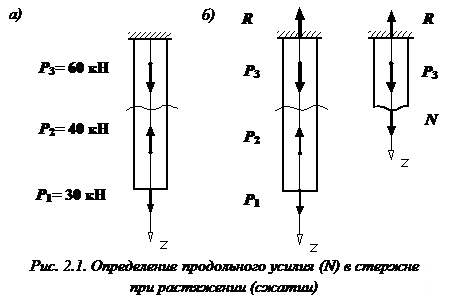
Так как сила 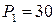 кН растягивает верхнюю часть, а сила
кН растягивает верхнюю часть, а сила 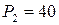 кН ее сжимает, то
кН ее сжимает, то 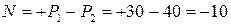 кН.
кН.
Знак «минус» означает, что в этом сечении стержень испытывает сжатие.
Можно найти опорную реакцию R (рис. 2.1, б) и составить уравнение равновесия для всего стержня, чтобы проверить результат:
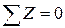
или
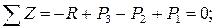
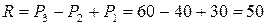 кН.
кН.
Теперь заменим действие отброшенной нижней части неизвестным внутренним усилием N, направив его, например, от сечения, что соответствует растяжению.
Уравновешиваем оставленную нами верхнюю часть стержня:
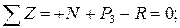
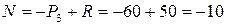 кН.
кН.
Знак «минус» сигнализирует, что мы не угадали направление продольного усилия N. Оно будет не растягивающим, как мы предполагали, а сжимающим.
Таким образом, мы получили тот же самый результат.
16. 2.2. Напряжения в поперечных сечениях бруса
При растяжении (сжатин) бруса в его поперечных сеченияхвозникают тольконормальные напряжения.Равнодействующая соответствующих элементарных сил о, dA — продольная силаN —может быть найдена с помощью метода сечений. Для того чтобы иметь возможность определить нормальные напряжения при известном значении продольной силы, необходимо установить закон нх распределения по поперечному сечению бруса.
Эта задача решается на основе протезы плоских сечений(гипотезы Я. Бернулли), которая гласит:
