Исходные условия эксперимента
Лабораторная работа № 1
Моделирование риска инвестиционного проекта с использованием
Встроенных функций ППП MS Excel 2007
Финансовый риск- уровень финансовой потери, выражающейся либо в возможности не достичь поставленной цели; либо в неопределённости прогнозируемого результата; либо в субъективности оценки прогнозируемого результата.
Статистические критерии риска следующие.
1.Вероятность (Р) события (Е) – отношение числа К случаев благоприятных исходов, к общему числу всех возможных исходов (М):
Р (Е)= К / М
2.Размах вариации (R)– разница между максимальным и минимальным значением фактора:
R=Xmax-Xmin
Этот показатель дает очень грубую оценку риску, т.к. он является абсолютным показателем и зависит только от крайних значений ряда.
3. Дисперсия – сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности.
| к=n |
| Vаr(Е) = S рк (Хк - М(Е))2 , |
| к=1 |
где М(Е) – среднее или ожидаемое значение (математическое ожидание) дискретной случайной величины Е
4. Математическое ожидание определяется как сумма произведений ее значений на их вероятности:
| к=n |
| М(Е)= S Хкрк |
| к=1 |
Это важнейшая характеристика случайной величины, т.к. служит центром распределения ее вероятностей. Смысл ее заключается в том, что она показывает наиболее правдоподобное значение фактора.
4. Среднее квадратическое отклонение s (Е):
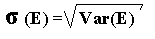
5. Коэффициент вариации (СV):
СV= s(E)/M (E)
Одним из способовоценки финансовых рисков служит имитационное моделирование. В общем случае под имитацией понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира.При анализе рисков инвестиционных проектов обычно используют в качестве базы для экспериментов прогнозные данные об объемах продаж, затратах, ценах и т.п. При проведении финансового анализа часто используются модели, содержащие случайные величины, поведение которых не детерминировано управлением или принимающими решения. Стохастическая имитация известна под названием "метод Монте-Карло".
Имитационное моделирование представляет собой серию численных экспериментов, призванных получить эмпирические оценки степени влияния различных факторов (исходных величин) на некоторые зависящие от них результаты (показатели).
В общем случае проведение имитационного эксперимента можно разбить на следующие этапы:
1. установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства;
2. задать законы распределения вероятностей для ключевых параметров модели;
3. провести компьютерную имитацию значений ключевых параметров модели;
4. рассчитать основные характеристики распределений исходных и выходных показателей;
5. провести анализ полученных результатов и принять решение. Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей сценариев.
Имитационное моделирование рисков может быть достаточно просто реализовано в среде EXCEL.
Исходные условия эксперимента.
Фирма рассматривает инвестиционный проект по производству продукта "А". В процессе предварительного анализа экспертами были выявлены три ключевых параметра проекта и определены возможные границы их изменений (таблица 1.1). Прочие параметры проекта считаются постоянными величинами (таблица 1.2).
Таблица 1.1 - Ключевые параметры проекта по производству продукта "А"
| Показатель | Наихудший | Наилучший | Вероятный |
| Объем выпуска - Q | |||
| Цена за штуку - P | |||
| Переменные затраты - V |
Таблица 1.2 - Неизменяемые параметры проекта по производству продукта"А"
| Показатели | Наиболее вероятное значение |
| Постоянные затраты - F | |
| Амортизация - A | |
| Налог на прибыль - T | 60% |
| Норма дисконта - r | 10% |
| Срок проекта - n | |
| Начальные инвестиции - I0 |
Предположим, что используемым критерием оценки риска является чистая современная стоимость проекта NPV:
n
NPV=S ( NCFt / (1 + r)t - I0)
t=1
где:
NCFt - величина чистого потока платежей в периоде t.
По условиям примера, значения нормы дисконта r и первоначального объема инвестиций I0 известны и считаются постоянными в течение срока реализации проекта (таблица 1.2).
В целях упрощения будем полагать, что величина потока платежей NCF для любого периода t одинакова и может быть определена из следующего соотношения:
NCFt = Qt(Pt – Vt) – F – A)(1 – T) + A
Следующими этапом проведения анализа является выбор законов распределения вероятностей ключевых переменных.
По условиям примера ключевыми варьируемыми параметрами являются: переменные расходы V, объем выпуска Q и цена P. Диапазоны возможных изменений варьируемых показателей приведены в таблице 3.1. При этом будем исходить из предположения, что все ключевые переменные имеют равномерное распределение вероятностей.
Проведение имитационных экспериментов в среде ППП EXCEL можно осуществить двумя способами - с помощью встроенных функций и путем использования инструмента "Генератор случайных чисел" дополнения "Анализ данных" (Analysis ToolPack). Эти инструменты подключаются через пункты меню (Главная кнопка – Параметры - Надстройки – Пакет анализа – Перейти - ОК).
Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9]. В нашем примере необходимо установить режим ручных вычислений (Главная кнопка – Параметры – Формулы – Параметры вычислений – Вручную).
В расчетах будут использоваться функции, описание которых приведено ниже.
