Метод параллельного переноса
Часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и поэтому трудно ввести в чертёж данные. В этих случаях какую-либо часть искомой фигуры переносят или параллельно самой себе, или другим образом, но на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условия задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большее количество данных.
Пример 1. Постройте трапецию по заданным сторонам.
Решение. Анализ. Пусть трапеция АВСD построена, ВС= а, АD= b, AB= c, CD= d (рис. 8). Выполним параллельный перенос, определяемый вектором СВ. Тогда сторона СD перейдёт в BD. Треугольник АВD можно построить по трём сторонам c, d, b-a (b>a).
Затем продолжим отрезок АD на DD = a. Через точку В проведем прямую, параллельную АD и на ней отложим отрезок ВС= а. Соединим точки С и D. Полученная трапеция АВСD – искомая.
План построения очевиден.
Доказательство. В четырехугольнике АВСD BC параллельна AD, значит ABCD – трапеция в которой AB = c, AD =b, так как AD= b – a + a. BD= CD = d.
Исследование. Треугольник ABD можно построить по трём сторонам, если c – d < b – a < c + d. При этом условии однозначно выполнимы и все остальные шаги построения. Если неравенство c – d < b – a < c + d не выполняется, то задача при выбранных данных не имеет решения.
Пример 2. Построить четырёхугольник, зная его углы и противоположные
стороны.
Анализ. Положим, что в четырёхугольнике АВСD стороны BC и AD и углы А, В, С имеют данные значения. Перенесём BC параллельно самой себе в AE, тогда составится треугольник AED, в котором известны две стороны AE и AD и угол EAD, равный разности двух известных углов, данного угла BAD и угла FBC, смежного с данным CBA. Такой треугольник легко построить. Затем легко провести прямые EC и CD, потому что первая образует известный угол с прямой EA (угол CEG равен углу FBC); а вторая образует известный угол CDA со стороною AD. После этого остаётся только провести CB параллельно EA и решение очевидно.
Построение.
1. Строим треугольник АЕD;
2. ЕС;
3. СD;
4. СВ║ЕА.
Исследование.
Эта задача имеет только одно решение: углы и отношение двух противоположных сторон четырёхугольника вполне определяют его вид.
3.1 Метод параллельного переноса
При решении геометрической задачи на построение часто бывает полезной перенести параллельно отдельные части фигуры и тем самым придать ей более удобный для решения вид. [1, стр. 27]
В этом случае применяется параллельный перенос.
Параллельным переносом на вектор 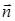 называется преобразование плоскости, которое каждую точку A переводит в такую точку A′, что
называется преобразование плоскости, которое каждую точку A переводит в такую точку A′, что 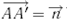 .[4, стр. 5]
.[4, стр. 5]
Перечислим основные свойства параллельного переноса:
§ параллельный перенос является движением I рода;
§ при 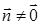 у переноса
у переноса 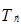 нет инвариантных точек;
нет инвариантных точек;
§ при 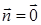 перенос
перенос 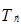 является тождественным преобразование (т.е. все точки плоскости совпадают со своими образами)
является тождественным преобразование (т.е. все точки плоскости совпадают со своими образами) 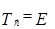 ;
;
§ прямые, параллельные вектору 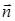 переноса, инвариантны;
переноса, инвариантны;
§ любая прямая, не параллельная вектору 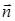 , переходит в параллельную прямую; [8, стр. 8]
, переходит в параллельную прямую; [8, стр. 8]
§ любой луч при 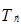 переходит в сонаправленный луч (т.е. геометрический вектор преобразуется в эквивалентный геометрический вектор) – это признак параллельного переноса;
переходит в сонаправленный луч (т.е. геометрический вектор преобразуется в эквивалентный геометрический вектор) – это признак параллельного переноса;
§ параллельный перенос можно представить в виде композиции двух осевых симметрий с параллельными осями;
§ множество всех параллельных переносов плоскости образует группу, являющуюся подгруппой метрической группы. [8, стр. 9]
Для прямолинейных фигур построение их образов в данном переносе осуществляется по нескольким точкам. Для построения образа данной окружности строят образ её центра и, принимая его за центр, проводят окружность тем же радиусом. [3, стр. 93]
Применение параллельного переноса для геометрических построений называют методом параллельного переноса. Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор. Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, [3, стр. 94] когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных. [2, стр. 83]
Если, например, даны два отрезка и угол, между ними заключённый, и если один отрезок будет перенесён параллельно самому себе так, чтобы один из его концов совместился с одним из концов другого отрезка, то получится треугольник, из элементов которого известны две стороны и угол, между ними заключённый. Этот треугольник легко может быть построен, что может оказаться полезным при решении задачи (см. Пример 1). [1, стр. 27]
Особенно часто этим методом параллельного переноса пользуются для построения многоугольников. Иногда также данный метод оказывается полезным при решении задач на «кратчайший путь» (см. Пример 3). [3, стр. 94]
Пример 1. Построить трапецию по заданным её сторонам.
Подробнее: требуется построить трапецию так, чтобы её основания были соответственно равны данным отрезкам a и b (a>b), а боковые стороны были соответственно равны двум данным отрезкам c и d (c 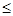 d).
d).
Анализ. Допустим, что ABCD– искомая трапеция, причём AD – её большее основание, BC - меньшее основание, AB и CD – боковые стороны, причём AB=c, CD=d.
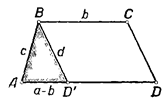
Рис. 1
Представим себе перенос, определяемый вектором 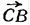 . Тогда (см. Рис.1) сторона CD преобразуется в отрезок BD´. Треугольник АBD´ может быть построен, так как все стороны его известны. Чтобы построить искомую трапецию, останется подвергнуть отрезок BD´ переносу на вектор
. Тогда (см. Рис.1) сторона CD преобразуется в отрезок BD´. Треугольник АBD´ может быть построен, так как все стороны его известны. Чтобы построить искомую трапецию, останется подвергнуть отрезок BD´ переносу на вектор 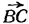 , длина которого известна и который направлен одинаково с вектором
, длина которого известна и который направлен одинаково с вектором 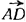 .
.
Построение.
1) Построим треугольник ABD´ по сторонам AB=c, ВD´=d, и AD´=a – b.
2) Через точку В проведём луч, одинаково направленный с лучом AD´.
3) На этом луче построим точку C так, чтобы BC= b.
4) Через C проведём прямую CD параллельно ВD´ до пересечения с продолжением AD´ в точке D. ABCD – искомая трапеция.
Доказательство. AB=c, ВС= b по построению; AD= AD´+ D´D= AD´+ ВС=a – b + b = a. CD=BD´, как отрезки параллельных прямых между параллельными прямыми. [3, стр. 94]
Исследование. Первый шаг выполним при условии:
d – c < a – b < d + c.
При этом условии однозначно выполнимы и все остальные шаги построения. Заметим также, что треугольник ABD´, а следовательно, и трапеция ABCD определяются условиями задачи однозначно до равенства. Поэтому при условии d – c<a – b<d + c задача имеет единственное решение. Если же это условие не выполняется, то задача решения не имеет. [3, стр. 95]
Пример 2. Даны параллельные прямые a и b, пересекающая их прямая c и отрезок длины m. Построить равносторонний треугольник со стороной данной длины m, так, чтобы его вершины лежали соответственно на данных прямых.
Решение
Анализ. Пусть искомый треугольник ABC построен: A 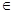 a, B
a, B 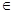 b, C
b, C 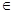 c и
c и 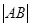 =
= 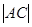 =
= 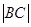 = m( см. Рис. 2). Выполним параллельный перенос
= m( см. Рис. 2). Выполним параллельный перенос 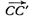 треугольника ABC, причём
треугольника ABC, причём 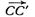 || a. Получим треугольник A´B´C´ со сторонами данной длины m, причём A´
|| a. Получим треугольник A´B´C´ со сторонами данной длины m, причём A´ 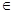 a, B´
a, B´ 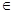 b.
b.
Так как треугольник A´B´C´, две вершины которого лежат на прямых a и b, построить не трудно, то на этом анализ можно закончить. Таким образом, задачу можно свести к построению равностороннего треугольника A´B´C´ со стороной длины m, причём A´ 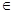 a, B´
a, B´ 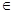 b, а затем к последующему параллельному переносу
b, а затем к последующему параллельному переносу 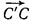 треугольника A´B´C´, причём С вектора
треугольника A´B´C´, причём С вектора 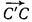 определяется как точка пересечения прямой
определяется как точка пересечения прямой 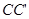 || a с данной прямой с. [4, стр. 37]
|| a с данной прямой с. [4, стр. 37]
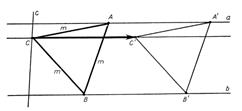
Рис. 2
Построение (см. Рис. 3.). Выбираем произвольную точку A´  a. Описываем окружность
a. Описываем окружность 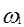 = (A´, m). Находи точку B´ =
= (A´, m). Находи точку B´ = 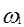
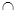 b. Описываем окружность
b. Описываем окружность 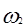 = (В´, m). Находим точку С´ =
= (В´, m). Находим точку С´ = 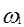
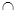
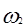 . Через точку
. Через точку 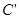 проводим прямую k || a и находим точку С = k
проводим прямую k || a и находим точку С = k  a. Откладываем
a. Откладываем 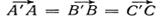 и получаем треугольник ABC.
и получаем треугольник ABC.
Рис. 3
Доказательство. По построению треугольника A´B´C´ удовлетворяет всем поставленным условиям, кроме условия C´ 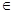 с. После параллельного переноса
с. После параллельного переноса 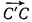 удовлетворяется и это условие. Таким образом,
удовлетворяется и это условие. Таким образом, 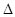 ABC – искомый.
ABC – искомый.
Исследование. При выбранном способе построения число решений задачи зависит, прежде всего, от числа точек B´ = 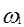
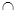 b.
b.
Если радиус m окружности 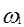 больше расстояния h между прямымиa и b, то таких точек две.
больше расстояния h между прямымиa и b, то таких точек две.
Если m = h окружности 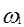 касается прямой b, и тогда точка пересечения одна.
касается прямой b, и тогда точка пересечения одна.
Если же m<h, то окружность 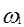 и прямая b не пересекается. Окружности
и прямая b не пересекается. Окружности 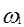 и
и 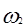 всегда имеют общие точки, так как по построению В´
всегда имеют общие точки, так как по построению В´ 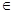
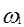 , A´
, A´ 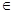
 , . Значит, при любом выборе точки A´ образуется две точки пересечения окружностей
, . Значит, при любом выборе точки A´ образуется две точки пересечения окружностей  и
и  .
.
Итак, возможны три следующих случая:
1) если m>h, то задача имеет четыре решения (см. Рис. 4 а),
2) если m = h, то задача имеет два решения (см. Рис. 4 б),
3) если m<h, то задача не имеет решений. [4, стр. 38]
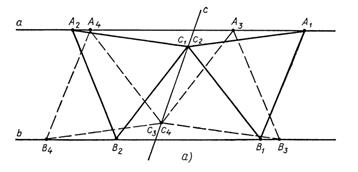
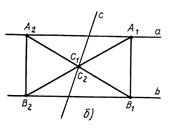
Рис. 4.
Пример 3. Между пунктами А и В течёт канал. Где следует выбрать место для моста, чтобы путь от А до В был кратчайшим.
Представим себе берега канала в виде двух параллельных прямых a и b (см. Рис. 5, а), а мост – в виде отрезка MN, перпендикулярного к этим прямым.
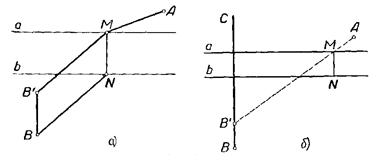
Рис. 5
Задача заключается в том, чтобы выбрать такое положение точки M на прямой a (или точки N на прямой b), чтобы ломанная AMNB имела наименьшую длину.
Так как длина отрезка MN постоянная, то условие задачи равносильно требованию, чтобы сумма отрезков AM и NB была наименьшей.
Чтобы связать отрезки AM и NB, перенесём отрезок BN на вектор 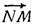 . Тогда точка N перейдёт в точку M, а точка В – в некоторую точку B´, которая легко может быть построена. Так как BN= B´M, то нужно найти такое положение точки M, при котором ломанная B´АM, концы которой известны, имела бы наименьшую длину. Ясно, что это будет в случае, когда точки B´, А и M расположатся на одной прямой. [3, стр. 98]
. Тогда точка N перейдёт в точку M, а точка В – в некоторую точку B´, которая легко может быть построена. Так как BN= B´M, то нужно найти такое положение точки M, при котором ломанная B´АM, концы которой известны, имела бы наименьшую длину. Ясно, что это будет в случае, когда точки B´, А и M расположатся на одной прямой. [3, стр. 98]
Построение показано на рисунке 5, б. Проводим прямую BС перпендикулярно прямой a и откладываем на ней отрезок BB´, равны шире канала. Строим прямую АB´. Прямая АB´ пересекает прямую a в искомой точке M.
Задача всегда имеет решение, притом единственное. [3, стр. 99]
