Пример составления математической модели состояния объекта

3.2.1. Описание объекта моделирования. Идеализация объекта. Построение ММ. Исследование пространства состояний.

Рассмотрим в качестве объекта исследования машинно-тракторный агрегат (МТА) при составлении математической модели формирования средней крюковой нагрузки трактора.

Задача, которая должна быть решена с помощью составления математической модели, требует найти способ снижения динамической составляющей средней крюковой нагрузкитрактора в составе МTA.

Описание объекта. Объект состоит из трактора (любого - колесного или гусеничного) и рабочей сельскохозяйственной машины, взаимодействующей с объектом обработки, например, с почвой. При наличии неоднородностей в почве и попадании на них рабочих органов возникнут динамические составляющие крюкового нагружения, которые приведут к росту среднего значения крюковой нагрузки. Динамичность нагружения можно оценить величиной импульсов увеличения нагрузки. При более или менее равномерном расположении неоднородностей горизонтальное сопротивление передвижению МТА со стороны рабочих органов машины можно представить в виде закона нагружения, показанного на рис.3.1.

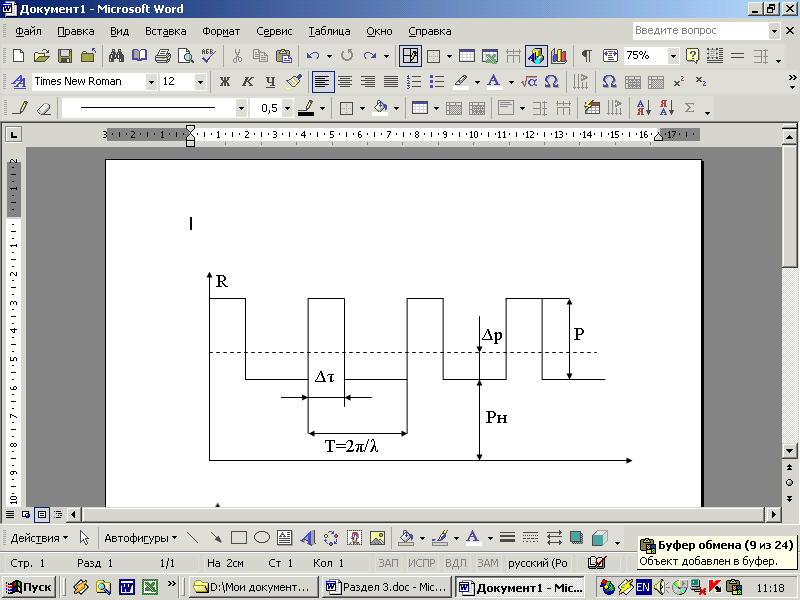
Рис.3.1. Закон нагружения МТА на поле с равномерно

расположенными неоднородностями

Величина Р_н- нижний уровень сопротивления обрабатываемого материала, определяемый состоянием его основной массы; Р∆τ - импульс воздействия неоднородностей; Т=2π/λ- период между неоднородностями (λ - угловая частота появления импульсов).

В результате взаимодействия обрабатываемого материала с динамической системой МТАна крюке формируется нагрузка трактора в виде плавно изменяющейся силы (рис.3.2).

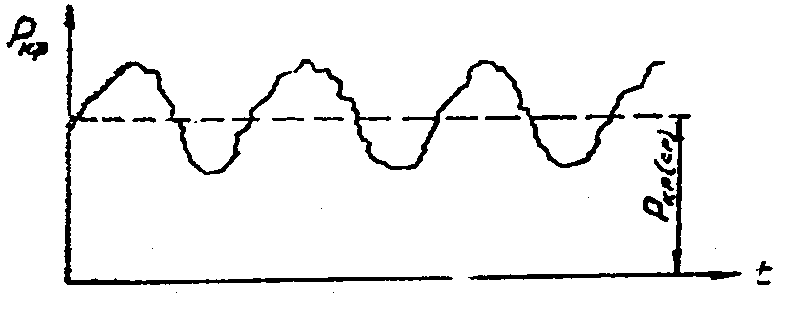
Рис. 3.2. Крюковая нагрузка трактора

В составе среднего крюкового усилия имеется и динамическая составляющая ∆р,величина которой определяет снижение производительности МТА, увеличение затрат топлива на выполнение работы. Для нахождения путей снижения величины ∆р надо установить зависимость ∆р от характера нагружения, основных параметров и констант рассматриваемой системы. Величина Р∆τ будет определяться:

1. величиной массы МТА;

2. скоростью движения МТА;

3. жесткостью конструкции сочленения сельскохозяйственной машины и трактора;

4. упругими свойствами валопровода, соединяющего коленвал двигателя с ведущим элементом движителя;

5. характеристикой двигателя (ее свойствами, обеспечивающими возможность преодоления временного сопротивления);

6. жесткостью самой ходовой системы.

Перечисленные параметры свидетельствуют о сложности задачи оценки динамического прироста среднего крюкового усилия. Решение ее осложняется и информативной неопределенностью, связанной с неизвестностью закона расположения неоднородностей в почве и характеристик этих неоднородностей. Короче говоря, нам неизвестен сам импульс и закон его формирования. Изображение его в виде постоянной силы Р в промежутке времени ∆τ условно. Реальное его протекание трудно установить, даже если будет известна разница физико-химических свойств основного материала и неоднородностей.

Учитывая сказанное по поводу информативной неопределенности импульса силы сопротивления, а также самого нижнего уровня его Р_н , мы вряд ли сможем точно описать совмещение параметров машины по нагружению с характеристикой двигателя и получить решение о величине Р_кр(ср). Вернее, наша задача в этом случае разбивается на ряд задач с конкретными уровнями Р_ни значений Р.

Как и во всякой задаче, необходимо обойти эту неопределенность и решить задачу не количественными мерами, а качественными: обосновать критерий минимизации динамической составляющей, не рассматривая с количественной стороны величину снижения ∆р.

В этом случае мы сможем сделать достаточно большое количество допущений, существенно упрощающих объект, приняв его абсолютно жестким с точки зрения параметров системы (пункты 3...6),определяющих величину импульса. Тогда объект исследования превратится в одномассовую систему, движущуюся со скоростью v и обладающую массой m_мта=m_тр+m, где m_тр - приведенная масса трактора; m– масса машины. Принципиальная схема нагружения агрегата представлена на рис3.3.

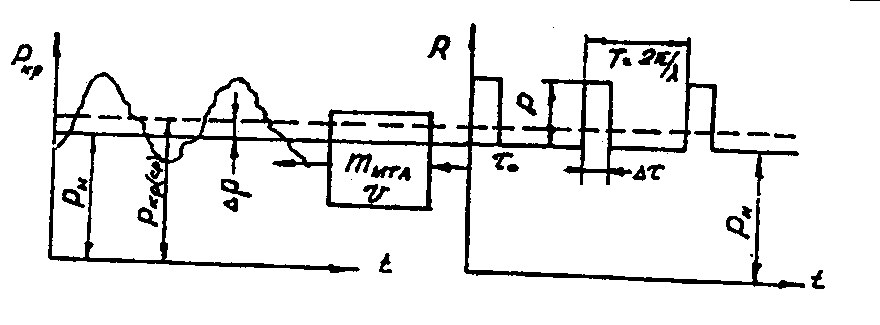
Рис.3.3. Принципиальная схема преобразования нагружения машины машинно-тракторным агрегатом

В качестве входной переменной в этой задаче рассматривается сопротивление обрабатываемого материала при принятых ранее допущениях, а выходной переменной не само среднее крюковое усилие, а его динамическая составляющая ∆р.

Пространство состояний объекта непрерывно при принятых допущениях и детерминировано. Состояние объекта может быть описано в этом случае дифференциальным уравнением движения при переменном внешнем воздействии (R-var). Однако, как уже было сказано, в них отразится неопределенность информации о силе сопротивления материала обработке. Значит, требуется новое допущение, которое позволит математически описать состояние объекта.

Рассмотрим состояние объекта на одном периоде, учитывая допущение об одинаковости последующих импульсов и абсолютной жесткости системы, исключающей появление резонансных явлений. Процесс взаимодействия неоднородностей обрабатываемого материала и рабочих органов как элементов абсолютно жесткой системы МТА можно рассматривать как явление удара.

Составление математической модели. Результат этого взаимодействия можно оценить по снижению кинетической энергии движущегося тела (МТА) при попадании на препятствие:

,

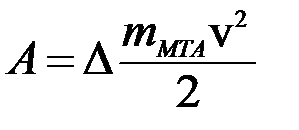где А - энергия, вызывающая возрастание импульса силы при ударе; ∆- знак дифференциала. Тогда можно записать: А=m_мтаv∆v, где ∆v – снижение скорости МТА при встрече с препятствием.

Откуда 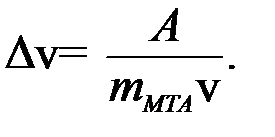(3.1)

Последнее выражение и будет математической модельюсостояния объекта, характеризующей снижение скорости в промежутке времени Т при наличии импульса силы А.

Возвратившись к принципиальной схеме, обратим внимание на то, что в качестве выходной переменной в ней использована динамическая составляющая среднего крюкового усилия ∆р. Если усреднить импульс силы в промежутке времени между соударениями, то энергию удара можно будет подсчитать через искомую величину ∆р:

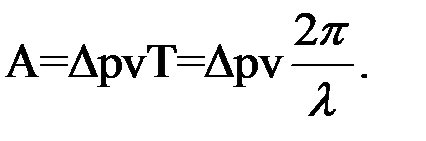(3.1)

Подставив это выражение в зависимость (3.1), получим

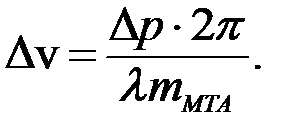(3.2)

В этой форме ММ состояния констатирует связь динамической составляющей крюкового усилия с уменьшением скорости МТА, которое может быть зафиксировано.

3.2.2. Закономерности, действующие в области применения модели.

Математическая формулировка этих закономерностей

Выражение (3.2) характеризует изменение состояния объекта (МТА) в худшую сторону с появлением импульса Р∆τ при ранее принятой закономерности. Наша цель состоит в определении условий взаимодействия орудия с обрабатываемым материалом, при которых возможно снижение динамической составляющей ∆р. Введение упругого элемента в сочленение трактора и машины позволяет при воздействии силой ∆р со стороны препятствия получить ускорение, замедляющее наезд рабочего органа на препятствие, а значит, аккумулировать энергию удара для последующего ее использования. При принятых допущениях замед­ление наезда на препятствие можно оценить выражением 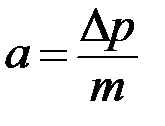, где а - ускорение (замедление) сельскохозяйственной машины при наезде на препятствие в результате сжатия упругого элемента; m -масса сельскохозяйственной машины.

Деформация упругого элемента х при условии равноускоренного замедления машины составит

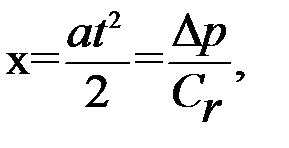
где С_r– горизонтальная жесткость упругого элемента в сочленении трактора и сельскохозяйственного орудия, Н/м; t – время действия импульса, ∆р – динамическая составляющая крюкового усилия.

Отсюда 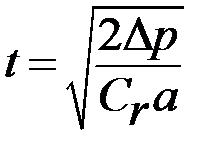, а поэтому максимальное снижение скорости соударения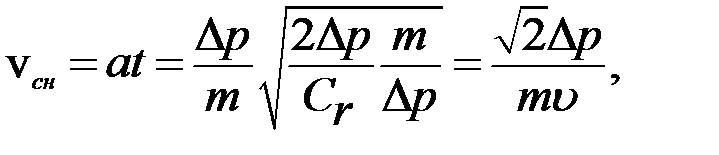

где 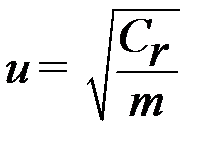- частота собственных колебаний сельскохозяйственной машины.

Устранения (максимально возможного снижения) динамической составляющей при взаимодействии сельскохозяйственной машины с препятствием следует ожидать при условии

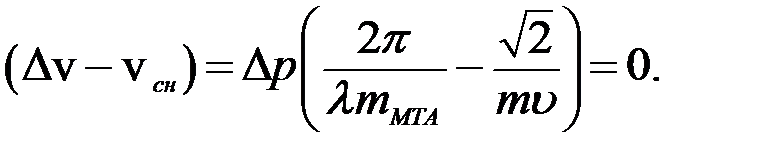
Из последнего выражения следует зависимость: 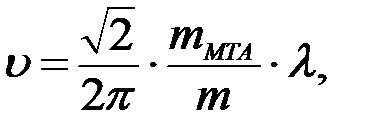которая может быть представлена в следующем виде:

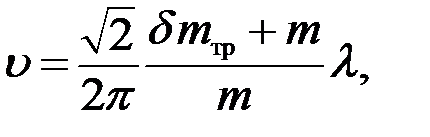(3.3)

где δ - коэффициент учета вращающихся масс трактора.

Подсчитанное значение υ дает возможность определить жесткость упругого элемента, снижающего динамическую составляющую от соударений с препятствиями, которые соответствуют колебаниям с частотой λ.

Мы рассматривали эту задачу, позволяющую нам получить решение в аналитической форме, не прибегая к ЭВМ, для демонстрации возможности идеализации объекта (упрощения). Этот шаг больше всего подвергается критике со стороны оппонентов: легче доказать непригодность исходной принципиальной модели (особенно для сложной системы), чем разбираться в математических тонкостях алгоритма ее расчета на ЭВМ.

Экспериментальный материал доказал адекватность математической модели реальному процессу (при заданной цели) не только качественно, но и количественно: выигрыш по среднему крюковому усилию оказался выше на работах с заведомо бóльшим исходным импульсом динамичности процесса.

Все это подробно рассмотрено для того, чтобы показать особую важность первого шага на пути создания ММ: построения физической модели (принципиальной схемы) и обоснования принятых допущений