Тема(4) Показники надійності систем керування електроприводами
Показатели и количественные характеристики надежности
Средней наработкой до отказа 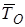 называется математическое ожидание наработки изделия до первого отказа.
называется математическое ожидание наработки изделия до первого отказа.
Как математическое ожидание 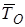 вычисляется через частоту отказов (плотность распределения времени безотказной работы):
вычисляется через частоту отказов (плотность распределения времени безотказной работы):
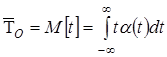 . (1.8)
. (1.8)
Так как t положительно и 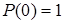 , а
, а 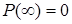 , то
, то

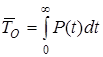 . (1.9)
. (1.9)
По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле
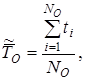 (1.10)
(1.10)
где 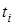 – время безотказной работы i- го изделия,
– время безотказной работы i- го изделия, 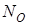 - число испытуемых изделий.
- число испытуемых изделий.
Имея данные о количестве вышедших из строя изделий 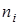 в каждом i-ом интервале времени, среднюю наработку до первого отказа лучше определить из выражения
в каждом i-ом интервале времени, среднюю наработку до первого отказа лучше определить из выражения
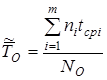 . (1.11)
. (1.11)
В выражении (1.11) 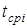 и m находятся по следующим формулам
и m находятся по следующим формулам
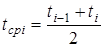 ,
, 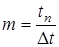 ,
,
где 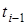 - время начала i-ого интервала;
- время начала i-ого интервала; 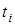 - время конца i-ого интервала;
- время конца i-ого интервала; 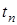 - время, в течение которого вышли из строя все изделия;
- время, в течение которого вышли из строя все изделия; 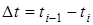 - интервал времени.
- интервал времени.
Таблица 1.1. Основные соотношения количественных характеристик надежности
| Закон распределения | Частота отказов 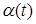 | Вероятность безотказной работы 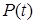 | Интенсивность отказа 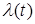 |
| Экспоненциальный | 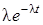 | 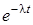 | 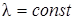 |
Из выражений для оценки количественных характеристик надежности видно, что все характеристики являются функциями времени. На рис. 1.2 приведены зависимости количественных характеристик надежности изделий от времени.
| а |  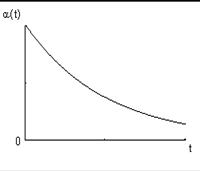 |  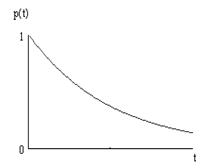 |  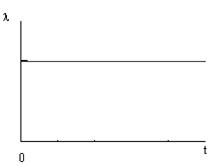 |
Рассмотрим показатели надёжности восстанавливаемых систем.
Средняя наработка на отказ есть отношение наработки восстанавливаемого изделия к математическому ожиданию числа его отказов в течение этой наработки.
Эта характеристика определяется по статистическим данным об отказах по формуле
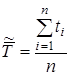 , (1.13)
, (1.13)
где 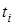 - время исправной работы изделия между (i – 1)-м и i-м отказами; n – число отказов за некоторое время t.
- время исправной работы изделия между (i – 1)-м и i-м отказами; n – число отказов за некоторое время t.
Среднее время восстановления есть математическое ожидание времени восстановления работоспособного состояния объекта.
По статистическим данным среднее время восстановления вычисляется по формуле:
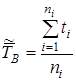 (1.19)
(1.19)
Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок.
Согласно определению
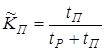 (1.20)
(1.20)
или переходя к средним величинам,
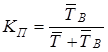 (1.21)
(1.21)
Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью
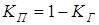 . (1.22)
. (1.22)
При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле
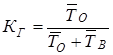 (1.23)
(1.23)
ДЗ СРС4 Подготовиься к ПР1
