Дополнительные указания. Выбор оптимального варианта переработки заданного вида груза осуществляется с

Выбор оптимального варианта переработки заданного вида груза осуществляется с учётом главных логистических принципов:

1. Минимальные затраты.

2. Точно в срок.

3. Безусловная сохранность груза.

Требования к оформлению отчёта

Отчёт студенты оформляют в следующей последовательности:

1. Цель работы.

2. Описание метода тактического планирования с изображением цепочки.

3. Описание технологии переработки груза с подробным описанием прибывающего вида транспорта и типа ПС, поступление в склад (с указанием его типа и чем его доставляют) или выгрузка по прямому варианту, сочетающую и погрузку в судно. Технология должна иметь вид текста, а не набор наименований с их величинами.

При непрямом варианте предоставляют технологию переработки заданного груза через склад.

12.6 Контрольные вопросы

1.Для чего строится цепочка тактического планирования?

2.Какие логистические критерии вы знаете?

Лабораторная работа № 13.
Транспортная логистика. Прикрепление поставщиков к потребителям

Цель:решение транспортной задачи с использованием стандартной компьютерной программы EXСEL.

Теоретические положения

Классическая транспортная задача заключается в оптимальном закреплении поставщиков груза за потребителями. Необходимо так закрепить потребителей груза за грузоотправителями, чтобы общая транспортная работа была минимальной.

Ввиду особенностей математической формы и постановки транспортной задачи линейного программирования для решения её разработаны специальные методы, позволяющие из бесчисленного множества возможных решений найти оптимальное. Одним из них является распределительный, имеющий несколько разновидностей, которые отличаются в основном способом выявления оптимального решения.

Самым простым способом решения транспортной задачи является способ северо-западного угла. Пример решения подробно рассмотрен в п.13.3. Другие способы весьма трудоёмки для ручного расчёта и в данной лабораторной работе не рассматриваются. Математическая модель этой задачи такова:

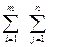C_IJ Х_IJ ® min;

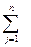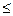Х_IJ a_i , i = 1,2, …, m; (13.1)

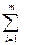Х_IJ 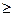b_j , j = 1,2, …, n;

Х_IJ 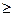0, i = 1,2, …, m; j = 1,2, …, n,

где i – количество поставщиков;

j – количество потребителей;

a_i – ограничение по предложению;

b_j – ограничение по спросу;

C_IJ – стоимость перевозки единицы продукции от i–го поставщика к j–му потребителю;

Х_IJ – объём корреспонденции между i-й и j-й точками.

Критерием оптимальности в транспортной задаче может быть затраты времени, стоимость, расстояние перевозки или др.

Задание на работу

Требуется установить такие объёмы перевозок Х_IJ от каждого поставщика к каждому потребителю, чтобы суммарные затраты на перевозки были минимальными и потребности всех потребителей были удовлетворены. Задачу решить с помощью ПЭВМ двумя способами:

1.Методом северо-западного угла.

2.В стандартной программе EXСEL.

Исходные данные по варианту приведены в табл. 13.1.

Таблица 13.1.

№ вар	Поставщики	Потребители
1-ый	2-ой	3-ий	4-ый	5-ый	1-ый	2-ой	3-ий	4-ый	5-ый
										Величину поставки для 5-го потребителя студенты рассчитывают самостоя- тельно.
										Величину поставки для 5-го потребителя студенты рассчитывают самостоя- тельно.

Стоимость перевозки от i–го поставщика к j–му потребителю приведена в табл. 13.2.

Таблица 13.2.

КJ ПI	К1	К2	К3	К4	К5
П1
П2
П3
П4
П5