Лабораторная работа №5. Интерполирование функции, заданной таблично, по формулам Лагранжа и Ньютона
Интерполирование функции, заданной таблично, по формулам Лагранжа и Ньютона. Оценка погрешностей интерполирования
(4часа)
Цель:сформировать у студентов умение интерполировать функции, заданные таблично, используя современные программные средства
Задания: Найти коэффициенты интерполяционных многочленов Лагранжа и Ньютона. Построить графики интерполяционных многочленов.
В таблице 6 приведены варианты заданий.
Таблица 6 - Варианты заданий
| № Вар. | Задание | ||||
| xi | 0,4 | 0,7 | 1,0 | 1,3 | |
| yi | 1,8235 | 2,778 | 4,245 | 6,364 |
Продолжение таблицы 6.
| xi | 0,5 | 0,8 | 1,1 | 1,4 | |
| yi | 1,925 | 3,123 | 5,03 | 7,829 | |
| xi | 0,3 | 0,5 | 0,7 | 0,9 | |
| yi | 1,622 | 2,16 | 2,895 | 3,913 | |
| xi | 0,5 | 0,9 | 1,3 | 1,7 | |
| yi | 1,622 | 2,913 | 5,126 | 8,557 | |
| xi | 0,3 | 0,6 | 0,9 | 1,2 | |
| yi | 1,421 | 2,116 | 3,231 | 4,896 | |
| xi | 0,3 | 0,7 | 1,1 | 1,5 | |
| yi | 1,671 | 2,866 | 8,431 | ||
| xi | 0,4 | 0,6 | 0,8 | ||
| yi | 1,579 | 2,037 | 2,694 | 3,594 | |
| xi | 0,5 | 0,7 | 0,9 | 1,1 | |
| yi | 1,887 | 2,643 | 3,693 | 5,099 | |
| xi | 0,4 | 0,8 | 1,2 | 1,6 | |
| yi | 1,497 | 2,962 | 5,687 | 10,092 | |
| xi | 0,5 | 0,8 | 1,1 | 1,4 | |
| yi | 1,962 | 3,036 | 4,739 | 7,226 |
Окончание таблицы 6
| xi | 0,5 | 0,9 | 1,3 | 1,7 | |
| yi | 2,076 | 3,607 | 6,26 | 10,409 | |
| xi | 0,3 | 0,5 | 0,7 | 0,9 | |
| yi | 1,185 | 1,557 | 2,096 | 2,831 | |
| xi | 0,5 | 0,9 | 1,3 | 1,7 | |
| yi | 1,622 | 2,913 | 5,126 | 8,557 | |
| xi | 0,3 | 0,6 | 0,9 | 1,2 | |
| yi | 1,421 | 2,116 | 3,231 | 4,896 | |
| xi | 0,3 | 0,7 | 1,1 | 1,5 | |
| yi | 1,671 | 2,866 | 8,431 |
Контрольные вопросы
1. Сформулируйте постановку задачи интерполяции функции.
2. Запишите формулы интерполяционного многочлена Лагранжа.
3. Запишите формулу интерполяционного многочлена Ньютона.
4. Как оценить погрешность интерполяционной формулы?
5. Дайте понятие сплайна и изложите суть сплайн-интерполяции.
Лабораторная работа №6
Метод наименьших квадратов. Построение линии регрессии. Обработка экспериментальных данных
(4часа)
Цель: Сформировать у студентов умение подбирать функции, описывающие эмпирические зависимости.
Задания: 1.Даны 25 значений функции у и некоторое начальное значение независимой переменной х. Известно, что независимая переменная х изменяется с постоянным шагом h=0,2. Требуется подобрать аналитическую зависимость, описывающую опытные данные наилучшим образом. Варианты индивидуальных заданий приведены в таблицах 7.1 и 7.2.
2. Решить задачу прикладного характера, используя метод наименьших квадратов.
Таблица 7.1 - Варианты индивидуальных заданий (№1 -8)
| № варианта | ||||||||
| х | 1,1 | 0,4 | 1,4 | 0,7 | 1,3 | 2,5 | 1,5 | 2,1 |
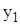 | -4,885 | -0,751 | -4,702 | -8,431 | -7,342 | -6,942 | -8,321 | -2,215 |
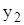 | -3,284 | -0,599 | -3,531 | -7,242 | -5,002 | -6,202 | -6,451 | -2,103 |
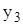 | -2,037 | -0,371 | -2,944 | -6,542 | -4,203 | -5,403 | -4,335 | -1,435 |
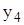 | -1,723 | -0,204 | -1,832 | -5,321 | -3,109 | -2,009 | -2,944 | -0,348 |
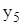 | -0,952 | -0,24 | -0,771 | -4,284 | -1,002 | -1,507 | -1,431 | 0,102 |
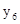 | 0,093 | 0,073 | -0,351 | -3,102 | -0,932 | -0,308 | -0,592 | 0,308 |
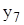 | 0,287 | 0,134 | -0,009 | -2,952 | 0,051 | -0,741 | 0,748 | 1,205 |
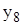 | 0,694 | 0,26 | 0,241 | -1,008 | 0,632 | -1,581 | 1,244 | 2,505 |
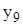 | 1,239 | 0,267 | 0,549 | -0,941 | 0,944 | -0,005 | 3,144 | 3,009 |
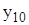 | 1,592 | 0,447 | 0,708 | 0,009 | 1,532 | 1,604 | 4,232 | 4,204 |
Окончание таблицы 7.1
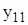 | 1,708 | 0,809 | 1,453 | 0,974 | 2,271 | 3,242 | 5,808 | 5,051 |
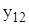 | 1,77 | 0,835 | 2,561 | 1,989 | 3,025 | 5,252 | 6,209 | 5,321 |
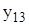 | 1,784 | 0,905 | 3,271 | 2,323 | 3,942 | 7,485 | 6,432 | 4,939 |
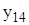 | 1,748 | 0,906 | 3,782 | 3,054 | 4,621 | 7,483 | 5,904 | 3,922 |
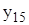 | 1,652 | 0,768 | 2,543 | 3,204 | 4,232 | 6,532 | 4,401 | 2,343 |
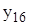 | 1,456 | 0,809 | 1,441 | 2,902 | 4,029 | 5,342 | 3,105 | 2,004 |
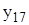 | 0,876 | 0,753 | 0,008 | 2,382 | 3,602 | 2,248 | 1,422 | 1,934 |
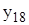 | 0,568 | 0,714 | -0,902 | 1,525 | 1,937 | 3,002 | 0,303 | 0,672 |
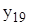 | -0,039 | 0,632 | -0,994 | 0,908 | 0,567 | 1,947 | -0,561 | -0,943 |
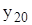 | -0,374 | 0,532 | -2,008 | 0,001 | -0,003 | -0,211 | -0,944 | -0,947 |
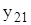 | -0,726 | -0,974 | -3,631 | -0,941 | -0,302 | 0,348 | -1,438 | -1,063 |
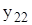 | -1,48 | -1,374 | -4,748 | -1,342 | -1,942 | -0,698 | -3,943 | -2,005 |
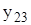 | -2,301 | -1,994 | -5,548 | -2,546 | -2,432 | -2,451 | -4,563 | -2,544 |
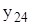 | -3,195 | -2,396 | -5,901 | -3,744 | -4,323 | -4,691 | -5,442 | -2,963 |
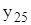 | -3,673 | -2,934 | -6,402 | -4,892 | -4,598 | -6,308 | -6,728 | -3,002 |
Таблица 7.2 - Варианты индивидуальных заданий (№9 -15)
| № варианта | |||||||
| х | 3,1 | 2,7 | 0,5 | 1,8 | 2,4 | 3,7 | 2,9 |
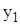 | -1,602 | -4,967 | -10,32 | -2,123 | -1,602 | -3,851 | -7,561 |
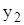 | -1,061 | -3,543 | -8,451 | -1,465 | -1,064 | -2,801 | -5,543 |
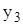 | -0,973 | -2,821 | -6,665 | -1,117 | -0,878 | -2,144 | -3,339 |
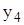 | -0,521 | -1,944 | -5,332 | -0,853 | -0,623 | -1,439 | -2,701 |
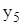 | -0,102 | -1,202 | -2,721 | -0,094 | -0,203 | -0,594 | -1,909 |
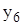 | -0,009 | -0,938 | -1,319 | 0,324 | 0,093 | -0,007 | -1,011 |
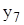 | 0,371 | -0,752 | -0,944 | 0,792 | 0,374 | 0,651 | -0,004 |
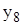 | 0,911 | -0,632 | -0,446 | 1,105 | 0,812 | 1,562 | 0,053 |
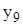 | 1,134 | -0,054 | 0,003 | 1,794 | 1,235 | 2,535 | 0,948 |
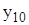 | 1,312 | 0,484 | 0,059 | 2,003 | 1,412 | 3,245 | 1,991 |
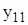 | 1,549 | 0,932 | 0,135 | 2,951 | 1,441 | 3,159 | 2,953 |
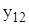 | 1,672 | 1,567 | 0,534 | 4,102 | 1,461 | 3,899 | 3,793 |
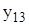 | 2,003 | 2,344 | 0,844 | 4,509 | 1,492 | 3,631 | 4,004 |
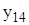 | 2,201 | 2,341 | 1,002 | 4,903 | 1,476 | 3,242 | 5,031 |
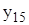 | 2,004 | 1,452 | 1,115 | 5,013 | 1,352 | 3,240 | 5,009 |
Окончание таблицы 7.2.
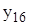 | 1,945 | 0,962 | 1,009 | 4,609 | 1,094 | 3,246 | 4,031 |
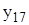 | 1,021 | 0,602 | 0,896 | 3,209 | 0,712 | 2,183 | 3,011 |
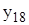 | 0,098 | 0,323 | 0,655 | 2,901 | 0,230 | 1,701 | 0,091 |
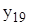 | -0,032 | -0,481 | 0,121 | 1,954 | -0,396 | 0,594 | -0,543 |
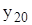 | -0,453 | -0,425 | 0,005 | 0,951 | -0,325 | -0,044 | -0,944 |
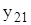 | -0,962 | -1,822 | -0,335 | -0,66 | -0,624 | -1,434 | -2,204 |
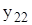 | -1,452 | -2,454 | -1,965 | -0,103 | -0,936 | -2,999 | -2,951 |
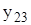 | -2,342 | -3,035 | -2,766 | -2,101 | -1,260 | -3,953 | -6,945 |
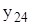 | -2,546 | -3,652 | -4,531 | -3,025 | -1,597 | -4,005 | -6,949 |
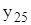 | -2,743 | -4,253 | -4,975 | -3,135 | -1,947 | -4,973 | -7,654 |
Задачи
Задача 1.Определить плотность 5% раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 3,073 | 3,982 | 4,883 | 6,661 | 5,754 |
| r (г/см3) | 1,015 | 1,020 | 1,025 | 1,035 | 1,030 |
Задача 2.Определить плотность 16 % раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 9,259 | 10,97 | 14,31 | 17,58 | 20,79 |
| r (г/см3) | 1,050 | 1,060 | 1,080 | 1,10 | 1,120 |
Задача 3.Определить плотность 42% раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 39,8 | 40,58 | 42,14 | 44,48 | 47,63 |
| r (г/см3) | 1,245 | 1,250 | 1,260 | 1,275 | 1,295 |
Задача 4.Определить плотность 63% раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 60,67 | 61,69 | 65,84 | 68,1 | 70,39 |
| r (г/см3) | 1,370 | 1,375 | 1,395 | 1,405 | 1,415 |
Задача 5.Определить плотность 18,5% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 17,43 | 18,09 | 20,08 | 21,38 | 22,67 |
| r (г/см3) | 1,120 | 1,125 | 1,140 | 1,150 | 1,160 |
Задача 6.Определить плотность 27% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 25,84 | 27,72 | 28,33 | 30,18 | 34,42 |
| r (г/см3) | 1,185 | 1,200 | 1,205 | 1,22 | 1,255 |
Задача 7.Определить плотность 49% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 47,39 | 48,45 | 51,52 | 59,24 | 54,97 |
| r (г/см3) | 1,370 | 1,380 | 1,410 | 1,390 | 1,445 |
Задача 8.Определить плотность 67,5% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 61,54 | 63,36 | 66,03 | 68,23 | 70,39 |
| r (г/см3) | 1,515 | 1,535 | 1,565 | 1,590 | 1,615 |
Задача 9.Определить плотность 84% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 79,37 | 80,7 | 85,16 | 83,06 | 89,23 |
| r (г/см3) | 1,720 | 1,735 | 1,780 | 1,760 | 1,810 |
Задача 10.Определить плотность 96% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 84,08 | 85,74 | 92,51 | 95,72 | 94,32 |
| r (г/см3) | 1,770 | 1,785 | 1,826 | 1,835 | 1,832 |
Задача 11.Определить плотность 18,5% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 17,43 | 18,09 | 20,08 | 21,38 | 22,67 |
| r (г/см3) | 1,120 | 1,125 | 1,140 | 1,150 | 1,160 |
Задача 12.Определить плотность 16 % раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 9,259 | 10,97 | 14,31 | 17,58 | 20,79 |
| r (г/см3) | 1,050 | 1,060 | 1,080 | 1,10 | 1,120 |
Задача 13.Определить плотность 5% раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 3,073 | 3,982 | 4,883 | 6,661 | 5,754 |
| r (г/см3) | 1,015 | 1,020 | 1,025 | 1,035 | 1,030 |
Задача 14.Определить плотность 84% раствора серной кислоты при температуре 20°С по следующим данным:
| x (%H2SO4) | 79,37 | 80,7 | 85,16 | 83,06 | 89,23 |
| r (г/см3) | 1,720 | 1,735 | 1,780 | 1,760 | 1,810 |
Задача 15.Определить плотность 63% раствора азотной кислоты при температуре 20°С по следующим данным:
| x (% HNO3) | 60,67 | 61,69 | 65,84 | 68,1 | 70,39 |
| r (г/см3) | 1,370 | 1,375 | 1,395 | 1,405 | 1,415 |
Порядок выполнения лабораторной работы.
1. Подобрать эмпирическую зависимость вида 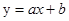 .
.
2. Подобрать эмпирическую зависимость вида 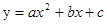 .
.
3. Построить диаграмму рассеивания и графики полученных зависимостей на одном поле.
4. Выбрать лучшую из найденных зависимостей.
5. Подобрать в автоматическом режиме еще любые три зависимости, включая логарифмическую, и выбрать из низ наилучшую.
6. Проанализировать полученные результаты.
Контрольные вопросы.
1. Для чего служит метод наименьших квадратов?
2. На основании чего осуществляется выбор вида аналитической зависимости?
3. Почему метод нахождения коэффициентов аналитической зависимости называется методом наименьших квадратов?
4. Как составить систему нормальных уравнений для нахождения коэффициентов аналитической зависимости?
5. Как можно проверить правильность полученной в результате расчетов формулы?
6. Для чего служит линия тренда?
7. Что характеризует показатель достоверности аппроксимации R2?
